题目是朋友问我有没有思路,然后就做了这道题。我本身不是打竞赛的,所以有些地方可能不是那么精准。
思路:
因为这个是计算几何的问题。在此之前我并没有接触过。一开始是想先想出一个暴力解,然后在此的基础之后优化。
但显然,我总不能按照角度,进行暴力解之类云云的。。。
所以我就想能不能猜一猜答案 : 二分法。
首先 你拿到箱子的时间不可能比你走到离你位置最近的传送带边缘时间还要短。
然后时间不可能比你走到离你位置最近的传送带边缘时间再从后面追着箱子然后拿到箱子的时间还要长
那么就会有一个很明显的范围在这里。我每次只需要猜中间时间是否能够拿到箱子(验证方法)。
因为此时我猜测的时间是固定的,那么箱子在花费这个时候后一定会在一个位置上。
那么对此我就可以分为三类:
1) 我无法在时间 0 - t 内到达那个点
2) 我正好可以在 t 时到达那个店
3) 我可以在小于 t 的时间内到达那个点
那么我现在只要知道我能不能在这个时间内到达它会到达的点就可以了。
在此其实还要解决一个问题,那就是 : 假设正确答案是T,那么在 t > T时一定能在 行李箱行恰好走了t时停留的位置上 花费小于等于t的时间拿到箱子 拿到箱子(因为我们的验证就是建立于此)。
这一步极其重要,因为如若不满足,则我们无法成立二分的一个重要的条件 : 在t < T时 都不能拿到箱子,在 t >= T时都能拿到箱子。
因为存在条件 : 0 < Vl < Vp < 10000 ( Vl ,Vp分别代表行李箱和人的速度),那么即使人先到达T时箱子到达的地点,再沿着边和行李箱同方向走也一定能在t内到达t时箱子到达的地点。
那么接下来我们只要在不越过传送带的前提下判断在走最短路径的情况下是否能够到达 t 时箱子到达的地点。
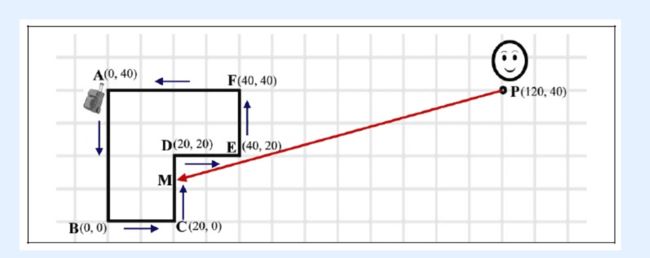
 接下里我们以此图为例子。红点是终点,它处于一个线段中间,而传送带外很多线相交的就是起点。
接下里我们以此图为例子。红点是终点,它处于一个线段中间,而传送带外很多线相交的就是起点。
首先,我们特别标明两个点 : A, B 于图中。也就是于起点作无数条线段,至少会有两点与多边形相交,这就是A , B点。
那么我们所作的无数条线段可以分为三类 :
1) 在A - B 两点之内
2)与 A或 B 相交
3) 在A, B 之外
如若我们选择1),例如图中的c路径,根据三角形定理 : 两边之和大于第三边。因为c路径不能直接越过传送带找重点,所以一定要与 a 或 b路径形成的线段相交, 即 : c路径到达 a路径 交点 一定会比直接从 a 路径 到达这个交点的路程更长! b路径同理。所以我们排序1)
如若我们选择3),那么我们仍然要经过a或b路径(同上)。所以我们派出3)
那么最终,我们一开始的出发点一定会是a,b路径方向之中的一个,且最少要到达A或B点(因为如若不到达A 或 B点 仍然要面对从此时的点到达终点最短路径问题,而A B 仍然有一点会是交点,而另一边虽然改变,但是是不可能选择的,因为这样一定会比直接往另一边慢,即两点之间直线最短)。
那么我们很巧妙地将问题转换为了: 从A点或者B点到终点最短路径。
为何不必考虑越过起点到A或B的线段之外部分的点?
因为我们只需要考虑A点或B点到终点,而之外的点是否会在最短路径内,这个可能性已经包含在当前问题内了!
那么很明显,我们只需要再作切线就行了,例如我们目前选择了A,那么我们的一个切线是终点附近,一个是在A,B之间的。我们无须离A,B之间的那个点。因为我们不可能走回头路。
我们只需要直接走到终点附近那个凸点就可以了。至于为什么不往外走,同上。
那么如若我们目前选择了B点呢?
我们重复之前想法,先找到两个切点,然后抛弃回头路。
我们可以很明显地看到我们所有可能性的点都会是“最凸点”,就是作无数条切线与之相切的那两个点之中的一个。而如若是凹的,那么我们不必考虑。
这么我们可以总结一个结论 : 我们只需要分两个方向,不断行走在对应最凸点上,直到我们到达与终点相邻的最凸点,我们直接到达终点即可!
后续还会有代码更新。。。