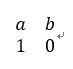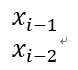矩阵快速幂以及快速幂的10倍增形式

之前听说过很多次矩阵快速幂但是这一次是第一次去学习这个算法，首先从最基本的矩阵快速幂模板开始讲起（因为这一题直接套用二倍增的模板的话会T）

矩阵的乘法在线性代数里都有学过，这里就不讲了。

矩阵的乘法这里有两种写法，一种是以函数的形式，还有一种就是通过重载运算符，这里我用的是函数的形式。

 1 Mat Mul(Mat x,Mat y)
 2 {
 3     Mat a;
 4     for(int i=1;i<=n;i++)//初始化矩阵
 5     for(int j=1;j<=n;j++)
 6     a.m[i][j]=0;
 7     for(int i=1;i<=n;i++)//计算矩阵
 8     for(int j=1;j<=n;j++)
 9     for(int k=1;k<=n;k++)
10     a.m[i][j]=(a.m[i][j]%mod+x.m[i][k]*y.m[k][j]%mod)%mod;
11     return a;
12 }

 然后只要把快速幂中的乘法改成矩阵的乘法就可以了

 1 Mat Mode(Mat a,ll b)//快速幂
 2 {
 3     Mat ans=e;
 4     while(b>0)
 5     {
 6         if(b%2==1)
 7         ans=Mul(ans,a);
 8         b/=2;
 9         a=Mul(a,a);
10     }
11     return ans;
12 }

 那么已经会了矩阵的快速幂，那么能拿来干什么呢，下面我们看一下矩阵快速幂的应用

最主要的应用就是矩阵快速幂可以通过把不同的数放在不同的位置来构建矩阵从而用来求解递推式

2019牛客多校第五场B题

看一下这个题目   题目告诉我们x_i=a*x_i-1+b*x_i-2

告诉我们x₀,x₁,a,b和n让我们求出x_n的大小

那我们可以构建出一个的矩阵与的一个矩阵的递推式。

(不是很明白的人最好自己先想一下这两个矩阵是怎么来的，因为我刚开始看的时候想了好半天，还构建错了好多次，一定要自己先思考再往下看)

我这里把这两个矩阵的递推过程模拟出来（例如求x₃）字丑不要介意

我们设前面那个常数矩阵为T，也叫转移矩阵，那么我们只要得到Tⁿ之后，再加一步计算就可以得到答案了。这个时候就可以用到上面说的矩阵快速幂了。

但是！！！！

这一题有一点不同，这一题的n的范围是10的10⁶次方，那么如果只用模板的二倍增的话，不仅会T，而且用什么来存这么大的数呢，所以这里也是根据题解说的，采用10倍增的方式快速幂，下面我们来说一下如何对大数n次方进行10倍增的快速幂。

比如说我们要求2¹²³⁴⁵，那么我们可以把12345分成10000，2000，300，40，5，那么第一次我们从1快速幂到5，第二次我们以10为基础，快速幂到40，第三次我们以100为基础，快速幂到300，以此类推，这样我们就可以比二进制更快的算出来结果。

 1 #include 
 2 #include 
 3 #include <string>
 4 #include 
 5 #include 
 6 #include 
 7 #include 
 8 #include 
 9 #include <string.h>
10 
11 #define ll long long
12 using namespace std;
13 ll x0,x1,a,b,mod;
14 char n[1000005];
15 struct Mat
16 {
17     ll mat[2][2];
18     void init()//初始化为单位矩阵
19     {
20         for(int i=0;i<=1;i++)
21         for(int j=0;j<=1;j++)
22         mat[i][j]=0;
23         for(int i=0;i<=1;i++)
24         mat[i][i]=1;
25     }
26 };
27 Mat Matpow(Mat a,Mat b)//矩阵的乘法
28 {
29     Mat ans;
30     for(int i=0;i<=1;i++)
31     for(int j=0;j<=1;j++)
32     ans.mat[i][j]=0;
33     for(int i=0;i<=1;i++)
34     for(int j=0;j<=1;j++)
35     for(int k=0;k<=1;k++)
36     {
37         ans.mat[i][j]+=a.mat[i][k]*b.mat[k][j]%mod;
38         ans.mat[i][j]%=mod;
39     }
40     return ans;
41 }
42 Mat pow(Mat a,ll b)//基本的快速幂，把乘法改成矩阵乘法即可
43 {
44     Mat ans;
45     ans.init();
46     while(b>0)
47     {
48         if(b%2==1)
49         ans=Matpow(ans,a);
50         b/=2;
51         a=Matpow(a,a);
52     }
53     return ans;
54 }
55 int main()
56 {
57     //freopen("C:\\Users\\16599\\Desktop\\in.txt","r",stdin);
58     scanf("%lld%lld%lld%lld",&x0,&x1,&a,&b);
59     scanf("%s%lld",n,&mod);
60     Mat res,ans;
61     ans.init();
62     res.mat[0][0]=a;res.mat[0][1]=b;res.mat[1][0]=1;res.mat[1][1]=0;//构建转移矩阵
63     for(int i=strlen(n)-1;i>=0;i--)
64     {
65         ans=Matpow(ans,pow(res,n[i]-'0'));//计算当前位的值
66         res=pow(res,10);//将转移矩阵扩大10倍，达到优化效果
67     }
68     ll xn=(ans.mat[1][0]*x1%mod+ans.mat[1][1]*x0%mod)%mod;//得到xn
69     printf("%lld\n",xn);
70     return 0;
71 }