姓名:何承勇
学号:16050510005
原文链接:https://blog.acolyer.org/2016/04/21/the-amazing-power-of-word-vectors/
转载自:http://www.jianshu.com/p/6c4ce9ef66aa,有删改
【嵌牛导读】:将词用“词向量”的方式表示可谓是将Deep Learning算法引入NLP领域的一个核心技术。大多数宣称用了Deep Learning的论文往往也用了词向量。
【嵌牛鼻子】:深度学习、词向量、word2vec
【嵌牛提问】:词向量在深度学习中是如何运作的?
【嵌牛正文】:
今天的帖子,我收集的材料源于五篇论文。本次的主题是“word2vec”,主要是总结了Google公司的Mikolov等人关于词向量的工作(以及你可以用它做什么)。论文分别是:
·Efficient Estimation of Word Representations in Vector Space – Mikolov et al. 2013
·Distributed Representations of Words and Phrases and their Compositionality – Mikolov et al. 2013
·Linguistic Regularities in Continuous Space Word Representations – Mikolov et al. 2013
·word2vec Parameter Learning Explained – Rong 2014
·word2vec Explained: Deriving Mikolov et al’s Negative Sampling Word-Embedding Method – Goldberg and Levy 2014
第一篇论文中,我们学习到了词向量方面的连续Bag-of-Words模型和连续 Skip-gram模型(我们马上将谈到词向量)。第二篇文章中,我们充分展示了词向量的魅力,并优化了Skip-gram模型(层次softmax和负采样)。另外,还将词向量的概念和性质推广到短语中。第三篇文章描述了基于词向量的向量推理,并介绍了著名的“King – Man + Woman = Queen”的例子。最后的两篇论文是其他人对Milokov论文的一些思想进行了深入的解释。
可以在Google Code上找到word2vec的实现 。
什么是词向量
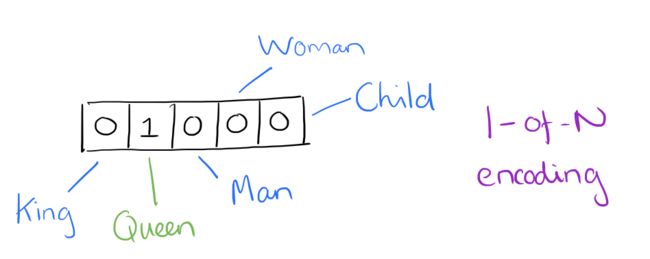
从某种意义上来讲,词向量只是简单的权重向量。在简单的一位有效编码方式下,向量中每一个元素都关联着词库中的一个单词,指定词的编码只是简单的将向量中相应元素设置为1,其他的元素设置成0。
假设我们的词汇只有五个词:King, Queen, Man, Woman, 和 Child。 我们可以将单词“Queen”编码为:
如果使用这样的编码,除了等量的运算,我们无法对词向量做比较。
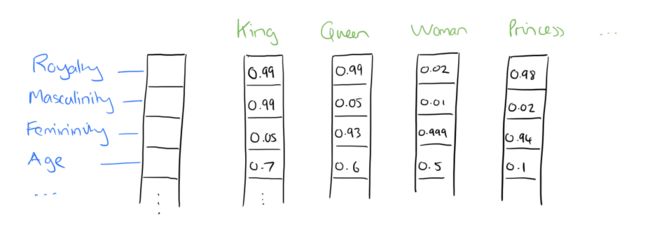
在word2vec中,词的分布式表征被使用。在向量维数比较大(比如1000)的情况下,每一个词都可以用在元素的分布式权重来表示。因此,一个词的表示形式在向量中的所有元素中传播,每一个元素都对许多词的定义有影响,而不是简单的元素和词之间的一对一映射。如果我标记了假象词向量的维度(当然,在算法中没有这样的预分配标签),它可能看起来是这样的:
这样的向量来以某种抽象的方式来表示一个词的“意义”,接下来我们可以看到,只是通过简单地检查一个大的语料库,它可能以一个令人惊讶的方式学习词向量并能够捕捉到的词汇之间的关系。当然,我们也可以把向量作为神经网络的输入。
词向量推理
事实上我们发现,被学习的词表征用一种非常简单的方式捕捉有意义的语法和语义规律。具体来说,对于有特定关系的词组,语法规律可以看作固定的向量偏移。举个例子,我们把单词i的向量表示为xi,如果我们关注单复数的关系,我们可以发现xapple–xapples≈xcar–xcars, xfamily–xfamilies≈ xcar–xcars等这样的规律。更令人惊讶的是,各种语义关系也是一样,正如SemEval 2012年测量关系相似性的工作所揭示的那样。
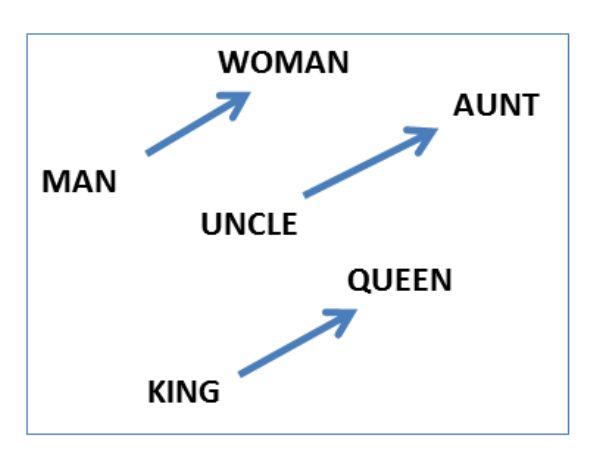
向量非常适用于解决类比的问题,比如a对b来说正如c对什么这种形式的问题。举个例子,使用基于余弦距离的向量偏移可以解决男人对女人来说正如叔叔对什么(婶婶)的问题。
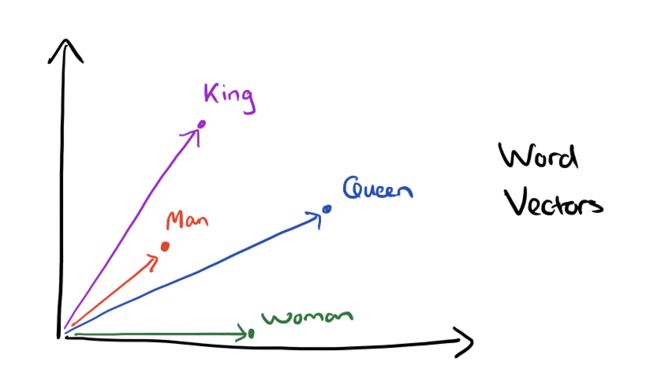
举个例子,下图表示性别关系的三对词的矢量偏移:
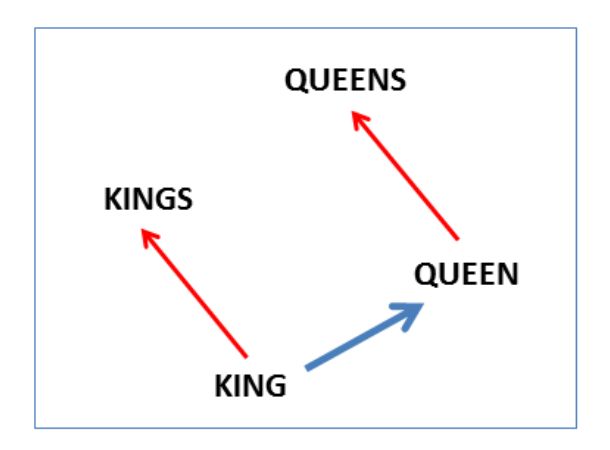
下图表示单复数关系:
这类型的向量可以回答“King – Man + Woman = ?”的问题并得出结果“Queen”。在没有额外提供信息的情况下,仅仅是通过浏览大量的语义资料(正如我们即将见到的)获取这样的知识是非常令人激动的。
稍微令人惊讶的是,词表征的相似性超过了语法规律。它仅仅是对词向量的简单运算,就能得出如下面例子的vector(“King”) – vector(“Man”) + vector(“Woman”)接近“Queue”的词表征的结果。
King, Man, Queen, 和Woman的向量如下所示:
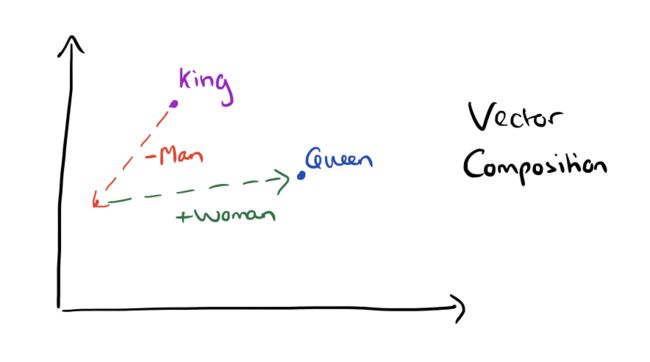
向量合成King – Man + Woman = ?的结果:
这里还有一些用同样技术的实现结果:
这里有国家-首都关系的一个2维的主成分分析预测:
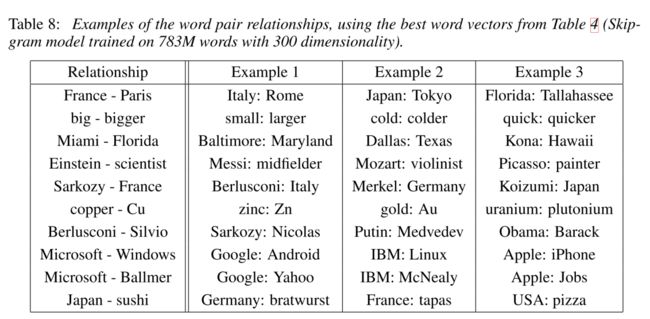
下面是一些类似于“a对b正如c对什么?”这类问题的例子:
我们也可以使用向量元素之外的元素智能来解决诸如“德国+航线”的问题,通过合成向量来获得最终的结果:
有这样语意关系的词向量可以用来改进很多现有的自然语言处理应用比如机器翻译、信息检索和问答系统,甚至会催生出新的创意和应用。
下图展示了基于语法和语义的词关系测试,使用一个skip-gram训练模型得到的640维的词向量可以获得55%的语义准确率和59%的语法准确率。
学习词向量
Mikolov等人并不是第一个使用词的向量表示形式的,但是他们确实减小了计算的复杂性,使在大量数据上学习高维词向量成为可行的。举个例子,“我们已经使用了谷歌新闻语料库进行训练的单词向量。该语料库包含6B词组。我们已经限制了词汇量的100万个最频繁的单词……”。
神经网络语言模型(前馈或递归)的复杂性来自于非线性隐层(S)。
尽管这就是神经网络的魅力所在,我们决定探索更简单的模型,也许精度并不如神经网络,但也可能是更有效的训练更大量数据。
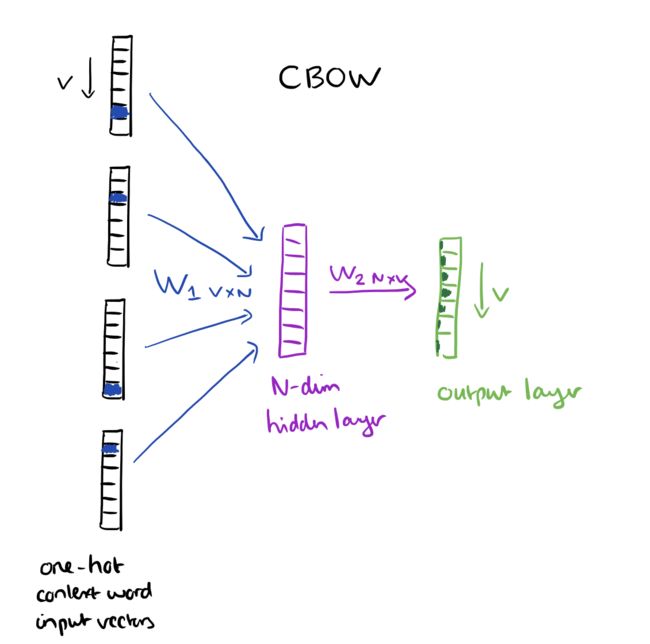
两种新的架构被提出:Continuous Bag-of-Words model和 Continuous Skip-gram model.我们先看Continuous Bag-of-Words(CBOW)。
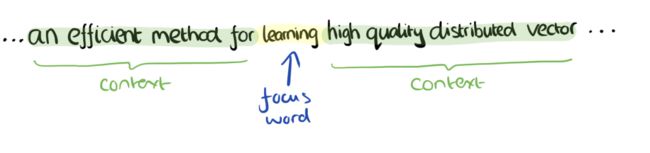
考虑这样一段散文“The recently introduced continuous Skip-gram model is an efficient method for learning high-quality distributed vector representations that capture a large number of precises syntatic and semantic word relationships.”,想象这段文字上有一个滑动窗口,包括当前的词和前后的四个词,具体如下图所示。
上下文词组成了输入层,每一个词都用一位有效编码的方式来表示。如果词汇量是V,这些词都变成V维向量,相应的词被设置成1,其余的为0。下图表示单隐层和一个输出层。
训练的目标是最大限度地观察实际输出词(焦点词)在给定输入上下文且考虑权重的的条件概率。在我们的例子中,给出了输入(“一个”,“有效”,“方法”,“为”,“高”,“质量”,“分布式”,“向量”)我们要最大限度地获得“学习”作为输出的概率。
由于我们的输入向量都是一位有效编码的方式来表示,和权重矩阵W1相乘就相当于简单的选择一行。
如果输入了C个词向量,隐层的激活函数其实就是用来统计矩阵中的热点行,然后处以C来取平均值。
这意味着,隐藏层单元的链接(激活)函数就是简单的线性运算(直接将权重和作为下一层的输入)。
从隐层到输出层,我们用一个权重矩阵W2来为每一个词计算得分,同样,可以使用softmax来计算词的后验分布。
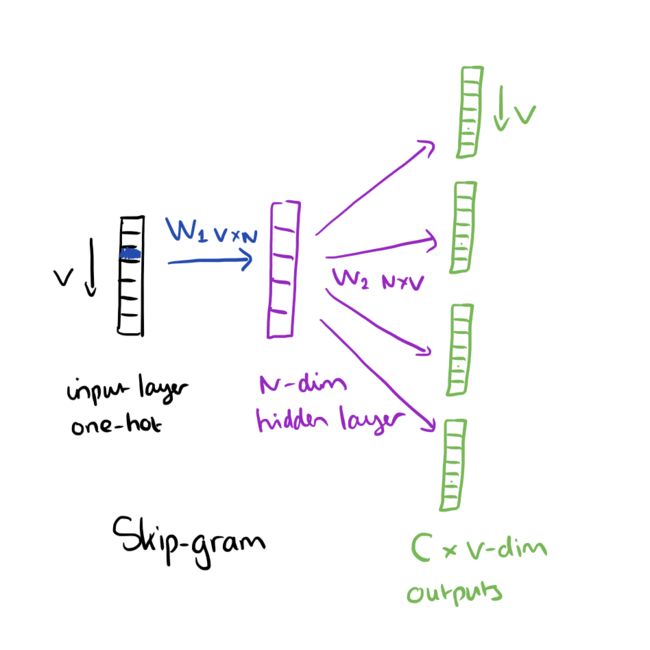
skip-gram和CBOW正好相反,它使用单一的聚焦词作为输入,目标上下文词作为输出,正如下图所示:
正如之前提到的,隐层的激活函数只是权重矩阵W1对应行的简单统计。在输出层,我们输出C个多项式分布。训练的最终目标就是减小输出层所有上下文词的预测错误率。举个例子,如果输入“learn”,我们可能得到在输出层得到“an”, “efficient”, “method”, “for”, “high”, “quality”, “distributed”,“vector”。
优化
在一个训练实例中,为每一个词输出词向量代价是非常大的……
首先从直觉上来看,对每次训练实例中更新的输出向量进行一个数量上的限制是解决这个问题的办法。但是我们提供了两种优雅的方法,一个是基于层次的柔性最大传递函数,另一个就是采样。
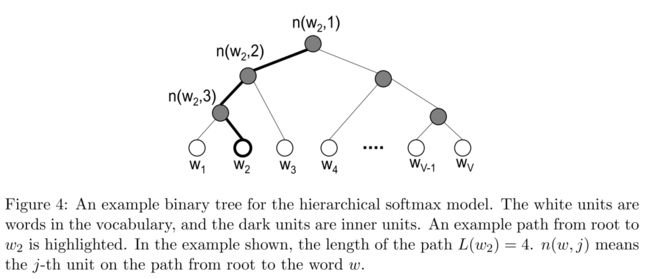
Hierarchical softmax 使用二叉树来表示词汇表中的所有词,每一个词在树中表示为叶子。对于每一个叶,从根到叶存在一个独特的路径,这条路径是用来估计由叶表示的单词的概率。“我们用从根到叶的随机游走的概率来定义这样的概率。”
这样的好处是不用对V个节点一一评估来获得神经网络中的概率分布,而是只用评估log2(V)个节点。在这里我们使用二叉哈夫曼树,因为它给高频词汇赋予更短的编码,这样一来,训练过程就变快了。
负采样的想法很简单,就是每一次迭代我们只更新样本的输出词。目标输出词应该被留在样本中,并且应该被更新,我们还要加入一些(非目标)词作为负样本。“在采样过程中,概率分布是必要的,概率分布选择的灵活性比较大, 一般都根据经验来选择”。
Milokov等人也使用简单的二次采样方向来计量训练集合中比率和频次的不平衡性。(举个例子,“in”,“the”, 和“a”比不常出现的词提供更少的信息)。训练集中的每一个词都有一个丢弃概率,可以用下面的公式表示:
f(wi)表示词wi出现的频率,t是一个阈值,一般来说取10-5附近的数。
原文作者:阿里云云栖社区