NOIP2016提高组 天天爱跑步

（树上差分 + \(LCA\)） \(O(Mlog_2N)\)

---

调了两个小时，最后发现把\(lca\)里的\(y\)写成\(x\)了，当场去世。

首先下几个定义：

1. \(dis[x]\) 为\(x\)到根节点的距离。由于边权都是\(1\)，所以\(dis[x] = dep[x]\)
2. \(LCA(x, y)\) 为 \(x, y\) 的最近公共祖先
3. \(LCA(x, y)\ down\) 为 \(x, y\) 的最近公共祖先在往\(y\)的放下下去一格（这里不懂可以看下面的图）
4. \(ans[x]\) 为这个点的答案
5. 我们称玩家跑的路线为"一条路径"

对于第\(i\)个玩家，发现可以将从\(S_i\)到\(T_i\)的路径分成两条链：

1. \(S_i\) 到 \(LCA(S_i, T_i)\)
2. \(LCA(S_i, T_i)\ down\) 到 \(T_i\) （这里不算\(LCA\)，不然会重复两次 ）

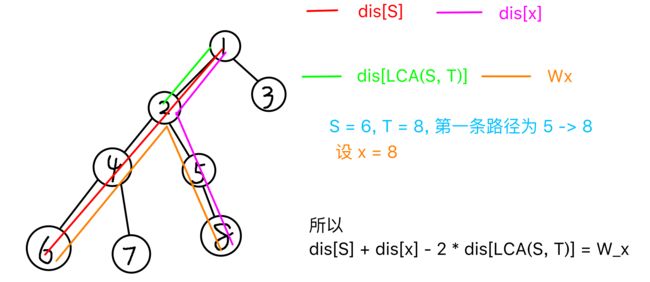
不太理解的同学看这张图，设\(S_i = 6, T_i = 8\)。其中$ LCA(6, 8) down = 5$

我们从每条路线对答案的贡献来看，进行分类讨论（最后的答案就是两个之和）：

从起点出发，终点在第一条链上（上升链）：

考虑一个玩家\(i\)对答案的贡献：

这条玩家的起点为\(S_i\) ，终点为 \(LCA(S_i, T_i)\)。

考虑它对答案的贡献只存在于这条链上（因为它只走过这条链上的点）：

设在这条链上存在一点\(x\)，且到\(x\)点刚好为\(W_x\)秒，则有：

\(dis[S_i] - dis[x] = W_x\)

转换一下（把能从\(x\)直接得到的放在一边，需要统计的放在另一边）：

\(dis[x] + W_x = dis[S_i]\)

考虑一个点得到的答案：

也就是说，当存在一个路径\(S_y, T_y\)使得：

\(dis[x] + W_x = dis[S_y]\)的时候，就看见了一个人\(ans[x]++\)

---

那我们只要建立一个数组\(d1\) , \(d1[x][a]\) 表示以x为节点的答案统计中， \(a\)这个值出现了多少次。

那么，\(ans[x] = d1[x][W_x]\)

---

但注意了，这条线到 \(LCA(S_y, T_y)\) 会拐弯，\(y\)这个人对 \(LCA(S_i, T_i)\)的上面的节点答案是没有贡献的。

---

我们总结一下：

对于一条线的上升部分的处理，我们需要：

对于\(S_i\) 到\(LCA(S_i, T_i)\) 这条链上的所有点\(b\)，让\(d1[b][dis[S_i]]++\)。

这不就是树上差分吗？

我们还发现\(d1\)的第一维可以滚动掉，然后用一遍\(dfs\)动态维护这个次数。

从起点出发，终点在第二条链上（下降链）：

这里，我们可以用第一条链的思路进行思考，只不过改变一下细节。

考虑一个玩家\(i\)对答案的贡献：

这条玩家的起点为\(LCA(S_i, T_i)\ down\) ，终点为 \(T_i\) 。

考虑它对答案的贡献只存在于这条链上（因为它只走过这条链上的点）：

设在这条链上存在一点\(x\)，且到\(x\)点刚好为\(W_x\)秒，则有：

\(dis[S_i] + dis[x] - 2 * dis[LCA(S_i, T_i)] = W_x\)

转换一下：（把能从\(x\)直接得到的放在一边，需要统计的放在另一边）：

\(W_x - dis[x] = dis[S_i] - 2 * dis[LCA(S_i, T_i)]\)

考虑一个点得到的答案：

也就是说，当存在一个条路径\(S_y,\)使得：

\(W_x - dis[x] = dis[S_y] - 2 * dis[LCA(S_y, T_y)]\)的时候，就看见了一个人\(ans[x]++\)

---

我们建立一个数组\(d2\) , \(d2[x][a]\) 以x为节点的答案统计中， \(a\)这个值出现了多少次。

那么，\(ans[x] = d2[x][W_x]\)

---

我们总结一下：

对于一条线的上升部分的处理，我们需要：

对于\(LCA(S_i, T_i)\ down\) 到 \(T_i\) 的这条链上的所有点\(b\)，让\(d1[b][dis[S_i] - 2 * dis[LCA(S_i, T_i)]]++\)。

同理，我们这里也可以使用树上差分。

这里需要注意的一点是：\(dis[S_i] - 2 * dis[LCA(S_i, T_i)]\) 可能是负数，为了不让数组越界，我们可以加一个偏移量

注意事项

这种特殊（需要二维数组，滚动数组优化后）的树上差分如下：

1. 存下所有点的操作序列。
2. 每次到一个点的时候，把它的所有操作执行一遍。
3. 注意一个特殊的点，这里可能会统计掉其他子树（旁支），所以只需开始进入的时候存一个，回溯的时候存一个，两数相减即为答案。

代码实现（我用的是倍增求LCA）：

#include 
#include 
#include 
using namespace std;
typedef pair PII;
const int N = 300005, M = N << 1, L = 19;
int n, m, fa[N][L], dis[N];

//d1的下表值域是(0 ~ 2n)的
int d1[N << 1], d2[N << 1], ans[N], w[N];

//op1, op2 分别是 d1, d2 的操作序列
//Pair(下表的值，要加的次数)
vector op1[N], op2[N]; 

//链式前向星
int head[N], numE = 0;
struct Edge{
    int next, to;
}e[M];
void addEdge(int from, int to){
    e[++numE].next = head[from];
    e[numE].to = to;
    head[from] = numE;
}
//预处理dfs
void dfs_(int u, int last){
    fa[u][0] = last;
    for(int i = 1; fa[u][i - 1]; i++)
        fa[u][i] = fa[fa[u][i - 1]][i - 1];
    for(int i = head[u]; i; i = e[i].next){
        int v = e[i].to;
        if(v == last) continue;
        dis[v] = dis[u] + 1;
        dfs_(v, u);
    }
}
//倍增求LCA
int lca(int x, int y){
    if(dis[x] < dis[y]) swap(x, y);
    for(int i = L - 1; ~i; i--)
        if(dis[x] - (1 << i) >= dis[y])
            x = fa[x][i];
    if(x == y) return x;
    for(int i = L - 1; ~i; i--)
        if(fa[x][i] != fa[y][i])
            x = fa[x][i], y = fa[y][i];
    return fa[x][0];
}
//添加操作序列
void update(int s, int t){
    int p = lca(s, t);
    op1[s].push_back(make_pair(dis[s], 1));
    op1[fa[p][0]].push_back(make_pair(dis[s], -1));
    op2[t].push_back(make_pair(dis[s] - 2 * dis[p] + n, 1));
    op2[p].push_back(make_pair(dis[s] - 2 * dis[p] + n, -1));
}
//最后一遍dfs求答案
void dfs(int u, int last){
    //v1, v2 就是我们寻找的值
    int v1 = w[u] + dis[u], v2 = w[u] - dis[u] + n;
    int res1 = d1[v1], res2 = d2[v2];
    for(int i = head[u]; i; i = e[i].next){
        int v = e[i].to;
        if(v == last) continue;
        dfs(v, u);
    }
    //加入操作
    for(int i = 0; i < op1[u].size(); i++)
        d1[op1[u][i].first] += op1[u][i].second;
    for(int i = 0; i < op2[u].size(); i++)
        d2[op2[u][i].first] += op2[u][i].second;
    ans[u] = (d1[v1] - res1) + (d2[v2] - res2);
}
int main(){
    scanf("%d%d", &n, &m);
    for(int i = 1; i < n; i++){
        int u, v; scanf("%d%d", &u, &v);
        addEdge(u, v); addEdge(v, u);
    }

    for(int i = 1; i <= n; i++)
        scanf("%d", w + i);
    dfs_(1, 0);
    for(int i = 1; i <= m; i++){
        int s, t; scanf("%d%d", &s, &t);
        update(s, t);
    }
    dfs(1, 0);
    for(int i = 1; i <= n; i++)
        printf("%d ", ans[i]);
    return 0;
}

鸣谢：

1. 秦dalao的讲义
2. MrWriter 画图软件
3. SM.MS 的图床