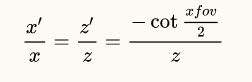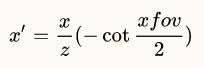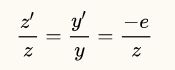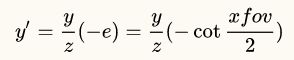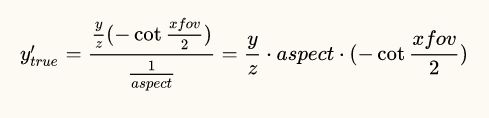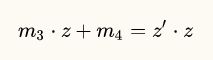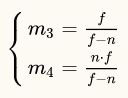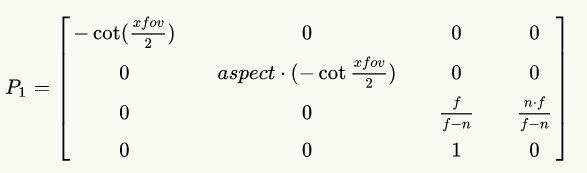书上和网上有很多透视变换的例子，但是其缺点是只讨论一种情况，无法将不同的情况关联起来，因此整理一篇文章，希望可以把透视变换的相关东西都联系起来。

透视变换

透视变换，就是用一个矩阵（透视变换矩阵）将整个场景转换到齐次裁剪空间之中。所谓的齐次裁剪空间，是一个特殊的空间，它的作用就是让渲染管线可以对这个空间中一定范围内的物体保留，超出范围的物体剔除，如果有阶段表面的情况，还要生成新的顶点数据。
齐次裁剪空间通常有两种，两种齐次裁剪空间的x和y坐标范围都是[-1,1]，但是z坐标的范围不同，一种是[0,1]，一种是[-1,1]。很多书上，网上的教程都会说DX的齐次裁剪空间是[0,1]的那种，而OpenGL的裁剪空间是[-1,1]的那种。不过到底事实是什么样的，我们还得试过之后才知道。
为了在计算机中模拟人眼看东西的状态，我们想出了这样的一个模型：把人眼固定在相机空间的原点，然后从原点定义一个四棱锥，表示人眼可以看到的范围，就像下面这张图一样：

这个四棱锥就被称为视景体。除此之外，对于离眼睛太近的物体我们看不到，太远的物体同样也看不到，所以我们可以选取一定范围内的物体显示出来，这样可以节省渲染时间。那么多近的物体不显示，多远的物体不显示呢？这个没有定论，经常使用n和f表示这两个距离，比n近的物体不显示，比f还远的物体不显示。这两个面就把视景体截断成一个四棱台，这个四棱台里的物体会被绘制，而在外面的不会。

接着，我们就可以来推导这个透视变换矩阵了。此时我们是在相机中间中，并且假设相机空间是一个右手坐标系。

水平视场角

下图是从视景体的上方垂直看下去的图，就像是三视图一样。图中，三角形的顶边就是投影平面。

参数说明：为了计算方便，我们取特殊的投影平面，它的x坐标区间是[-1,1]，这个坐标区间刚好可以直接当成齐次裁剪空间的坐标。如图中所示，投影平面距离原点的距离为e，注意这是距离，不是投影平面的z坐标，这个e有时也被称为相机的焦距。这样，左锥面和右锥面形成的夹角为xfov，称为水平视场角。

水平视场角，英文名是horizontal angle of view，但是通常，我们会把视场角和视野混用，视野的英文是field of view，所以我就用xfov（x-axis field of view）来表示水平视场角。

可以看到，距离e满足
再来看看垂直方向上：

垂直方向与水平方向类似，投影平面的纵横比（宽除以高）用aspect表示，这个比值通常是16：9，就是我们显示器的宽高比。所以，投影平面的y坐标范围为[-1/aspect, 1/aspect]。如图中所示，垂直视场角

计算投影后的x坐标

原始的顶点是v，投影之后的顶点是v'，根据相似三角形原理，我们可以列出下面的等式：

求解x'得：

接着计算y'的值。

如上图所示，同样使用相似三角形的公式来计算：

于是

到这里，y'的计算还没有结束，最关键的一步来了！上述的推导成立的前提是，y的投影面是[-1/aspect, 1/aspect]，而齐次裁剪空间中，y的取值范围必须是[-1,1]，所以，最后一步是，将上述计算出来的y'值除以1/aspect，得出的结果才是齐次裁剪空间中真正的y值：

转换之前的坐标记为(x, y, z, 1)，转换之后的坐标就是(x', y', z', 1)，将之间计算的结果代入得到转换之后的坐标是

在齐次坐标系统中，点(x, y, z, 1)和点(cx, cy, cz, c)表示的是同一个点，如果这个c不是0的话。利用这个性质，我们可以对上述坐标乘以一个z得到如下的形式

列出转换矩阵表示这个转换过程

转换矩阵中有四个参数没有确定，我们需要把这四个参数解出来。先来思考一下，对z进行投影，这和x,y坐标有没有关系？显然没关系，所以m1和m2的值肯定是0。接下来考虑m3和m4，我们可以列出下面的方程

两边除以z得到

接着，我们说过齐次裁剪空间的z坐标范围有两种，一个是[0,1]，一个是[-1,1]，我们先计算[0,1]。这种转换，近裁剪面（n）转换到0，远裁剪面（f）转换到1，于是我们将坐标代入（注意我们所说的裁剪面n和f是距离）得到方程组

解方程组得到的结果是

将结果代入到转换矩阵里，我们就能得到最终的转换矩阵：

投影矩阵有很多变种，嗯，多到头晕的变种。比如，之前我们为了方便计算，对转换后的坐标值乘以了一个z得到的

显然，我可以不乘z，如果我乘以一个-z得到的结果会是什么呢？

用这个结果去推导投影矩阵，得到的结果是：

很明显，P2 = -P1。这两个矩阵效果都一样吗？事实是， 不一样！P1是一个无效的透视矩阵，P2才是有效的矩阵。这里涉及到裁剪的相关原理。

透视矩阵会把所有的顶点都转换到齐次裁剪空间中，为啥叫齐次裁剪空间？因为在这个空间中，会发生裁剪的操作。为啥是齐次？因为这个空间中的点，w坐标不是1，而是z或者-z。裁剪空间要做的第一件事，就是把w坐标小于0的顶点都剔除。而我们的z坐标，是一个小于0的值！所以，如果你用P1作为透视矩阵，那么你无法看到任何东西，因为它们都被剔除掉了。不信？试试~

推导这么复杂，写成代码就很简单了，只要把结果赋值就好了。

float cFov = 1.f / tanf(xfov / 2);
result.m[0][0] = cFov;
result.m[1][1] = aspect * cFov;
result.m[2][3] = -1;
result.m[2][2] = far / (near - far);
result.m[3][2] = near * far / (near - far);

代码的矩阵是P2矩阵的转置，因为这种数据格式传递给渲染管线的时候计算方便。运行测试场景，得到的结果是：

另一个齐次裁剪空间

之前我们首先的齐次裁剪空间的z范围是[0,1]，那么如果它的范围是[-1,1]，又会是什么结果呢？下面我们来尝试推导[-1,1]的投影矩阵，这个不难，只有最后转换z坐标的时候有区别，我们以乘以-z为基础来推导。
$\begin{bmatrix}\cot({\frac{xfov}{2}}) && 0 && 0 && 0\\ 0 && aspect·(\cot{\frac{xfov}{2}}) && 0 && 0\\ m_1 && m_2 && m_3 && m_4\\ 0 && 0 && -1 && 0\end{bmatrix}·\begin{bmatrix}x \\ y \\ z \\ 1\end{bmatrix}=\begin{bmatrix} x·(\cot{\frac{xfov}{2}})\\ y·aspect·(\cot{\frac{xfov}{2}})\\ -z·z'\\ -z \end{bmatrix}$
首先，m1和m2还是0，因为x坐标和y坐标对z投影之后的坐标值没有影响。然后，列出z坐标转换公式：

两边除以-z

现在，我们要把近裁剪面转换成-1，远裁剪面转换成1，列出方程：

求得

最后的转换矩阵是：
$\begin{bmatrix}\cot({\frac{xfov}{2}}) && 0 && 0 && 0\\ 0 && aspect·(\cot{\frac{xfov}{2}}) && 0 && 0\\ 0 && 0 && \frac{n + f}{n - f} && \frac{2nf}{n - f}\\ 0 && 0 && -1 && 0\end{bmatrix}$
再用代码实现：

float cFov = 1.f / tanf(xfov / 2);
result.m[0][0] = cFov;
result.m[1][1] = aspect * cFov;
result.m[2][3] = -1;
result.m[2][2] = (near + far) / (near - far);
result.m[3][2] = (2 * near * far) / (near - far);

应用这个投影矩阵，得到的结果是：

没有半毛钱区别！

上面两张图是OpenGL下运行的结果，下面两张图是D3D12下运行的结果：

D3D12 z区间为[0,1]

D3D12 z区间为[-1,1]

可以看到，上面两张图也没啥区别。而对比OpenGL和D3D12的图会发现，OpenGL中显示的物体稍微偏上了一点，为什么会产生这种效果，笔者也不清楚。

如果不用fov，还能用什么参数计算投影矩阵？

在《3D游戏与计算机图形学中的数学方法》一书和《Real Time Rendering 4th Edition》一书中，提供了一种不用fov的方法。这个方法是这样的：
首先确定投影平面的位置，令投影平面正好位于近裁剪面处，它与观察点之间的距离为n，所以其z坐标就是-n。然后，这个投影平面的x范围是[l, r]，y范围是[b, t]。先通过相似原理列出一个点(x, y, z, 1)投影到上述投影平面上之后的x，y坐标，令投影后的坐标为(x', y', z', 1)：

同理

现在，我们来计算假如投影平面上有一点(x', y')，要将其坐标映射到[-1,1]区间，计算公式是什么样的？
因为投影平面上x坐标取值范围是[l, r]，我们可以通过x'到l的距离占(r - l)的比例来映射:

要将这个范围转换到[-1,1]，只需要将这个范围翻倍，然后左移一个单位的距离就可以，即：

同理

将x'和y'的式子代入到x''和y''的公式中

转换后的点为

老规矩，乘以-z

列出矩阵
$\begin{bmatrix}\frac{2n}{r-l} && 0 && \frac{r+l}{r-l} && 0\\ 0 && \frac{2n}{t-b} && \frac{t+b}{t-b} && 0\\ 0 && 0 && m_3 && m_4\\ 0 && 0 && -1 && 0\end{bmatrix}·\begin{bmatrix}x \\ y \\ z \\ 1\end{bmatrix}=\begin{bmatrix} \frac{2n}{r-l}(x)+\frac{r+l}{r-l}z \\ \frac{2n}{t-b}(y)+\frac{t+b}{t-b}z \\ (-z)·z''\\ -z \end{bmatrix}$
m3和m4的计算和上面一样，我们直接写出结果就行。对[0,1]区间是
$\begin{bmatrix}\frac{2n}{r-l} && 0 && \frac{r+l}{r-l} && 0\\ 0 && \frac{2n}{t-b} && \frac{t+b}{t-b} && 0\\ 0 && 0 && \frac{f}{n-f} && \frac{nf}{n - f}\\ 0 && 0 && -1 && 0\end{bmatrix}$
对[-1,1]区间是
$\begin{bmatrix}\frac{2n}{r-l} && 0 && \frac{r+l}{r-l} && 0\\ 0 && \frac{2n}{t-b} && \frac{t+b}{t-b} && 0\\ 0 && 0 && \frac{n + f}{n - f} && \frac{2nf}{n - f}\\ 0 && 0 && -1 && 0\end{bmatrix}$
接着我们用代码来实现这个投影矩阵：

// 注意矩阵要设置成我们推导结果的转置。
void BuildPerspectiveFovRHMatrix(Matrix4f& result, const float l, const float r, float b, float t, const float n, const float f)
{
    result.Set(0);

    result.m[0][0] = 2 * n / (r - l);
    result.m[1][1] = 2 * n / (t - b);
    result.m[2][0] = (r + l) / (r - l);
    result.m[2][1] = (t + b) / (t - b);
    if (g_DepthClipSpace == DepthClipSpace::kDepthClipZeroToOne)
    {
        result.m[2][2] = f / (n - f);
        result.m[3][2] = n * f / (n - f);
    }
    else /* g_DepthClipSpace == DepthClipSpace::kDepthClipNegativeOneToOne */
    {
        result.m[2][2] = (n + f) / (n - f);
        result.m[3][2] = (2 * n * f) / (n - f);
    }

    return;
}

(fov)式投影矩阵和(l,r,b,t)式投影矩阵的联系

这两个的关系非常明确，把我们推导fov矩阵时假设的参数代入就行了。l等于-1，r等于1，b等于-1/aspect，t等于1/aspect。代入之后，(l,r,b,t)式矩阵就变成

而这里的n是投影平面到原点的距离，也就是说

于是(l,r,b,t)式矩阵就和(fov)式矩阵画上等号了。如果n = 0.1，那么这个（l,r,b,t）式矩阵的xfov值就是168.58度。来看看运行效果：

OpenGL z范围[0, 1]

OpenGL z范围[-1, 1]

D3D12 z范围[0, 1]

D3D12 z范围[-1, 1]

OpenGL的显示还是比D3D12偏上一些，整个物体也变小很多，因为我们这次的xfov值太大了。

到这里，我们就可以回答本节最开始的问题了，对DX和OpenGL渲染管线来说，不存在裁剪空间[0,1]还是[-1,1]的区别，而之所以印象中有这区别，是因为在写DX和OpenGL代码时，所用的数学库一个是[0,1]，一个是[-1,1]。

如果相机空间是左手坐标系，那怎么办？

从最初的推理开始，左手坐标系改变了什么？投影平面的z坐标改变了，变成了随之而来的x和y坐标的表达式也变了

紧接着，我们不用再乘以-z，列出的矩阵也变了
$\begin{bmatrix}\cot({\frac{xfov}{2}}) && 0 && 0 && 0\\ 0 && aspect·(\cot{\frac{xfov}{2}}) && 0 && 0\\ 0 && 0 && m_3 && m_4\\ 0 && 0 && 1 && 0\end{bmatrix}·\begin{bmatrix}x \\ y \\ z \\ 1\end{bmatrix}=\begin{bmatrix} x·(\cot{\frac{xfov}{2}})\\ y·aspect·(\cot{\frac{xfov}{2}})\\ z·z'\\ z \end{bmatrix}$
求解m3和m4的方程也变了

n和f坐标地改变，导致代入方程的数据也变了，先计算z范围是[0,1]的转换矩阵

求得的结果是

最终转换矩阵为
$\begin{bmatrix}\cot({\frac{xfov}{2}}) && 0 && 0 && 0\\ 0 && aspect·(\cot{\frac{xfov}{2}}) && 0 && 0\\ 0 && 0 && -\frac{f}{n - f} && \frac{nf}{n - f}\\ 0 && 0 && 1 && 0\end{bmatrix}$
计算z范围是[-1,1]转换矩阵的方程是

解的m3和m4的值为

最终的投影矩阵是
$\begin{bmatrix}\cot({\frac{xfov}{2}}) && 0 && 0 && 0\\ 0 && aspect·(\cot{\frac{xfov}{2}}) && 0 && 0\\ 0 && 0 && -\frac{n+f}{n - f} && \frac{2nf}{n - f}\\ 0 && 0 && 1 && 0\end{bmatrix}$
编写代码实现这个投影矩阵

// 还是要注意我们要按照转置的思路去设置
void BuildPerspectiveFovLHMatrix(Matrix4f& result, const float xfov, const float aspect, const float near, const float far)
{
    result.Set(0);

    float cFov = 1.f / tanf(xfov / 2.f);
    result.m[0][0] = cFov;
    result.m[1][1] = aspect * cFov;
    result.m[2][3] = 1.0f;

    if (g_DepthClipSpace == DepthClipSpace::kDepthClipZeroToOne)
    {
        result.m[2][2] = -far / (near - far);
        result.m[3][2] = near * far / (near - far);
    }
    else
    {
        result.m[2][2] = -(far + near) / (near - far);
        result.m[3][2] = (2 * near * far) / (near - far);
    }

    return;
}

修改相应的代码查看效果

lefthand_OpenGL_zero_to_one

lefthand_OpenGL_negative_one_to_one

lefthand_D3D12_zero_to_one

lefthand_D3D12_negative_one_to_one

不用看盒子的显示状况，只需看显示的位置就可以了。因为这个场景是从blender导出的，而blender是右手坐标系的，所以它给出的顶点法线都是以右手坐标系给出的，我在这里做了一些小手脚，把摄像机放在了原点，在它背面放了一个盒子。用了一个左手坐标系的投影矩阵后，后面的盒子就显示出来了。可以看到，位置和右手坐标系及对应的OpenGL和D3D12图片是完全一致的，说明我们的推导没有问题。

那么，不用xfov的投影矩阵怎么办呢？

嗯，懒了，留给读者推导吧。

补充说明

本文用于测试的程序是我在github上的Panda项目。项目的使用方法是：
（1）首先你得有一个环境，Win10+VS2017+CMake+Git+Git-Lfs+github账号
（2）克隆项目到本地（克隆过程请耐心等待，原本github就不快，而且我项目里还有大文件，100M以上的那种），逐个运行build_assimp.bat，build_crossguid.bat，build_libpng.bat，build_opengex.bat，build_zlib.bat
（3）运行build.bat
（4）打开build文件夹下，Panda.sln解决方案。
（5）运行EditorD3D或是EditorOGL。
投影矩阵的生成函数在Numerical.cpp文件中，使用的地方在GraphicsManager.cpp的CalculateCameraMatrix()函数中。模型加载的地方是EditorLogic.cpp的Initialize()函数。上面用到的模型文件是article.dae和article_lefthand.dae，模型文件在根目录/Asset/Scene文件夹中，你可以随意尝试加载文件看效果。如果有什么困难，请在下方留言。

参考资料

《3D游戏与计算机图形学中的数学方法》
《Real-Time Render 4th Edition》
《3D Graphics for Game Programming》

【3D数学】——透视变换与相机偏手性