我昨天又忘了存啊啊啊啊啊啊啊啊啊啊啊啊啊
9.5
[国家集训队]数颜色
P1903 国家集训队]数颜色 bzoj2120
我TM!!!!又因为数组开小了调了两个小时!!!!!!
带修莫队 只是在普通莫队上加了一个时间 然后就和普通莫队操作差不多
bzoj上直接块大小为\(\sqrt{n}\)就能过 洛谷上加了这个块的的大小只能过6个点 ==吸氧过了
#include
using namespace std;
#define ll long long
#define Max(x,y) ((x)>(y)?(x):(y))
#define Min(x,y) ((x)<(y)?(x):(y))
#define Abs(x) ((x)<0?-(x):(x))
#define ls (o<<1)
#define rs (o<<1|1)
const int N=150000+5,M=1e6+5,inf=0x3f3f3f3f;
int n,m,block,a[N],b[N],cnt[M],ans[N];
template void rd(t &x){
x=0;int w=0;char ch=0;
while(!isdigit(ch)) w|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=w?-x:x;
}
int cq=0,cm=0;
struct quer{int l,r,tim,id;}q[N];
struct mdf{int pos,co,pre;}md[N];
bool cmp(quer A,quer B){
// return A.bl==B.bl?(A.r==B.r?A.timql) nw+=!cnt[a[--l]]++;
while(rqr) nw-=!(--cnt[a[r--]]);
while(timqt){
if(ql<=md[tim].pos&&md[tim].pos<=qr)
nw-=!(--cnt[a[md[tim].pos]])-!cnt[md[tim].co]++;
swap(a[md[tim].pos],md[tim].co),--tim;
}
ans[q[i].id]=nw;
}
for(int i=1;i<=cq;++i) printf("%d\n",ans[i]);
return 0;
} 主席树
又理解了一遍== 发现以前只是在背代码 压根不太理解
主席树的主要思想就是:保存每次插入操作时的历史版本,以便查询区间第k小
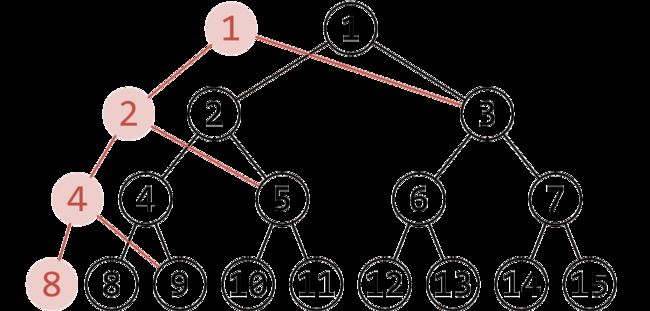
看图好理解嘿嘿嘿嘿 其实脑抽理解了好久....
只更改了 \(O(log\ n)\)个结点,形成一条链,也就是说每次更改的结点数 = 树的高度。
我们把问题简化一下:每次求 \([1,r]\)区间内的k小值。
怎么做呢?只需要找到插入 r 时的根节点版本,然后用普通权值线段树(有的叫键值线段树/值域线段树)做就行了。
那么这个相信大家很简单都能理解,把问题扩展到原问题——求\([l,r]\)区间k小值。
这里我们再联系另外一个知识理解: 前缀和 。
这个小东西巧妙运用了区间减法的性质,通过预处理从而达到 回答每个询问。
那么我们阔以发现,主席树统计的信息也满足这个性质。
所以……如果需要得到\([l,r]\)的统计信息,只需要用\([1,r]\)的信息减去\([1,l-1]\)的信息就行了。
那么至此,该问题解决!
#include
using namespace std;
#define ll long long
#define Max(x,y) ((x)>(y)?(x):(y))
#define Min(x,y) ((x)<(y)?(x):(y))
#define Abs(x) ((x)<0?-(x):(x))
const int N=2e5+5,M=100+5,inf=0x3f3f3f3f;
int n,m,a[N],w[N],tot=0,tl,rt[N];
template void rd(t &x){
x=0;int w=0;char ch=0;
while(!isdigit(ch)) w|=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=w?-x:x;
}
struct SegmentTree{int lc,rc,sum;}t[N*50];
void pup(int o){t[o].sum=t[t[o].lc].sum+t[t[o].rc].sum;}
void upd(int &o,int l,int r,int pre,int k){
o=++tot;
if(l==r){t[o].sum=t[pre].sum+1;return;}
int mid=l+r>>1;
if(k<=mid) upd(t[o].lc,l,mid,t[pre].lc,k),t[o].rc=t[pre].rc;
else upd(t[o].rc,mid+1,r,t[pre].rc,k),t[o].lc=t[pre].lc;
pup(o);
}
int query(int l,int r,int x,int y,int k){
if(l==r) return l;
int mid=l+r>>1,ss=t[t[y].lc].sum-t[t[x].lc].sum;
if(ss>=k) return query(l,mid,t[x].lc,t[y].lc,k);
else return query(mid+1,r,t[x].rc,t[y].rc,k-ss);
}
int main(){
// freopen("in.txt","r",stdin);
rd(n),rd(m);
for(int i=1;i<=n;++i) rd(a[i]),w[i]=a[i];
sort(a+1,a+n+1);
tl=unique(a+1,a+n+1)-a-1;
for(int i=1;i<=n;++i){
w[i]=lower_bound(a+1,a+tl+1,w[i])-a;
upd(rt[i],1,tl,rt[i-1],w[i]);
}
for(int i=1,l,r,k;i<=m;++i){
rd(l),rd(r),rd(k);
printf("%d\n",a[query(1,tl,rt[l-1],rt[r],k)]);
}
return 0;
} 试图学习带修主席树
宣布失败\(QAQ\)
高级数据结构杀我QAQ啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊
差分约束复习
1、\(a-b\geq c\;\ a−b≥c\),建边\(w[b,a]=c\)(表示a比b大c)
2、\(a−b≤c\)即\(b≥a−c\),建边\(w[a,b]=-c\)(表示b比a小c,注意不能建边\(w[b,a]=c\)因为这和第一个约束冲突,所以反过来就好了)
3、\(a==b\)时,建边\(w[a,b]=w[b,a]=0\)(表示a和b相等)
然后从0向i=1~n每个点连边\(w[0,i]=0\)(随便值为多少,反正只是验证可行性)
最后跑spfa求最长路,出现环则输出No,否则输出Yes
对于多个不等式组:
\(v(x1) - v(x2) >= c1\)
\(v(x2) - v(x3) >= c2\)
……
把它们加起来就会得到:\(v(x1) - v(xn) >= c1 + c2 + …… + cn-1\)
实际上上面的不等式组恰好可以看成一条路径,每个不等式即路径上的一小段。(路径总长等于每段路径长度之和)
单源最短路径问题中的三角形不等式。即对有向图中任意一条边