前言
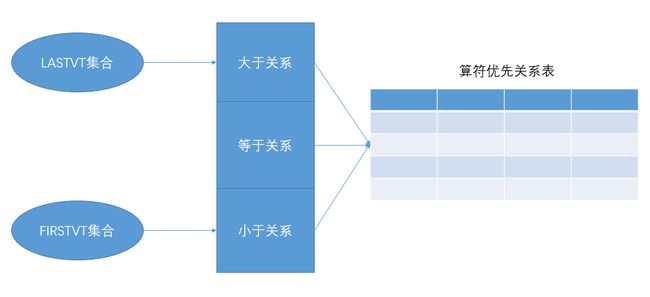
- 前面,我们已经知道了终结符之间的优先级关系是如何确定的,把确定的优先级关系以表格形式表现出来就有了算符优先关系表
两个集合
在前面对算符之间优先级关系的定义中,有一个现象是要去找一个非终结符的首终结符和尾终结符,为了便于计算机操作,定义如下两个概念
首终结符集:
FIRSTVT(B) = {b | B → b... 或 B → Cb... }尾终结符集:
LASTVT(B) = {b| B → ...b 或 B → ...bC}所以,对之前关于算符之间的优先级关系有了新的表示
1) = 关系: A → ...ab... 或 A → ...aBb...
2) < 关系: A → ...aB...,对于每一个 b ∈ FIRSTVT(B) , 都有a < b
3) > 关系: A → ...Bb...,对于每一个 a ∈ LASTVT(B),都有 a > b
FIRSTVT集合求解算法
两条规则
1)若存在产生式 A → a... 或 A → Ba...,则有 a ∈ FIRSTVT(A)
2)若存在 a ∈ FIRSTVT(B),且有产生式 A → B...,则有 a ∈ FIRSTVT(A)数据结构
1)一个布尔数组 F[m, n],【m:非终结符,n:终结符,为true时】,true表示该该终结符在该非终结符的FIRST集合中
2)一个栈,存放 (非终结符, 终结符) 二元组步骤
1)栈清空,不尔数组清空
2)按规则1,求到所有 FIRSTVT集合,并将二元组 (非终结符, 终结符) 入栈【非终结符:求FIRSTVT的非终结符元素,终结符:目前存在于该非终结符中的元素】
3)按规则2,弹出栈顶二元组(Q,a),查看所有的产生式,有无形如P → Q...,若有且a ∉ FIRSVT(P),则将布尔数组F[P,a]置为true,并将(P,a)入栈
4)重复步骤3,直至栈空最终,一行上的非终结符为true的都是该非终结符的FIRSTVT集合中的元素
LASTVT集合求解算法
两条规则
1)若存在产生式 A → ...a 或 A → ...aB,则有 a ∈ LASTVT(A)
2)若存在 a ∈ LASTVT(B),且有产生式 A → ...aB,则有 a ∈ FIRSTVT(A)数据结构
1)一个布尔数组 F[m, n],【m:非终结符,n:终结符,为true时】,true表示该该终结符在该非终结符的FIRST集合中
2)一个栈,存放 (非终结符, 终结符) 二元组步骤
1)栈清空,不尔数组清空
2)按规则1,求到所有 FIRSTVT集合,并将二元组 (非终结符, 终结符) 入栈【非终结符:求FIRSTVT的非终结符元素,终结符:目前存在于该非终结符中的元素】
3)按规则2,弹出栈顶二元组(Q,a),查看所有的产生式,有无形如P → ...Q,若有且a ∉ LASTVT(P),则将布尔数组F[P,a]置为true,并将(P,a)入栈
4)重复步骤3,直至栈空最终,一行上的非终结符为true的都是该非终结符的LASTVT集合中的元素
构造关系表算法
for(每条产生式 P → X1X2X3...Xn) {
for(i = 1;i <= n-1; ++i) {
if(X(i) 和 X(i+1) 均为终结符) {
X(i) = X(i+1)
}
if(i <= n-2 && X(i) 和X(i+2)均为终结符 && X(i+1) 为非终结符) {
X(i) = X(i+1)
}
if(X(i) 为终结符 && X(i+1)为非终结符) {
for(FIRSTVT(X(i+1))中的每一个元素a) {
Xi < a
}
}
if(X(i) 为非终结符 && X(i+1)为终结符) {
for(LASTVT(X(i))中的每一个元素a) {
a > X(i+1)
}
}
}
}
- 注
1)如果一个文法G按此算法构造出的优先表是没有重定义项的,文法G是算符优先文法
例子
- 构造下面文法的算符优先表
S → if Eb then E else E
E → E+T|T
T → T*F|F
F → i
Eb → b
解:
1)为了考虑语句的开始符号和结束符号"#",新增加一个产生式
S' → #S#
2)求解FIRST集合
1.规则1
FIRSTVT(S) = {if}
FIRSTVT(E) = {+}
FIRSTVT(T) = {*}
FIRSTVT(F) = {i}
FIRSTVT(Eb) = b
2.规则二
二元组:
(S,if), (E,+), (T, *), (F,i), (Eb,b)
--------------------------------------
栈:
栈:(S,if), (E,+), (T, *), (F,i), (Eb,b)
栈:(S,if), (E,+), (T, *), (F,i)
FIRSTVT(T) = {*} ∪ {i} = {*,i}
栈:(S,if), (E,+), (T, *),(T,i)
FIRSTVT(E) = {+} ∪ {i} = {+, i}
栈:(S,if), (E,+), (T, *),(E,i)
栈:(S,if), (E,+), (T, *)
FIRSTVT(E) = {+,i} ∪ {*} = {+, i,*}
栈:(S,if), (E,+),(E,*)
栈:(S,if), (E,+)
栈:(S,if)
栈:空
-----------------------------------------
∴ 最终
FIRSTVT(S) = {if}
FIRSTVT(E) = {+,i, *}
FIRSTVT(T) = {*,i}
FIRSTVT(F) = {i}
FIRSTVT(Eb) = b
2)求解LASTTV集合
1.规则一
LASTVT(S) = {else}
LASTVT(E) = {+}
LASTVT(T) = {*}
LASTVT(F) = {i}
LASTVT(Eb) = {b}
2.规则二
二元组:
(S,else), (E,+), (T,*), (F,i), (Eb,b)
栈:(S,else), (E,+), (T,*), (F,i), (Eb,b)
栈:(S,else), (E,+), (T,*), (F,i)
LASTVT(T) = {*} ∪ {i} = {*,i}
栈:(S,else), (E,+), (T,*), (T,i)
LASTVT(E) = {+} ∪ {i} = {+,i}
栈:(S,else), (E,+), (T,*), (E,i)
LASTVT(S) = {else} ∪ {i} = {else,i}
栈:(S,else), (E,+), (T,*), (S,i)
栈:(S,else), (E,+), (T,*)
LASTVT(E) = {+,i} ∪ {*} = {+,i,*}
栈:(S,else), (E,+), (E,*)
LASTVT(S) = {else,i} ∪ {*} = {else,i,*}
栈:(S,else), (E,+), (S,*)
栈:(S,else), (E,+)
LASTVT(S) = {else,i,*} ∪ {+} = {else,i,*,+}
栈:(S,else), (S,+)
栈:(S,else)
栈:空
∴最终
LASTVT(S) = {else,i,*,+}
LASTVT(E) = {+,i,*}
LASTVT(T) = {*,i}
LASTVT(F) = {i}
LASTVT(Eb) = {b}
3)优先关系表
1.等于关系
if = then
then = else
2.小于关系
if < FIRSTVT(Eb)
then < FIRSTVT(E)
else < FIRSTVT(E)
+ < FIRSTVT(T)
* < FIRSTVT(F)
# < FIRSTVT(S)
3.大于关系
LASTVT(Eb) > then
LASTVT(E) > else
LASTVT(E) > +
LASTVT(T) > *
LASTVT(S) > #
| if | then | else | + | * | i | b | # | |
|---|---|---|---|---|---|---|---|---|
| if | = | < | ||||||
| then | = | < | < | < | ||||
| else | < | < | < | > | ||||
| + | > | > | < | < | > | |||
| * | > | > | < | < | > | |||
| i | > | > | < | > | ||||
| b | > | |||||||
| # | < |
说明
- 求FIRSTVT和LASTVT的方法是计算机求的,人求的时候不用这么麻烦,比如 T → T * F | F ,求LASTVT(T) = { * } ∪ LASTTV( F ),一直递归下去就行
其它
课件下载:
关注下方微信公众号,
回复:
算符优先关系表的构造.code
欢迎加入交流群:451826376
更多信息:www.itcourse.top