Pyplot 模块
import matplotlib.pyplot as plt
- 确定坐标范围
- plt.axis([xmin,xmax,ymin,ymax])给定坐标范围
- xlim(xmin,xmax)和ylim(ymin,ymax)调整x,y的坐标范围
eg:
plt.axis([40, 160, 0, 0.03])
xlim(-2.5, 2.5)
#设置y轴范围
ylim(-1, 1)
-
图形对象
plt.figure()可以产生多个图,图片号按顺序增加,
注意:当前图和当前坐标,所有绘图操作仅对当前图和当前坐标有效。eg: plt.figure(1) 添加文字说明
- plt.text()可以在图中任意位置添加文字,支持LabTex语法
- xlable(),ylable()用于添加x轴和y轴标签
- title用于添加图的题目
eg:
plt.xlabel('Smarts')
plt.ylabel('Probability')
#添加标题
plt.title('Histogram of IQ')
#添加文字
plt.text(60, .025, r'$\mu=100,\ \sigma=15$')
- 文本注释
- plt.annotate():经常被用来注释图中的一些特征。
在使用中需要考虑来个点的坐标:被注释的地方xy(x,y)和插入文本的地方xytext(x,y)
eg:
plt.annotate('local max', xy=(2, 1), xytext=(3, 1.5),
arrowprops=dict(facecolor='black', shrink=0.05),
)
- 设置轴记号
plt.xticks()/plt.yticks():自定义坐标轴的刻度显示值
xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi], [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])
yticks([-1, 0, +1], [r'$-1$', r'$0$', r'$+1$'])
- 添加图例
plt.legend()
eg:
legend(loc='upper left')
- 分割图标
plt.subplot(2,3,1)表示把图标分割成2*3的网格。也可以简写plt.subplot(231)。其中,第一个参数是行数,第二个参数是列数,第三个参数表示图形的标号。
pyplot操作实例
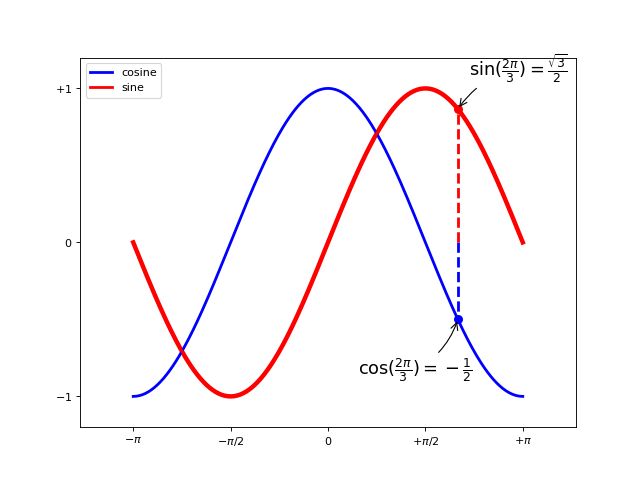
绘制正余弦函数图形并标注
code:
from pylab import *
#创建一个 8 * 6 点(point)的图,并设置分辨率为 80
figure(figsize=(8, 6), dpi=80)
# 创建一个新的 1 * 1 的子图,接下来的图样绘制在其中的第 1 块(也是唯一的一块)
subplot(1, 1, 1)
X = np.linspace(-np.pi, np.pi, 256, endpoint=True)
C, S = np.cos(X), np.sin(X)
# 绘制余弦曲线,使用蓝色的、连续的、宽度为 1 (像素)的线条
plot(X, C, color="blue", linewidth=1.0, linestyle="-")
# 绘制正弦曲线,使用绿色的、连续的、宽度为 1 (像素)的线条
plot(X, S, color="r", lw=4.0, linestyle="-")
plt.axis([-4, 4, -1.2, 1.2])
# 设置轴记号
xticks([-np.pi, -np.pi / 2, 0, np.pi / 2, np.pi],
[r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])
yticks([-1, 0, +1],[r'$-1$', r'$0$', r'$+1$'])
# 在屏幕上显示
plot(X, C, color="blue", linewidth=2.5, linestyle="-", label="cosine")
plot(X, S, color="red", linewidth=2.5, linestyle="-", label="sine")
plt.legend(loc='upper left')
t = 2 * np.pi / 3
# 作一条垂直于x轴的线段,由数学知识可知,横坐标一致的两个点就在垂直于坐标轴的直线上了。这两个点是起始点。
plot([t, t], [0, np.cos(t)], color='blue', linewidth=2.5, linestyle="--")
scatter([t, ], [np.cos(t), ], 50, color='blue')
plt.annotate(r'$\sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$',
xy=(t, np.sin(t)), xycoords='data',
xytext=(+10, +30), textcoords='offset points', fontsize=16,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plot([t, t], [0, np.sin(t)], color='red', linewidth=2.5, linestyle="--")
scatter([t, ], [np.sin(t), ], 50, color='red')
annotate(r'$\cos(\frac{2\pi}{3})=-\frac{1}{2}$',
xy=(t, np.cos(t)), xycoords='data',
xytext=(-90, -50), textcoords='offset points', fontsize=16,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
show()