二叉树的遍历 递归 非递归 Java

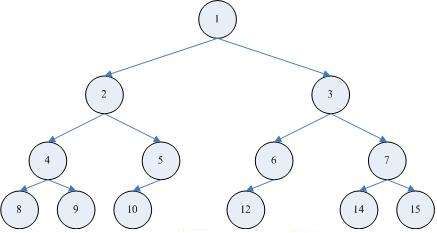
二叉树的常用遍历算法实现

二叉树的形状.png

首先定义 二叉树，节点值，左子节点，右子节点

public class TreeNode {
    private int value;
    private TreeNode left;
    private TreeNode right;
    public TreeNode(int value) {
        this.value = value;
    }
}

前序遍历

• 递归实现

public static void preOrder(TreeNode treeNode) {
    if (treeNode != null) {
        System.out.print(treeNode.value + " ");
        preOrder(treeNode.left);
        preOrder(treeNode.right);
    }
}

• 非递归实现（1）
  • 这个是常规思路，先遍历到根节点，并打印、压栈，然后遍历其左子节点，打印、压栈。
  • 若左子节点已经是叶子节点，则 while 循环结束，开始从栈中弹出根节点，并访问根节点的右子树，直到栈为空，则遍历结束。

public static void preOrderStack(TreeNode treeNode) {

    if (treeNode == null) {
        return;
    }
    Stack stack = new Stack();
    TreeNode root = treeNode;
    
    while (root != null || !stack.isEmpty()) {
        while (root != null) {
            //  注意和 中序非递归的区别，这里是先打印节点值，再去加入栈中
            System.out.print(root.value + " ");
            stack.push(root);
            root = root.left;
        }
        if (!stack.isEmpty()) {
            root = stack.pop();
            root = root.right;
        }
    }
}

• 非递归实现（2）
  • 这里的思路是利用栈先进后出的性质， 先将根节点入栈
  • 循环中，弹出根节点，然后先加入右子节点，后加入左子节点
  • 再一次循环，新弹出的节点就是刚压入的左子节点

public static void preOrderStack1(TreeNode treeNode) {
    if (treeNode == null) {
        return;
    }
    Stack stack = new Stack();
    stack.push(treeNode);
    while (!stack.isEmpty()) {
        TreeNode root = stack.pop();
        System.out.print(root.value + " ");
        if (root.right != null) {
            stack.push(root.right);
        }
        if (root.left != null) {
            stack.push(root.left);
        }
    }
}

中序遍历

• 递归实现

public static void midOrder(TreeNode treeNode) {
    if (treeNode != null) {
        midOrder(treeNode.left);
        System.out.print(treeNode.value + " ");
        midOrder(treeNode.right);
    }
}

• 非递归实现
  • 中序遍历是 左 根 右

public static void midOrderStack(TreeNode treeNode) {
    if (treeNode == null) {
        return;
    }
    Stack stack = new Stack();
    while (treeNode != null || !stack.isEmpty()) {
        while (treeNode != null) {
            stack.push(treeNode);
            treeNode = treeNode.left;
        }
        if (!stack.isEmpty()) {
            treeNode = stack.pop();
            System.out.print(treeNode.value + " ");
            treeNode = treeNode.right;
        }
    }
}

后序遍历

• 递归实现

public static void postOrder(TreeNode treeNode) {
    if (treeNode != null) {
        postOrder(treeNode.left);
        postOrder(treeNode.right);
        System.out.print(treeNode.value + " ");
    }
}

• 非递归实现
  • 由于后序遍历二叉树的顺序是 左 右 根，故可以使用中间临时栈保存 根 右 左 的遍历结果

public static void postOrderStack(TreeNode treeNode) {
    Stack stack = new Stack();
    Stack stack1 = new Stack();
    while (treeNode != null || !stack.isEmpty()) {
        while (treeNode != null) {
            stack.push(treeNode);
            stack1.push(treeNode);
            treeNode = treeNode.right;
        }
        if (!stack.isEmpty()) {
            treeNode = stack.pop();
            treeNode = treeNode.left;
        }
    }
    while (!stack1.isEmpty()) {
        TreeNode treeNode1 = stack1.pop();
        System.out.print(treeNode1.value + " ");
    }
}

层次遍历

public static void levelOrder(TreeNode treeNode) {
    if (treeNode == null) {
        return;
    }
    Queue queue = new LinkedList<>();
    queue.add(treeNode);
    while (!queue.isEmpty()) {
        TreeNode root = queue.poll();
        System.out.print(root.value + " ");

        if (root.left != null) {
            queue.add(root.left);
        }
        if (root.right != null) {
            queue.add(root.right);
        }
    }
}

“之” 字型遍历

public static void printZ(TreeNode treeNode){
    if (treeNode == null){
        return;
    }
    Stack stack1 = new Stack<>();
    Stack stack2 = new Stack<>();
    stack1.push(treeNode);
    boolean flag = true;
    while (!stack1.isEmpty() || !stack2.isEmpty()){
        if (flag){
            while (!stack1.isEmpty()) {
                treeNode = stack1.pop();
                System.out.print(treeNode.value+" ");
                if (treeNode.left != null) {
                    stack2.add(treeNode.left);
                }
                if (treeNode.right != null) {
                    stack2.add(treeNode.right);
                }
            }
        }else {
            while (!stack2.isEmpty()) {
                treeNode = stack2.pop();
                System.out.print(treeNode.value+" ");
                if (treeNode.right != null) {
                    stack1.add(treeNode.right);
                }
                if (treeNode.left != null) {
                    stack1.add(treeNode.left);
                }
            }
        }
        flag = flag ^ true;
    }
}

求最大深度

• 递归实现

public static int getDepth(TreeNode treeNode) {
    if (treeNode == null) {
        return 0;
    }
    int left = getDepth(treeNode.left);
    int right = getDepth(treeNode.right);
    return left > right ? left + 1 : right + 1;
}

• 非递归实现

public static void getDepth1(TreeNode treeNode){
    if (treeNode == null){
        return;
    }
    Queue queue = new LinkedList<>();
    queue.add(treeNode);
    int depth = 0;
    while (!queue.isEmpty()){
        int size = queue.size();
        while (size > 0){
            treeNode = queue.poll();
            if (treeNode.left != null){
                queue.add(treeNode.left);
            }
            if (treeNode.right != null){
                queue.add(treeNode.right);
            }
            size--;
        }
        depth++;
    }
    System.out.println(depth);
}

求最大宽度

• 对于二叉树，每一层的节点数是不一样的，计算二叉树中具有结点数最多的那一层的结点个数
  用队列实现，实质就是当当前层节点弹出，加入下一层节点

public static void getWidth(TreeNode treeNode) {
    // 根节点为空，则 最大宽度为 0 ；
    if (treeNode == null) {
        return;
    }
    // 此时根节点入队，最大宽度为 1 
    int max = 1;
    Queue queue = new LinkedList<>();
    queue.add(treeNode);

    // 注意循环条件：队列不为空
    while (!queue.isEmpty()) {
        // 记录当前层的节点数
        int size = queue.size();  

        // 把当前层的所有节点依次弹出，循环结束时，当前层节点会全部弹出，此时队列中只包含下一层的所有节点
        while (size > 0) {   

            treeNode = queue.poll();
            size--;

            // 弹出的同时把下一层的节点加入队列中
            if (treeNode.left != null) {
                queue.add(treeNode.left);   
            }
            if (treeNode.right != null) {
                queue.add(treeNode.right);
            }
        }
       // 此时队列中存放的是下一层的所有节点，比较它与上一层节点的个数，保存较大值
        if (max < queue.size()) {
            max = queue.size();
        }
    }
    System.out.println(max);
}

用数组列表实现求最大宽度，类比队列，用两个指针 i，j。i 指向当前层节点第一个，j 指向当前层最后一个。弹出时 i++ ，加入元素时 j++；

public static void levelOrder(TreeNode treeNode){
    if (treeNode == null){
        return;
    }
    List list = new ArrayList();
    list.add(treeNode);
    int max = 1;
    int i =0;
    int j = 0;
    // i，j 最多相等，遍历到最后一个元素时，i = j ，此时 i 节点左右子节点为空，下一步 i 将 大于 j ，循环结束
    while (i <= j){
        // 临时保存当前层的节点数
        int size = j-i+1;
        while (size > 0){
            treeNode = list.get(i);
            if (treeNode.left != null){
                list.add(treeNode.left);
                j++;
            }
            if (treeNode.right != null){
                list.add(treeNode.right);
                j++;
            }
            size--;
            i++;
        }
        if (max < j-i+1){
            max = j-i+1;
        }
    }
    System.out.println(max);
}