结对编程(python实现)

一、Github项目地址：https://github.com/asswecanfat/git_place/tree/master/oper_make

二、PSP2.1表格:

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	150	150
· Estimate	· 估计这个任务需要多少时间	150	150
Development	开发	1340	1720
· Analysis	· 需求分析	50	60
· Design Spec	· 生成设计文档	40	60
· Design Review	· 设计复审	30	30
· Coding Standard	· 代码规范	20	20
· Design	· 具体设计	100	120
· Coding	· 具体编码	1000	1250
· Code Review	· 代码复审	60	80
· Test	· 测试（自我测试，修改代码，提交修改）	40	100
Reporting	报告	90	130
· Test Report	· 测试报告	50	80
· Size Measurement	· 计算工作量	20	20
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	20	30
合计		1580	2000

 

---

三、效能分析

1.使用了自己写的上下文管理器来记录时间和比较性能（因为click模块的原因导致内置的timeit模块不太好用）

2. 优化过程：

a.在之前的write_file文件中，里面的write_in_file方法是每调用一次就打开一次文件，生成一万道题要16.3秒（忘记截图了）

b.通过将math_op中的迭代器和字典--列表结构当做参数传进去，在write_in_file方法里进行迭代，时间变为2~3秒

 

 

 

 

---

四、设计实现过程

　　1.在看了题目后，我们两个人就在晚上进行了讨论，先是对数学表达式的查重的数据结构进行了探索，一开始想用字典，O(1)的查询时间，但由于键值可能重复就放弃了，最后我想到了用+-*/列表链接子在一起的方法，但在实现的过程中，我们还是改成了构建统一的二叉树，以便于查重。在生成数学表达式中，我用了分层递归，就是一个函数，随机选取层数，最大为3，最小为1，进行n=层数的2次递归，实现了完全随机的数学表达式。

　　2.思路是先接收-n和-r参数来控制运算式的数量和数值的范围，通过层数递归和随机数类（该类可以生成分数（无论真假）和整数）和括号随机生成方法生成数学表达式字符串，难点是如何构造统一二叉树。

　　3.数学表达式字符串我们使用了逆波兰表达式，也就是后缀表达式，将数学表达式传递给AnalyOp.check_math_opj静态方法进行处理，决定是否报错还是返回子式列表，逆波兰表达式和答案。我们借鉴了网上的源码，后来发现里面的源码有缺陷，自己动手修改了源码，解决了没有括号时产生的BUG，生成了有优先级的，只有两个数进行运算的子式列表和逆波兰表达式，还有答案。

　　4.然后将子式列表和逆波兰表达式传递给查重的模块并决定写入，难点在于如何构建统一的二叉树，后面我使用了一个标识符——最小位解决了该问题，并构建了字典--列表的数据结构进行O(1+m)的查询，其中键为答案，同一个答案先比较列表中的二叉树是否一样再决定插入。

　　5.由于click的特殊性，其中-n或-r后必须都加参数。

　　6.用Fraction类来构建整数和分数，该类很好的实现了__add__()等两数之间的运算的魔法方法

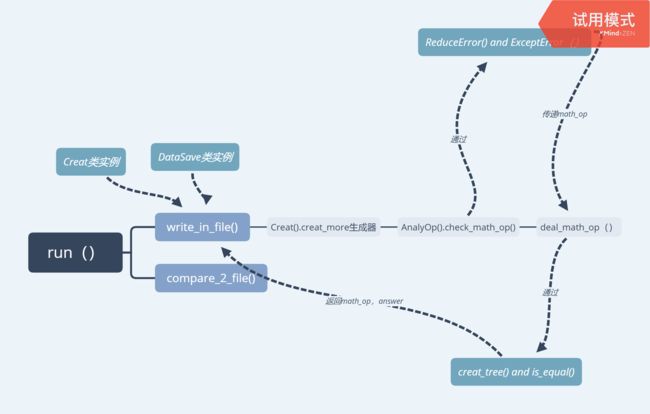
代码结构功能说明：

data_sturct.py：定义了字典--列表和树节点的数据结构（DataSave类和Node类）

duplicate_check.py：定义了二叉树的构建和查重（creat_tree方法和is_equal方法）

main.py：用于运行的run方法

math_op.py：定义了Creat类，里面有构建单个数学表达式的creator方法和构建多个的creat_more的生成器

math_op_analysis.py:定义了AnalyOp类，使用栈实现逆波兰和计算， 还有静态方法check_math_op检查math_op合法性

num_creat.py：定义了NumCreat类，随机生成分数（无论真分数假分数），还有假分数转真分数的静态方法

op_error.py：继承父类ValueError， 子类ReduceError和ExceptError

wirte_file.py：定义了处理数学表达式math_op， answer含有的假分数，写入文件的方法

 

 

 

 

 

 

---

五、 代码说明

1.创造数学表达式类

class Creat(object):
    def __init__(self, max_num: int, formula_num: int):
        self.max_num = max_num  # 最大范围
        self.formula_num = formula_num  # 公式最大条数
        self.level = random.randint(2, 4)  # 递归层数
        self.start_level = 0  # 递归开始层
        self.first_level = random.randint(1, self.level - 1)  # 第一个子式递归次数
        self.second_level = self.level - self.first_level  # 第二个子式递归次数
        self.operator = {
            1: '+',
            2: '-',
            3: '*',
            4: '÷',
        }

    def creator(self) -> str:
        math_op = '{}{}{}{}{}'.format(
            self.__creat_math_op(self.first_level),  # 第一个子式
            ' ',
            self.operator[random.randint(1, 4)],  # 随机选取运算符
            ' ',
            self.__creat_math_op(self.second_level),  # 第二个子式
        )
        return math_op

    def __creat_math_op(self, level_choice: int) -> str:
        random_num = random.randint(0, 1)
        self.start_level += 1
        if self.start_level == level_choice:
            self.start_level = 0
            return random.randint(0, self.max_num)
        math_op = '{}{}{}{}{}{}{}'.format(
            self.__brackets(random_num, 0),  # '('
            NumCreat(self.max_num).choices_num(),  # 随机数
            ' ',
            self.operator[random.randint(1, 4)],  # 随机选取运算符
            ' ',
            self.__creat_math_op(level_choice),  # 'xx +|-|*|/ xx'
            self.__brackets(random_num, 1),  # ')'
        )
        self.start_level = 0
        return math_op

    def __brackets(self, random_num: int, choice: int) -> str:  # 决定括号是否填入
        if random_num:
            if choice:
                return ')'
            else:
                return '('
        return ''

    def creat_more(self, data_save):  # 迭代器
        op_num = 0
        while op_num < self.formula_num:
            math_op = self.creator()
            try:
                postfix, answer = AnalyOp.check_math_op(math_op)
                math_op = deal_math_op(math_op, list(postfix), answer, data_save)
                if math_op:
                    yield (math_op, answer)
                    op_num += 1
            except (ExceptError, ReduceError, ZeroDivisionError):
                pass
            self.__init_variable()

    def __init_variable(self):  # 初始化以下值
        self.start_level = 0
        self.level = random.randint(2, 4)
        self.first_level = random.randint(1, self.level - 1)
        self.second_level = self.level - self.first_level

2.构建逆波兰表达式

class AnalyOp(object):  # 使用逆波兰表达式解析
    OPERATOR = ('+', '-', '*', '÷', '(', ')')  # 运算符常量

    def __init__(self, math_op):
        self.math_op = math_op.replace('(', '( ').replace(')', ' )')
        self.math_op = self.math_op.split()
        self.postfix_deque = deque()  # 后缀表达式栈
        self.operators_deque = deque()  # 运算符栈
        self.operators_priority = {  # 运算符优先级
            '+': 1,
            '-': 1,
            '*': 2,
            '÷': 2,
        }

    def __clear_deque(self):  # 用于清空栈
        self.postfix_deque.clear()
        self.operators_deque.clear()

    def mathop_to_postfix(self):
        """将中缀表达式转换为后缀表达式。"""
        for i in self.math_op:
            if self.is_num(i):
                self.postfix_deque.append(i)
            elif i in self.OPERATOR:
                if i == '(':
                    self.operators_deque.append(i)
                elif i == ')':
                    self.__pop_to_left_bracket()
                else:
                    self.__compare_and_pop(i)
        self.__pop_rest()
        return self.postfix_deque

    @staticmethod
    def is_num(text):  # 判断是否为数字
        if '/' in text:
            return True
        return text.isdigit()

    def __pop_to_left_bracket(self):
        """依次弹栈并追加到后缀表达式，直到遇到左括号为止。"""
        while self.operators_deque:
            operator = self.operators_deque.pop()
            if operator == '(':
                break
            self.postfix_deque.append(operator)

    def __compare_and_pop(self, text):
        """比较优先级并进行相应操作。"""
        if not self.operators_deque:
            self.operators_deque.append(text)
            return
        while self.operators_deque:
            operator = self.operators_deque.pop()
            if operator == '(':
                self.operators_deque.append('(')
                self.operators_deque.append(text)
                return
            elif self.operators_priority[text] > self.operators_priority[operator]:
                self.operators_deque.append(operator)
                self.operators_deque.append(text)
                return
            elif text == operator:
                self.postfix_deque.append(operator)
            else:
                self.postfix_deque.append(operator)
        self.operators_deque.append(text)

    def __pop_rest(self):
        """弹出所有剩余的运算符，追加到后缀表达式。"""
        while self.operators_deque:
            self.postfix_deque.append(self.operators_deque.pop())

    def parse_out_son(self):
        """只解析出有优先级的子式"""
        postfix = deepcopy(self.mathop_to_postfix())
        num_deque = deque()
        son_op_list = []
        answer = None
        for i in self.postfix_deque:
            if self.is_num(i):
                num_deque.append(i)
            else:
                right_num = num_deque.pop()
                left_num = num_deque.pop()
                son_op = f'{left_num}{i}{right_num}'
                son_op_list.append(son_op)
                answer = self.operation_func(i)(left_num, right_num)
                num_deque.append(answer)
        self.__clear_deque()
        return son_op_list, postfix, str(answer)

    @staticmethod
    def operation_func(operator):  # 选择运算方法
        operation_dict = {
            '+': lambda x, y: Fraction(x) + Fraction(y),
            '-': lambda x, y: Fraction(x) - Fraction(y),
            '*': lambda x, y: Fraction(x) * Fraction(y),
            '÷': lambda x, y: Fraction(x) / Fraction(y),
        }
        return operation_dict[operator]

3.统一二叉树构建

def creat_tree(postfix_deque):  # 创建统一的二叉树
    """_min为树结点的最小标志位，左子树小，右子树大"""
    node = deque()
    for i in postfix_deque:
        if AnalyOp.is_num(i):
            node.append(Node(num=i, answer=i, _min=i))
        else:
            max_num, min_num = node.pop(), node.pop()
            if i != '÷' and i != '-':
                if max_num.answer == min_num.answer:
                    max_num, min_num = (max_num, min_num) \
                        if Fraction(max_num._min) >= Fraction(min_num._min) \
                        else (min_num, max_num)
                else:
                    max_num, min_num = (max_num, min_num) \
                        if Fraction(max_num.answer) > Fraction(min_num.answer) \
                        else (min_num, max_num)
            op = Node(operator=i,
                      right_child=max_num,
                      left_child=min_num,
                      answer=AnalyOp.operation_func(i)(min_num.answer, max_num.answer),
                      _min=min_num._min,)
            node.append(op)
    return node.pop()

4.题目/答案文件生成

def write_in_file(creat, data_save):  # 写入文件
    with open(r'./Exercises.txt', 'a', encoding='utf-8') as q:
        with open(r'./Answers.txt', 'a', encoding='utf-8') as a:
            for num, (math_op, answer) in enumerate(creat.creat_more(data_save)):
                answer = deal_answer(answer)
                q.write('{}.{} = {}'.format(num + 1,
                                            math_op,
                                            '\n', ))
                a.write('{}.{}{}'.format(num + 1,
                                         answer,
                                         '\n'))
                print('{}{}{}'.format('\r', num + 1, '条题目已生成！！'), sep='', end='', flush=True)

5.文件之间的比较

def compare_2_file(f1, f2):  # f1是题目文件，f2是答案文件
    coding1 = _get_coding(f1)
    coding2 = _get_coding(f2)
    if coding1 is not None and coding2 is not None:
        with open(f1, 'r', encoding=coding1) as f1:
            with open(f2, 'r', encoding=coding2) as f2:
                with open(r'.\Grade.txt', 'w', encoding='utf-8') as g:
                    right_num = 0
                    right_answer = []
                    wrong_num = 0
                    wrong_answer = []
                    f1_dict = _deal_lsit(f1)
                    f2_dict = _deal_lsit(f2)
                    for i in f1_dict.keys():
                        if f1_dict[i] == f2_dict[i]:
                            right_num += 1
                            right_answer.append(i)
                        else:
                            if f1_dict[i] != '':
                                wrong_num += 1
                                wrong_answer.append(i)
                    g.write(f'Correct: {right_num} ({right_answer[0]}')
                    for i in right_answer[1:]:
                        g.write(f', {i}')
                    g.write('){}Wrong: {} ({}'.format('\n', wrong_num, wrong_answer[0]))
                    for i in wrong_answer[1:]:
                        g.write(f', {i}')
                    g.write('){}'.format('\n'))


def _deal_lsit(f) -> dict:
    f_list = list(map(lambda x: re.split(r'\.(.+= ?)?', x), f.readlines()))  # 用于分开题目序号和答案
    return {i[0]: i[2].rstrip('\n') for i in f_list}


def _get_coding(f):  # 处理文件的编码，以防报错
    text = open(f, 'rb').read()
    return chardet.detect(text)['encoding']

 

---

 

六、测试运行 

 1. 测试-n -r 功能：

　　　　a. 单道题目生成和结果正确

　　　　

 

 　　　b. 两道题目生成和结果正确，-n参数处理正确(与a比较)

　　

 

 　　c.-r为负数

 

　　d.-n为负数

　　e.只有-r

 

　　f.只有-n

　　

　　g.测试生成10000道题

　　

 

 

 

 

2 测试验证功能-e -a

　　　　a 测试正确的答案文件

　　　　

 

 　　

 

 

 

 　　b.测试-e和-a指令

 

 

 

　　c.只有一个指令

 

 

 

 

 3.由于我是递归生成的数学表达式，最多递归4层（总和），不会出现4个以上及4个的运算符

 

 

---

 

七、项目小结 

　　1.本次项目使用python实现，使用了click处理命令行参数，将中缀表达式转化为后缀表达式以实现数学表达式的解析，使用递归生成子式的方式生成题目，题目中的数字可以为整数或真分数、在生成题目时同步生成答案；在判断提交答案正确率时用正则获取提交部分并将其与正确答案进行比对。

　　2.第一次接触结对编程这种开发模式，深刻的感受到讨论与监督对于编程任务实现的推进作用，两个人的思路碰撞之后可以推进出更新更全面的想法与思路。