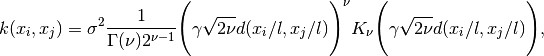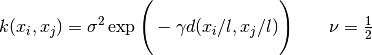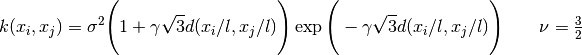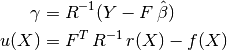原文章为scikit-learn中"用户指南"-->"监督学习的第七节:Gaussian Processes"######
高斯过程(GP)是一种被设计来解决** 回归 和 概率分类 **的通用监督学习方法。
高斯过程有以下的优点:
- 可以预测插值(至少对常规核而言)
- 预测是概率的(高斯分布的)结果,因此可以根据置信区间的计算以决定是否要在一些感兴趣的区域重新进行拟合(在线拟合,自适应拟合)。
- 可以指定不同的 核 。默认是提供了一个普通核,不过也可以根据自己需求来指定自定义的核。
同样的,其缺点有:
- 它是非稀疏的。即它会使用所有样本及其特征信息来进行预测。
- 在高维空间下会失去效率(当特征数量超过3、40左右)。
1.7.1. 高斯过程回归(GPR)#
GaussianProcessRegressor 类实现了高斯过程的回归。所以要使用它前需要指定先验。先验均值被预设值为全为0的常数(当** normalize=False 时)或是训练集的均值(当 normalize=True )。先验的协方差是通过核对象来指定的。而核的超参数则是在拟合通过最大对数边际似然(LML)的GPR过程中,通过传入 optimizer 来进行调优。因为LML可能拥有多个局部最优值,所以可以通过设置 n_restarts_optimizer 来反复进行此过程以获得"最优值"。这个过程的第一次运行通常是先初始化核的超参数。然后再从可能的值域中随机的对超参数赋值。如果要让初始化的超参数保持不变,那么只需要传入 None **作为它的优化器就可以了。
可以通过参数** alpha **指定Target(目标结果)的噪声等级,可以当做一个全局标量 或 每个数据点的噪声等级。因为设置一个中等的噪声等级会被以Tikhonov正则化形式来实现,这一点有助于解决在拟合过程中出现的数值问题(即把它添加到核矩阵的对角线内)。另一种明确指定噪声等级的可选的方法是:在核中包含一个白核组件,这样就可以在数据集中估计出全局噪声等级(可以看下面的例子)。
本类的实现是基于[RW2006]的 2.1 算法。除了scikit-learn提供的标准API方法外,高斯过程回归(GPR):
- 允许在没有先验的情况下进行拟合(基于GP先验)。
- 提供一个额外的方法** sample_y(X) **,这个方法可以评估从GPR(之前或之后)提取的样本。
- 提供** log_marginal_likelihood(theta) **方法,其可以作为一种在外部选择超参数的方法,例如通过马尔科夫链蒙特卡洛算法(MCMC)。
1.7.2. GPR的一些例子#
1.7.2.1. 能估计噪声等级的GPR
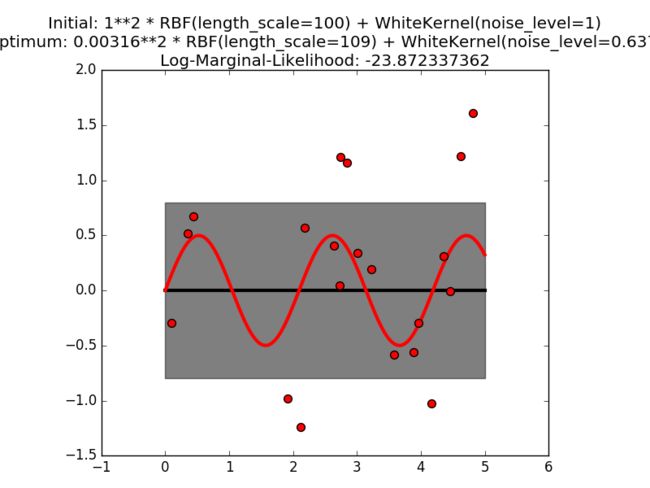
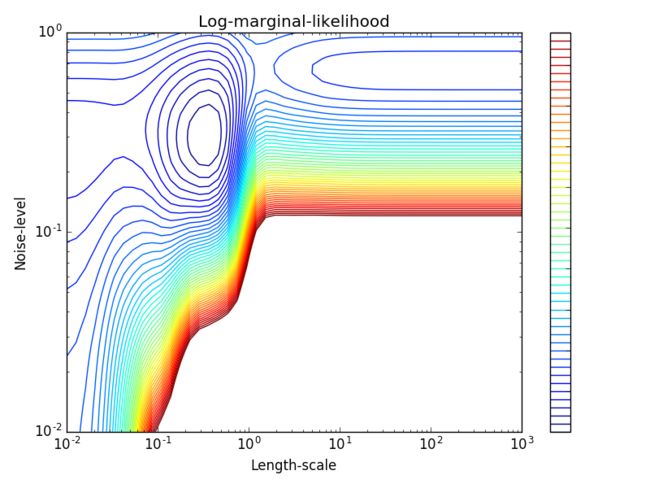
这个例子展示了带有 WhiteKernel 的sum核GPR能够估量数据的噪声等级。下面LML的绘图显示了其存在有两个局部最大值。
这一张图代表了一个带有高度噪声等级和大长度标量的模型,其解释了噪声对数据的影响程度。
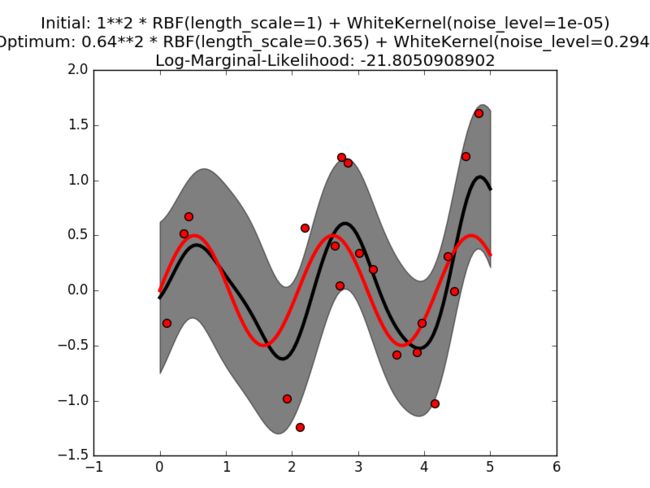
第二张图的模型有着一个较小的噪声等级和小长度标量,展示了无噪声函数的变化关系。这一张图有着对数据集的高度似然性;但是根据超参数的初始化值来看,在使用基于梯度的优化方法可能会生成一个具有高噪声的结果。正因为要避免出现这种情况,所以才要使用多种不同的超参数初始化值来重新训练。
1.7.2.2. GPR与核岭回归的比较##
核岭回归(KRR)和GPR都是使用了内置的"核技巧"来学习目标函数。KRR通过由各种核在原始空间里对应的非线性函数所形成的空间里来学习线性函数。这个在核空间内的线性函数是由基于带有均方误差损失的岭回归来得出的。GPR使用核来定义一个在目标函数上先验分布的协方差并使用经过训练的数据来定义似然函数。基于贝叶斯理论,定义了一个在目标函数上的(高斯)后验分布,并且使用它的平均值来作为预测结果。
GPR与KRR的一个主要的不同点在于,GPR能够使用基于梯度上升的边际似然函数来选择核所需的超参数,而KRR则需要对交叉验证的损失函数(均分误差损失函数)执行网格搜索才可以得出超参数。另一个区别点在于GPR是学习目标函数的生成性概率模型,
从而能为预测结果提供有意义的置信区间和后验样本;而KRR只能提供一个预测结果。
下面的图表比较了这两种方法在一个由带有强噪声正弦波分布的人工数据集上的学习结果。KRR和GPR的模型都是基于正弦平方核学习出的,这种核很适合用来学习具有周期性规律分布的数据。正弦平方核的超参数控制着平滑度(也就是长度标量)和核的周期性。除此之外,当前数据集的噪声等级还是通过添加额外的白核组件的GPR和经过正则化参数** α **的KRR得出的。
这个图表展示了两个方法各自对目标函数的合理模型。GPR得出的模型正确地得出这个周期函数大致为** 2 * π (6.28),而KRR则得出了双倍的结果 4 * π 。除此之外,GPR为预测值提供了一个合理的置信区间,虽然这个区间不能用到KKR上。这两个方法的另一种主要区别是预测和拟合的时间:理论上KRR的拟合速度是很快的,因为为超参数调优的网格搜索速度与超参数的数量成正比(不过同样也会受到维度灾难**的影响)。GPR中优化参数所使用的基于梯度的优化方法并不会受到指数缩放的影响,而在这里例子中,因为超参数的空间是三维的,所以处理的速度非常快。然后预测所需的时间也是类似的,但是如果要使GPR产生预测分布的方差的话,其所需的时间要比只预测出平均值要更久。
1.7.2.3. GPR与莫纳罗亚山的二氧化碳数据##
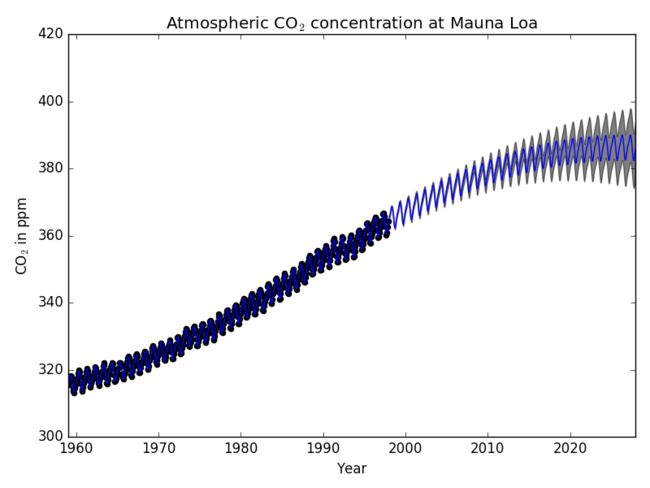
这个例子是基于[RW2006]的5.4.3一节。它描绘了一个使用了复杂内核工程和使用梯度上升为对数边际似然优化超参数。这个数据集由1958年至1997年,夏威夷的莫纳罗亚山上每月平均大气CO2浓度(百万分之一(ppmv))的观察数据组成。训练出的模型目标是为了获取CO2浓度跟时间** t **的关系函数。
这个核由一些术语组成,这些术语负责解释信号的不同属性:
- 一个长期且平滑上升的趋势将由RBF核来进行解释。拥有大长度标量的RBF核会强制该组件变得平滑。而上升的趋势则是留给GP自由选择是否强制需要。特定长度标量和振幅属于该核的自由超参数。
- 季节性的则由一个周期性的正弦平方核进行解释,周期为一年。长度标量也是一个周期性组件,控制着模型的平滑度,这是一项自由参数。为了允许远离精确周期性,采用具有RBF内核的乘积。这个RBF核内的长度标量控制着远离时间,并且它也是一个自由参数。
- 较小的不规则中期则由有理数核组件(拥有长度标量和alpha两个参数,后者决定长度标量的扩散性)来进行解释。根据[RW2006],这些不规则的项用有理数核来解释比RBF核组件更好,因为前者可以容纳几个长度标量。
- 由RBF核贡献的"噪声"项,则是应该解释相关的噪声分量,例如局部天气现象和白核对白噪声的贡献。它的相对幅度和RBF的长度标量也是自由参数。
在减去目标的平均值之后,最大化对数边际似然函数使得产生出一个带有LML为-83.214的核:
34.4**2 * RBF(length_scale=41.8)
+ 3.27**2 * RBF(length_scale=180) * ExpSineSquared(length_scale=1.44,
periodicity=1)
+ 0.446**2 * RationalQuadratic(alpha=17.7, length_scale=0.957)
+ 0.197**2 * RBF(length_scale=0.138) + WhiteKernel(noise_level=0.0336)
因此大部分目标信号(34.4ppm)的趋势可以通过成一个长期上升的趋势(长度标量为41.8年)进行解释。这个周期组件拥有一个3.27ppm的振幅,衰退时间为180年且长度标量为1.44。较长的衰退时间表示我们拥有一个局部非常接近周期性季节的组件。相关的噪声拥有为0.197ppm的振幅,长度标量为0.138年,而白噪音贡献为0.197ppm。因此全局 噪声水平很低,代表着数据能够很好地通过模型来解释。下面的图表还展示了该模型在2015年左右所做出的一个非常有信心的预测。
1.7.3. 高斯处理分类(GPC)#
GaussianProcessClassifier
实现了用于分类的高斯过程(GP),更具体来说是用在概率分类,使用类概率的形式来作为预测结果。GPC在潜在函数** f 上使用了GP先验,然后通过压缩这个链接函数去获得概率性的分类。潜在函数 f 也被称为损害函数,其值是不会被观察的,并且与自身没有关联。这样的目的是为了能够方便地格式化模型,并且在预测中也去除了 f **(集成并提取出来)。GPC实现了logistic链接函数,虽然其积分不能被分析与计算,但是对于二元分类问题来说却很容易获得其近似分类。
与在上面章节的回归设置里不同,其潜在函数** f **的后验对GP先验来说不是高斯的,因为高斯似然无法适用于离散型的标签。所以正好相反,一个非高斯似然是用到了logistic链接函数(logit)的。GPC使用基于拉普拉斯逼近的高斯来逼近其非高斯后验。如果想要知道更多的细节的话可以查看[RW2006]的第三章。
GP的先验均值在默认情况下被初始化为0。然后先验的协方差可以通过核对象来赋值。核的超参数会在GPR拟合最大化LML的过程中,通过传递** optimizer 参数来调优。不过LML可能会有多个局部最优值,所以需要设置 n_restarts_optimizer 参数来反复执行以获得一个稳定的最优值。在第一次运行的过程中通常会从初始化核的超参数值来开始;然后则从可选的值域里随机挑出超参数的值。如果要保持初始化的超参数的值,可以往参数 optimizer 传入 None **。
GaussianProcessClassifier
通过执行基于一对多或一对一的训练和预测来支持多类分类。在一对多的情况,一元GPC会对每个类进行训练,将每一类区分开来。在一对一的情况下,一元GPC会对每一对类进行训练,将其分成两类。然后再讲这些单个预测结果组合成多元分类。要了解更多的细节的话,可以查看多元分类一节。
在GPC里,一对一或许有着更廉价的计算能力,因为它只需要解决数据集中子集的大多数问题(预测出子集的大部分类),而不是解决整个数据集中的较少部分问题(预测出整个数据集的少部分类)。因为GPC把数据集以立方的方式缩放,这样也许会有着更快的处理速度。但是,要注意的是一对一并不支持预测概率估计,而是只支持平面预测。更进一步的,GaussianProcessClassifier
(目前)还没有在内部实现一个多类的拉普拉斯近似算法,而是使用了上面讨论的那种方法在内部来解决多元分类任务,其结合了一对多和一对一这两种方式。
1.7.4. GPC的一些例子#
1.7.4.1. GPC的概率预测##
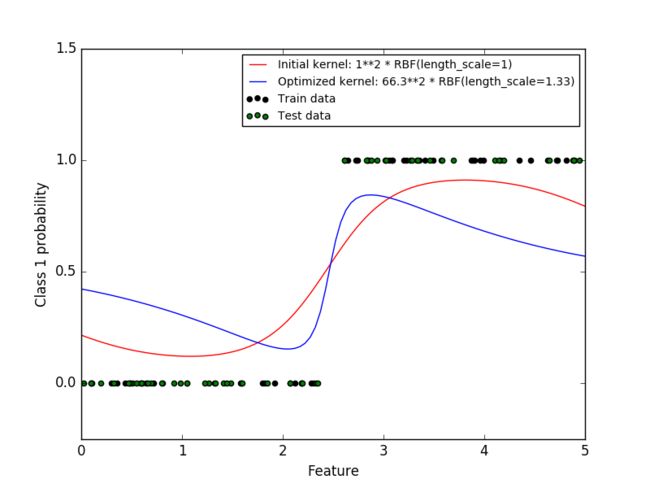
这个例子描绘了GPC在RBF有不同的超参数选择下进行的概率预测。第一个图表展示了GPC在任意超参数下的概率预测,并且其超参数对应着最大边际似然(LML)。
虽然由最优LML选出的超参数有着较大的LML,因为他们根据测试数据的对数误差会有略差的表现。这个图表显示,因为在类边界有一个陡峭的类概率变化(这一点是好的),但是预测出的概率却总是接近0.5(这一点并不好)。这种不好的影响的成因是GPC内部所使用的拉普拉斯近似算法。
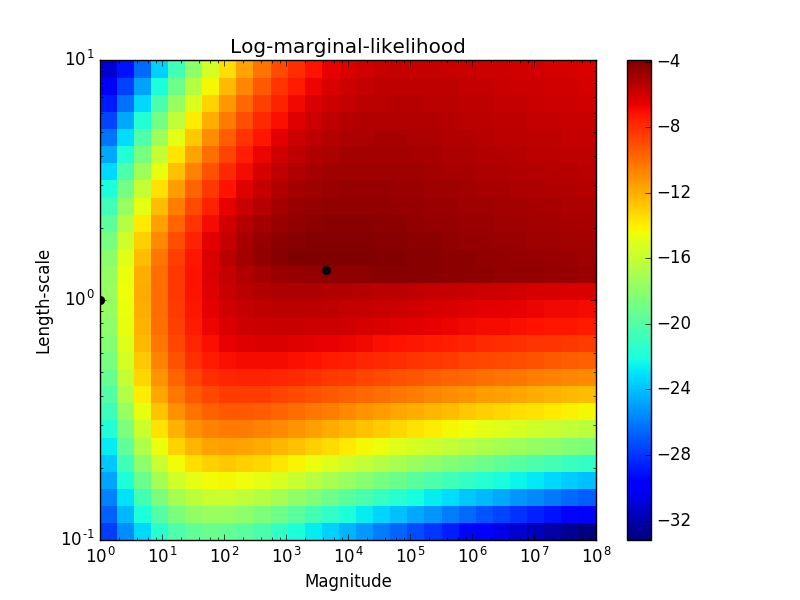
第二个图表展示了在不同核参数的情况下,对数边际似然的情况。使用黑点来显示在第一张图里所使用超参数组合。
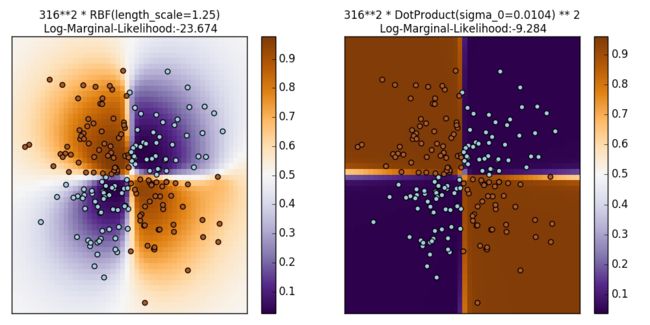
1.7.4.2. GPC在异或数据集##
这个例子展示了GPC对异或数据集的说明情况。通过固定各向同性核(RBF)和固定核(点乘)。在这个特定的数据集上,点乘核能够获得更好的结果,因为类边界是线性的,并且跟坐标轴重合。但是这个示例中,像 RBF 这种固定核却能够得到更好的效果。
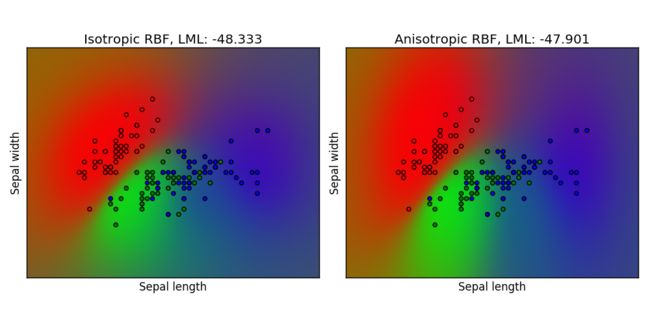
1.7.4.3. GPC在鸢尾花数据集##
这个示例展示了GPC在分别在各向同性和各向异性核的情况下,对二维版本的鸢尾花数据集上的概率估计。这个说明展示了GPC适用于非二元分类的情况(多元分类)。各向异性RBF核通过向两个特征维度分配不同的长度尺度来获得略高的对数边际似然。
1.7.5. 高斯过程的核#
核(在高斯过程的上下文里也被称为协方差函数)在高斯过程中是一个关键的部分,其决定了高斯过程先验和后验的形状。通过相似的数据点有着相似的目标值这一假设,与两个数据点之间的关系进行结合来定义出“相似度”,并以此来对已学习函数的假设进行编码。两种类型的核能够通过这些来进行区分:固定核只依赖两个数据点直接的距离,而不是他们的绝对值** k(xi, xj) = k(d(xi, xj)) **,从而在输入空间中的翻译不变;而非固定核相比于固定核,其也依赖于数据点的值。固定核能够更进一步的被细分成各项同性核和各向异性核,其中各向异性核在输入空间中的旋转是不变的。如果想要了解更多细节的话,可以建议查看[RW2006]的第四节。
1.7.5.1.
核 的一个主要用法是计算数据点之间,高斯过程的协方差。对此能够使用核里面的call方法。这个方法能够用来计算一个二维数组** X 内,所有数据点对的"自协方差",或计算二维数组 X 与二位数组 Y 中,其各自数据点的组合的"交叉协方差"。下面的等式对所有核 k 内恒为真(除了白核)k(X) == K(X, Y=X)**。
如果只需要使用"自协方差"的对角线,那么可以使用核里面的** diag() 函数,这个函数比起直接调用 call 的话计算效率要更高一些:np.diag(k(X, X)) == k.diag(X)**。
核通过超参数向量** θ 来实现参数化。这些超参数控制着实例的长度尺度,或核的周期性(下方有提到)。所有的核都支持计算其核相对于 θ 的自协方差的分析梯度,只需要在 call 方法里设置 eval_gradient=True **即可。
梯度在高斯过程(回归器与分类器均有)中,计算对数边际似然的梯度中使用到,然后再反过来使用它来决定** θ 的值,即通过梯度上升来最大化对数边际似然来得到。对于每个超参数而言,在创建核的实例时,他们的初始值和边界都需要被指定。而这时候的 θ 值能够通过对核对象设置 theta 参数来设置。然后超参数的边界则是通过核的 bounds 参数来设置。不过要注意的是,这两个属性(theta** 和 bounds)在更适合基于梯度的优化时,他们返回的值则是内部的对数转换值。每个超参数的指定值都会被存储到各自对应的核实例里的参数。不过使用名词为** "x" **的超参数的核必须拥有参数 self.x 和 self.x_bounds。
所有核类的基本抽象类都是 Kernel 类。核内有一个与** Estimator 类似的实现,它提供了这些方法, get_params() **, ** set_params() 和 clone() 。这允许通过类似 管道(Pipeline) 或 网格搜索(GridSearch) 这些meta-估计器来设置核的值。但是由于核的嵌套结构(通过应用核运算符,下方有说明),核参数的名字也许会变的相对复杂一些。对于一般的二元核操作符,参数的左操作数的前缀是 k1__ ,而右操作数的前缀则是 k2__ 。一个额外的协方差函数是 clone_with_theta(theta) ,它返回一个参数为 theta **的克隆核。下面是一个代码说明的例子:
>>> from sklearn.gaussian_process.kernels import ConstantKernel, RBF
>>> kernel = ConstantKernel(constant_value=1.0, constant_value_bounds=(0.0, 10.0)) * RBF(length_scale=0.5, length_scale_bounds=(0.0, 10.0)) + RBF(length_scale=2.0, length_scale_bounds=(0.0, 10.0))
>>> for hyperparameter in kernel.hyperparameters: print(hyperparameter)
Hyperparameter(name='k1__k1__constant_value', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k1__k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
>>> params = kernel.get_params()
>>> for key in sorted(params): print("%s : %s" % (key, params[key]))
k1 : 1**2 * RBF(length_scale=0.5)
k1__k1 : 1**2
k1__k1__constant_value : 1.0
k1__k1__constant_value_bounds : (0.0, 10.0)
k1__k2 : RBF(length_scale=0.5)
k1__k2__length_scale : 0.5
k1__k2__length_scale_bounds : (0.0, 10.0)
k2 : RBF(length_scale=2)
k2__length_scale : 2.0
k2__length_scale_bounds : (0.0, 10.0)
>>> print(kernel.theta) # Note: log-transformed
[ 0. -0.69314718 0.69314718]
>>> print(kernel.bounds) # Note: log-transformed
[[ -inf 2.30258509]
[ -inf 2.30258509]
[ -inf 2.30258509]]
所有的高斯过程的核都是能够与 sklearn.metrics.pairwise
互操作的,反过来也一样:Kernel
派生类的实例能够作为一个** 度量 通过 sklearn.metrics.pairwise
传递到 pairwise_kernels(成对核)。更进一步的,成对核的核函数在通过包装器类 PairwiseKernel
后能够作为一个GP(高斯过程)核来使用。不过要注意的是,超参数的梯度不是分析型的,而是数值型,并且这些核只支持各向同性距离。参数 gamma **可以考虑看成是一项超参数,并且它是能够最优的。其他的核参数在初始阶段直接进行设置,并且其值保持固定。
1.7.5.2. 基本的核##
ConstantKernel(常量核) 能够作为乘积核(Product Kernel)的一部分,并且它可以对核内的其他因子进行缩放,而作为Sum 核 ,它可以修改高斯过程的均值。这个常量核依赖于** constant_value **这一参数。它的定义是:
白核 的一个主要用法是作为sum核的一部分,用来解释噪声分量。参数** noise_level **代表着估计过程中的噪声等级。它的定义是:
1.7.5.3. 核运算##
核运算是获取一个或两个基本核,然后通过组合他们来获得一个新的核。Sum
核需要两个核,k1 和 k2 ,然后通过k_sum(X, Y) = k1(X, Y) + k2(X, Y)来组合他们。Product
核需要两个核,**k1 和 k2 ,然后通过 k_product(X, Y) = k1(X, Y) * k2(X, Y) 来组合他们。Exponentiation(指数) 核需要一个基本核和一个标量参数 exponent ,然后通过 k_exp(X, Y) = k(X, Y) ^ exponent **来组合他们。
1.7.5.4. 径向基函数(RBF)核##
RBF 核是一种固定核。它也以"平方指数"核这一名称被人所知。这个核通过长度尺度** l > 0 来实现参数化,其中这个参数能够是一个标量(核的各项同性的变体)或是一个跟输入 x **有着相同维数的向量(核的各向异性的变体)。
这个核是无限可微的,这意味着如果RBF核作为高斯过程的协方差函数的话,则它拥有所有阶的均方导数,所以它的曲线非常平滑。从RBF核中产生的高斯过程的先验和后验如下图所示:
1.7.5.5. Matérn核##
Matern 是一种固定核,并且是 RBF
核的一种概况。它有着一个额外的参数** ν ,这个参数用来控制产生函数的平滑度。它通过长度尺度这一参数 l > 0 来实现参数化,这个参数能够是一个标量(核的各种各项同性的变体)或是一个跟输入 x **有相同维数的向量(核的各种各项异性的变体)。
当** ν -> ∞ 时,Matérn核则收敛成RBF核。当 ν = 1/2 **时,Matérn核则变得跟绝对指数核一样,即:
尤其是** ν = 3/2 **时,
或** ν = 5/2 **
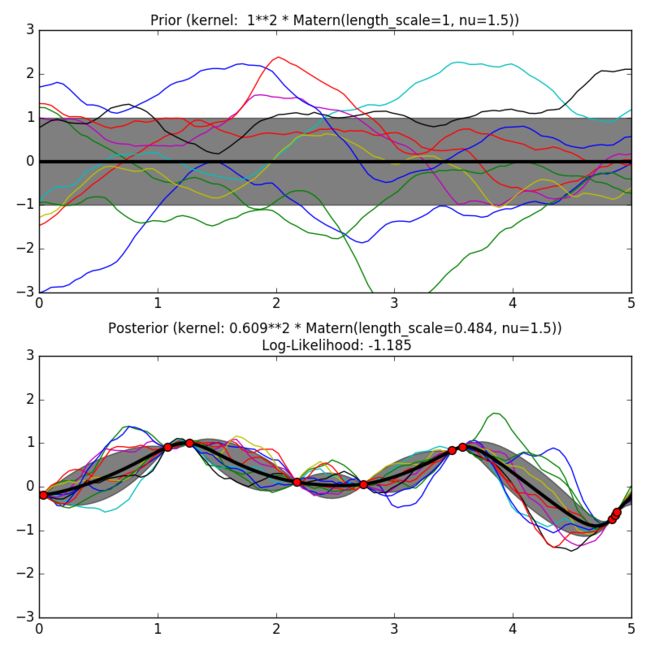
这些在学习函数中都是挺受欢迎的选项,虽说这些不是无限可微的(跟RBF核的定义一样),但是也至少出现一次微分(ν = 3/2)或者是两次微分(ν = 5/2)。通过** ν **控制学习函数的平滑性的这一灵活性,使得其能够适应真实的底层函数。从Matérn核中产生的高斯过程的先验和后验如下图所示:
[RW2006]中的第84页有着关于Matérn内核的不同变体的进一步细节。
1.7.5.6 二次有理核##
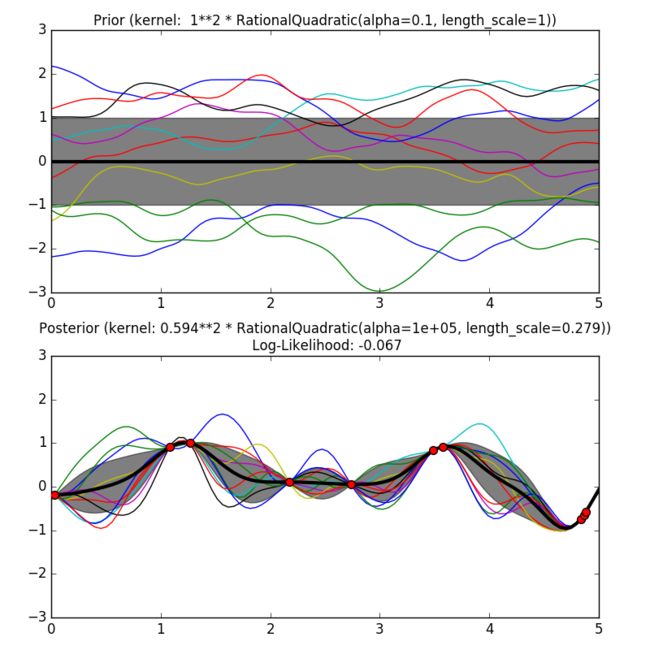
RationalQuadratic(二次有理核) 可以看成是RBF 核与各种具有不同特性的长度尺度参数的比例混合(无限和)。它通过长度尺度参数** l > 0 和比例混合参数 α > 0 来参数化的。但是目前仅支持 l **是标量的各项同性变量。
从二次有理核中产生的高斯过程的先验和后验如下图所示:
1.7.5.1. 指数正弦平方核##
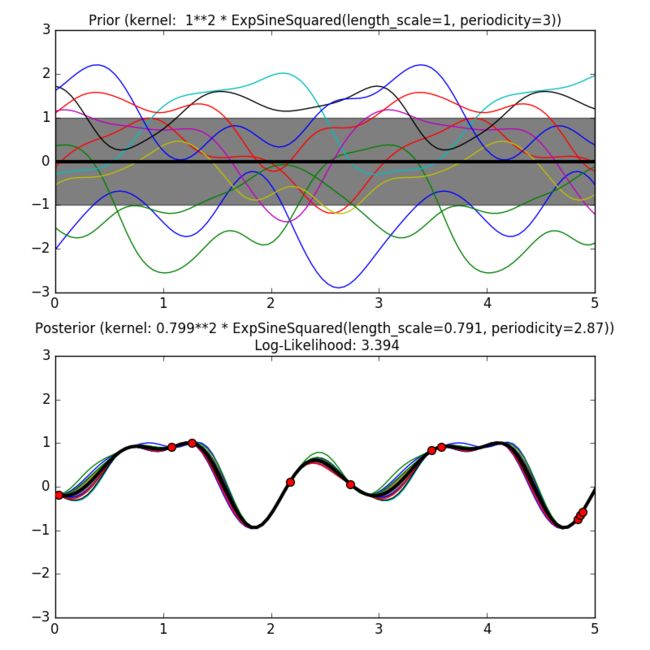
ExpSineSquared(指数正弦平方核) 允许模型化周期函数。它通过长度尺度参数** l > 0 与周期参数 p > 0 来参数化。目前仅支持 l **是标量的各项同性变量。
从指数正弦平方核中产生的高斯过程的先验和后验如下图所示:
1.7.5.8. 点乘核##
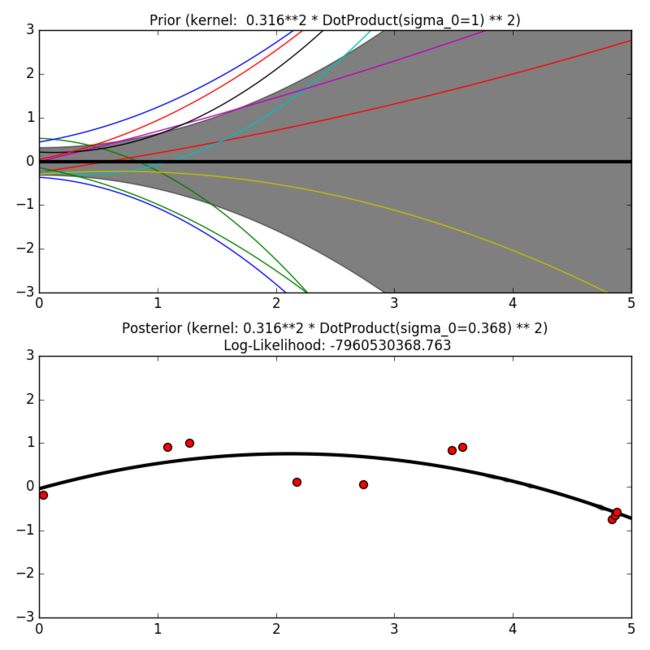
DotProduct(点乘核) 是一种非固定核,通过设置先验** N(0,1) 于系数 x_d(d = 1, ..., D) 和设置先验 N(0, σ_0 ^ 2) 与偏值上的一个线性回归来获得。点乘核 在坐标上对于原点的旋转是不变的,但是转换就不是了。它通过参数 σ_0 ^ 2 来参数化。当 σ_0 ^ 2 = 0 时,这个核可以称之为齐次线性核,反之当 σ_0 ^ 2 不等于0 **时则是非齐次线性核。
点乘核 一般跟取幂组合。下面是在指数为2时的一个例子:
1.7.5.9. 参考文献##
- [RW2006] Gaussian Processes for Machine Learning, Carl Eduard Rasmussen and Christopher K.I. Williams, MIT Press 2006. Link to an official complete PDF version of the book here .
1.7.6. 传统高斯过程#
在这一节,下面所描述的高斯过程的实现是scikit-learn 0.16.1的版本。但是要注意的是这个实现已经被弃用,并且会在0.18版本里去除。
1.7.6.1. 一个介绍性的回归例子##
假设我们想要一个** g(x) = xsin(x) **这样的替代函数。为了做到这一点,这个函数将会在实验设计上进行评估。然后我们定义出一个高斯处理模型,再使用一些额外的参数来指定它是一个回归还是一个相关模型,然后再使用它来拟合数据。根据实例化过程中提供的参数数量,在拟合过程中可以选择使用参数的最大似然估计或者是参数本身。
>>> import numpy as np
>>> from sklearn import gaussian_process
>>> def f(x):
... return x * np.sin(x)
>>> X = np.atleast_2d([1., 3., 5., 6., 7., 8.]).T
>>> y = f(X).ravel()
>>> x = np.atleast_2d(np.linspace(0, 10, 1000)).T
>>> gp = gaussian_process.GaussianProcess(theta0=1e-2, thetaL=1e-4, thetaU=1e-1)
>>> gp.fit(X, y)
GaussianProcess(beta0=None, corr=,
normalize=True, nugget=array(2.22...-15),
optimizer='fmin_cobyla', random_start=1, random_state=...
regr=, storage_mode='full',
theta0=array([[ 0.01]]), thetaL=array([[ 0.0001]]),
thetaU=array([[ 0.1]]), verbose=False)
>>> y_pred, sigma2_pred = gp.predict(x, eval_MSE=True)
1.7.6.2. 拟合带噪声的数据##
当要拟合的数据携带有噪声时,可以通过为每个点额外设置一个噪声方差的方式来使用高斯过程。GaussianProcess 带有一个叫** nugget **的参数,它被用来添加进由训练点组成的相关矩阵中的对角线内:其实就是一种 Tikhonov 正则化。但是在平方指数相关函数上,使用这种正则化方式等价于在输入中指定一个分数的方差(也就是下图这种形式了):
当 nugget 和 ** corr **这两个参数被设置为合适的值时,高斯过程就能够从带噪声的数据上稳健地提取出一个潜在的可用函数。
1.7.6.3. 数学公式##
1.7.6.3.1. 原始假设###
假设有人想要对计算机的实验输出进行建模,然后其定义了一个公式:
GPML(Gaussian Processes for Machine Learning)则从这假设开始,
假设这个函数是高斯过程** G **的一个条件样本路径,所以其形式可变为:
其中** f(X)^T·β ** 是一个线性模型,然后** Z(X) **是一个带有完全静态协方差的一个零均值高斯过程:
其中** σ^2 为方差,R **为相关函数,并且这个函数只依赖每个样本或特征之间的绝对相对距离。
对这个基本公式来说,GPML只不过是一个基本最小二乘线性回归问题的一个扩展:
除了我们通过相关函数来额外假设样本之间的空间一致性外,是生死啊哈那个,平台的最小二乘法假设了模型** R(|X - X|) **在 ** X = X 的情况下结果为1,否则为0:
这种模型被称为 dirac 相关模型,不过有时也被称为 kriging 文献中所涉及的 nugget **相关模型。
1.7.6.3.2 最优线性无偏预测(BLUP)###
现在我们从观测结果的样本路径** g **来推导出其最优线性无偏预测。
这种预测是通过这些属性所派生出来的:
- 线性(或观察结果的线性组合)
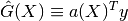
- 是无偏的(即无偏值bias)
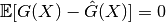
- 在极值(在均方误差均值上)
所以这个预测的最佳权重向量 a(X) 是下式的解:
然后再用拉格朗日来重写这个公式来解出最优值,然后结果应该就是我们所预测的闭合解 -- 详细的证明过程在下面给出:
所以最后BLUP的显示形式为带均值的高斯随机变量:
以及它的方差:
要说明的有:
- 相关矩阵的项(** Ri·j )是通过关于其自相关函数和它的内置参数 θ **定义的:
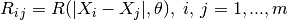
- 预测点与DOE点之间的互相关向量(** ri **):
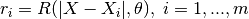
- 回归矩阵(** Fi·j )(如果 f **为多项式偏值的话,这个矩阵就为Vandermonde矩阵)
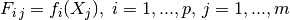
- 泛化的最小二乘回归权重(β):
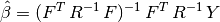
- 向量
不过要注意的是高斯过程的预测器做出的概率估计这一操作过程是一个全分析,且大多过程都依赖于基本线性运算。更准确地说,均值预测是两个简单线性的组合(点乘),然后其方差需要两个逆矩阵,但是只有在使用Cholesky的分解算法时,相关矩阵才能够被分解。
1.7.6.3.3. 经验性最优线性无偏预测(EBLUP)###
现在,我们从上述假设中知道了自相关和回归模型。但是事实上,我们并不总是能够提前知道这些的,因此需要一个方法来根据模型能否做出积极的经验判断来选择模型。
若需要做到这点则需要涉及到BLUP的一些剩余的未知参数了。所以为了做到这一点,一个结合了观察结果和一些推断理论的方法出现了。这个方法的目前实现是基于DACE的Matlab工具箱中的最大似然估计 -- 可以查看DACE手册中有关这一公式的说明。然后在其自相关参数上的求最大似然估计就相当于一个求全局最优值问题,然后这个全局最优值是通过 scipy.optimize 的 fmin_cobyla 优化函数来求解的。但是在面对各向异性问题时,这可以使用Welch的分量优化算法,详细情况可以查看下方的参考
1.7.6.4. 相关模型##
一般的相关模型都可以跟一些有名的SVM核互相匹配,那是因为这些模型大多数都是基于等式所定义的。并且他们也必须是固定且满足Mercer条件。不过要注意的是,相关模型的置信选择应该是从观察结果的原始实验中的已知条件所做出的。例如:
- 如果原始实验是无限可微的(平滑),那么就应该使用平方指数的相关模型
- 如果不是无限可微的,那就一个使用指数相关模型。
- 还有需要注意的是,这里还有一种相关模型是取度的可导性作为输入,这种模型称为Matern相关模型,但是在此处并没有对其进行实现(待做)。
如果想要关于这些的更详细的讨论,可以查看引用中由Rasmussen & Williams所著的书
1.7.6.5. 回归模型##
一般线性回归模型涉及到零(常数),一阶和二阶多项式。但是有一种是通过输入他的Python函数形式,然后输入特征X,结果再返回一个包含函数集的向量。不过这种方法的限制是,函数的数量不能超过结果值的数量,因此这种潜在的回归是不确定的。
1.7.6.6. 实现细节##
这个类的实现是基于DACE Matlab工具箱而成的:
引用####
- DACE, A Matlab Kriging Toolbox S Lophaven, HB Nielsen, J Sondergaard 2002,
- W.J. Welch, R.J. Buck, J. Sacks, H.P. Wynn, T.J. Mitchell, and M.D. Morris (1992). Screening, predicting, and computer experiments. Technometrics, 34(1) 15–25.
(在尝试翻译这篇文档的时候难免会因为各种问题而出现错翻,如果发现的话,烦请指出,谢谢> <)