模拟退火是对热力学退火过程的模拟,在某一给定初温下,通过缓慢下降温度参数,使算法能够在多项式时间内给出一个近似最优解。本质上也是蒙特卡洛算法。作为一种比较简单的智能算法,能以较高的效率解决优化问题,如求最值,tsp问题等。
本文就以旅行商问题为例实现一下:
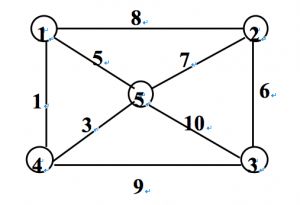
旅行家要旅行下面5个城市,要求各个城市经历且仅经历一次然后回到出发城市,并要求所走的路程最短。每条边上的值表示它们的间隔距离。端点的值时城市的序号。
先写入数据
n=5;
表示有5个城市。
len=[0,8,inf,1,5; 8,0,6,inf,7; inf,6,0,9,10; 1,inf,9,0,3; 5,7,10,3,0];
第i行,j列第值就表示城市i到城市j的距离
随便设置一个初始温度temperature,还有迭代次数m:
temperature=100*n;
m=100;
while temperature>0.0001 %0.0001也不是固定的,根据题目选择合适的结束温度即可
for i=1:m
在这里进行模拟退火,在后面详细写出
end
循环内部:
先计算初始情况的旅行长度lens1
lens1=0;
for i=1:n-1
lens1=lens1+len(city(i),city(i+1));
end
lens1=lens1+len(city(n),city(1));
接着写一个随机交换城市顺序的函数
function city=SA_testupdate(city,n)
p1=floor(1+n*rand());
p2=floor(1+n*rand());
while p1==p2
p1=floor(1+n*rand());
p2=floor(1+n*rand());
end
tmp=city(p1);
city(p1)=city(p2);
city(p2)=tmp;
end
再计算交换顺序后的旅行长度
lens2=0;
for i=1:n-1
lens2=lens2+len(tmp_city(i),tmp_city(i+1));
end
lens2=lens2+len(tmp_city(n),tmp_city(1));
敲黑板!这里是重点!!!!
d=lens2-lens1; %新老距离的差值
if d<0 %如果新路线好于旧路线,用新路线代替旧路线
city=tmp_city;
else %温度越低,新老距离差值越大,越不太可能接受新解
if exp(-d/temperature)>rand() %以概率选择是否接受新解
city=tmp_city; %接受的新解不一定是最优解
end
end
别忘了还要不断降低温度
temperature=temperature*0.99;
然后就可以得到
数组city,存放着最优的路线。这题我数据没有凑好,有好几种结果
lens(end),为最优路线的长度。这题的答案是16
最后还是汇总一下代码:
SA_test.m中:
clear all;
n=5;
len=[0,4,inf,1,5; 4,0,7,inf,6; inf,7,0,3,2; 1,inf,3,0,9; 5,6,2,9,0];
city=struct([]);
city=1:5;
l=1; %统计迭代次数
temperature=100*n; %初始温度
m=100; %内部蒙特卡洛循环迭代次数
while temperature>0.0001 %停止迭代温度
for i=1:m %多次迭代
lens1=0;
for i=1:n-1
lens1=lens1+len(city(i),city(i+1));
end
lens1=lens1+len(city(n),city(1));
tmp_city=SA_testupdate(city,n); %产生随机扰动
lens2=0;
for i=1:n-1
lens2=lens2+len(tmp_city(i),tmp_city(i+1));
end
lens2=lens2+len(tmp_city(n),tmp_city(1));
d=lens2-lens1; %新老距离的差值
if d<0 %新路线好于旧路线,用新路线代替旧路线
city=tmp_city;
else %温度越低,新老距离差值越大,越不太可能接受新解
if exp(-d/temperature)>rand() %以概率选择是否接受新解
city=tmp_city; %接受的新解不一定是最优解
end
end
end
l=l+1;
lens(l)=0;%计算新路线距离
for i=1:n-1
lens(l)=lens(l)+len(city(i),city(i+1));
end
lens(l)=lens(l)+len(city(n),city(1));
temperature=temperature*0.99; %温度不断下降
end
city
lens(end)
SA_testupdate.m中:
function city=SA_testupdate(city,n)
%随机交换顺序
p1=floor(1+n*rand());
p2=floor(1+n*rand());
while p1==p2
p1=floor(1+n*rand());
p2=floor(1+n*rand());
end
tmp=city(p1);
city(p1)=city(p2);
city(p2)=tmp;
end