问题
你想要运用逻辑回归分析。
方案
逻辑回归典型使用于当存在一个离散的响应变量（比如赢和输）和一个与响应变量（也称为结果变量、因变量）的概率或几率相关联的连续预测变量的情况。它也适用于有多个预测变量的分类预测。
假设我们从内置的mtcars数据集的一部分开始，像下面这样，我们将vs作为响应变量，mpg作为一个连续的预测变量，am作为一个分类（离散）的预测变量。
data(mtcars)
dat <- subset(mtcars, select=c(mpg, am, vs))
dat
#> mpg am vs
#> Mazda RX4 21.0 1 0
#> Mazda RX4 Wag 21.0 1 0
#> Datsun 710 22.8 1 1
#> Hornet 4 Drive 21.4 0 1
#> Hornet Sportabout 18.7 0 0
#> Valiant 18.1 0 1
#> Duster 360 14.3 0 0
#> Merc 240D 24.4 0 1
#> Merc 230 22.8 0 1
#> Merc 280 19.2 0 1
#> Merc 280C 17.8 0 1
#> Merc 450SE 16.4 0 0
#> Merc 450SL 17.3 0 0
#> Merc 450SLC 15.2 0 0
#> Cadillac Fleetwood 10.4 0 0
#> Lincoln Continental 10.4 0 0
#> Chrysler Imperial 14.7 0 0
#> Fiat 128 32.4 1 1
#> Honda Civic 30.4 1 1
#> Toyota Corolla 33.9 1 1
#> Toyota Corona 21.5 0 1
#> Dodge Challenger 15.5 0 0
#> AMC Javelin 15.2 0 0
#> Camaro Z28 13.3 0 0
#> Pontiac Firebird 19.2 0 0
#> Fiat X1-9 27.3 1 1
#> Porsche 914-2 26.0 1 0
#> Lotus Europa 30.4 1 1
#> Ford Pantera L 15.8 1 0
#> Ferrari Dino 19.7 1 0
#> Maserati Bora 15.0 1 0
#> Volvo 142E 21.4 1 1
连续预测变量，离散响应变量
如果数据集有一个离散变量和一个连续变量，并且连续变量离散变量概率的预测器（就像直线回归中x可以预测y一样，只不过是两个连续变量，而逻辑回归中被预测的是离散变量），逻辑回归可能适用。
下面例子中，mpg是连续预测变量，vs是离散响应变量。.
# 执行逻辑回归 —— 下面两种方式等效
# logit是二项分布家族的默认模型
logr_vm <- glm(vs ~ mpg, data=dat, family=binomial)
logr_vm <- glm(vs ~ mpg, data=dat, family=binomial(link="logit"))
查看模型信息：
# 输出模型信息
logr_vm
#>
#> Call: glm(formula = vs ~ mpg, family = binomial(link = "logit"), data = dat)
#>
#> Coefficients:
#> (Intercept) mpg
#> -8.8331 0.4304
#>
#> Degrees of Freedom: 31 Total (i.e. Null); 30 Residual
#> Null Deviance: 43.86
#> Residual Deviance: 25.53 AIC: 29.53
# More information about the model
summary(logr_vm)
#>
#> Call:
#> glm(formula = vs ~ mpg, family = binomial(link = "logit"), data = dat)
#>
#> Deviance Residuals:
#> Min 1Q Median 3Q Max
#> -2.2127 -0.5121 -0.2276 0.6402 1.6980
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -8.8331 3.1623 -2.793 0.00522 **
#> mpg 0.4304 0.1584 2.717 0.00659 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 43.860 on 31 degrees of freedom
#> Residual deviance: 25.533 on 30 degrees of freedom
#> AIC: 29.533
#>
#> Number of Fisher Scoring iterations: 6
画图
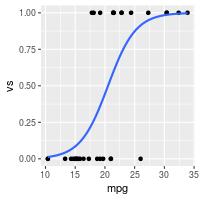
我们可以使用ggplot2或者基本图形绘制数据和逻辑回归结果。
library(ggplot2)
ggplot(dat, aes(x=mpg, y=vs)) + geom_point() +
stat_smooth(method="glm", method.args=list(family="binomial"), se=FALSE)
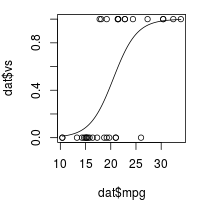
par(mar = c(4, 4, 1, 1)) # 减少一些边缘使得图形显示更好些
plot(dat$mpg, dat$vs)
curve(predict(logr_vm, data.frame(mpg=x), type="response"), add=TRUE)
plot of chunk unnamed-chunk-4
plot of chunk unnamed-chunk-4
离散预测变量，离散响应变量
这个跟上面的操作大致相同，am是一个离散的预测变量，vs是一个离散的响应变量。
# 执行逻辑回归
logr_va <- glm(vs ~ am, data=dat, family=binomial)
# 打印模型信息
logr_va
#>
#> Call: glm(formula = vs ~ am, family = binomial, data = dat)
#>
#> Coefficients:
#> (Intercept) am
#> -0.5390 0.6931
#>
#> Degrees of Freedom: 31 Total (i.e. Null); 30 Residual
#> Null Deviance: 43.86
#> Residual Deviance: 42.95 AIC: 46.95
# More information about the model
summary(logr_va)
#>
#> Call:
#> glm(formula = vs ~ am, family = binomial, data = dat)
#>
#> Deviance Residuals:
#> Min 1Q Median 3Q Max
#> -1.2435 -0.9587 -0.9587 1.1127 1.4132
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -0.5390 0.4756 -1.133 0.257
#> am 0.6931 0.7319 0.947 0.344
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 43.860 on 31 degrees of freedom
#> Residual deviance: 42.953 on 30 degrees of freedom
#> AIC: 46.953
#>
#> Number of Fisher Scoring iterations: 4
画图
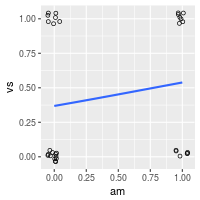
尽管图形可能会比连续预测变量的信息少，我们还是可以使用ggplot2或者基本图形绘制逻辑数据和回归结果。因为数据点大致在4个位置，我们可以使用抖动点避免叠加。
library(ggplot2)
ggplot(dat, aes(x=am, y=vs)) +
geom_point(shape=1, position=position_jitter(width=.05,height=.05)) +
stat_smooth(method="glm", method.args=list(family="binomial"), se=FALSE)
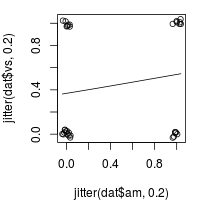
par(mar = c(4, 4, 1, 1)) # 减少一些边缘使得图形显示更好些
plot(jitter(dat$am, .2), jitter(dat$vs, .2))
curve(predict(logr_va, data.frame(am=x), type="response"), add=TRUE)
plot of chunk unnamed-chunk-7
plot of chunk unnamed-chunk-7
连续和离散预测变量，离散响应变量
这跟先前的例子相似，这里mpg是连续预测变量，am是离散预测变量，vs是离散响应变量。
logr_vma <- glm(vs ~ mpg + am, data=dat, family=binomial)
logr_vma
#>
#> Call: glm(formula = vs ~ mpg + am, family = binomial, data = dat)
#>
#> Coefficients:
#> (Intercept) mpg am
#> -12.7051 0.6809 -3.0073
#>
#> Degrees of Freedom: 31 Total (i.e. Null); 29 Residual
#> Null Deviance: 43.86
#> Residual Deviance: 20.65 AIC: 26.65
summary(logr_vma)
#>
#> Call:
#> glm(formula = vs ~ mpg + am, family = binomial, data = dat)
#>
#> Deviance Residuals:
#> Min 1Q Median 3Q Max
#> -2.05888 -0.44544 -0.08765 0.33335 1.68405
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -12.7051 4.6252 -2.747 0.00602 **
#> mpg 0.6809 0.2524 2.698 0.00697 **
#> am -3.0073 1.5995 -1.880 0.06009 .
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 43.860 on 31 degrees of freedom
#> Residual deviance: 20.646 on 29 degrees of freedom
#> AIC: 26.646
#>
#> Number of Fisher Scoring iterations: 6
有交互项的多个预测变量
当有多个预测变量时我们可能需要检验交互项。交互项可以单独指定，像a + b + c + a:b + b:c + a:b:c，或者它们可以使用a * b *c自动展开（这两种等效）。如果只是想指定部分可能的交互项，比如a与c有交互项，使用a + b + c + a:c。
# 执行逻辑回归，下面两种方式等效
logr_vmai <- glm(vs ~ mpg * am, data=dat, family=binomial)
logr_vmai <- glm(vs ~ mpg + am + mpg:am, data=dat, family=binomial)
logr_vmai
#>
#> Call: glm(formula = vs ~ mpg + am + mpg:am, family = binomial, data = dat)
#>
#> Coefficients:
#> (Intercept) mpg am mpg:am
#> -20.4784 1.1084 10.1055 -0.6637
#>
#> Degrees of Freedom: 31 Total (i.e. Null); 28 Residual
#> Null Deviance: 43.86
#> Residual Deviance: 19.12 AIC: 27.12
summary(logr_vmai)
#>
#> Call:
#> glm(formula = vs ~ mpg + am + mpg:am, family = binomial, data = dat)
#>
#> Deviance Residuals:
#> Min 1Q Median 3Q Max
#> -1.70566 -0.31124 -0.04817 0.28038 1.55603
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -20.4784 10.5525 -1.941 0.0523 .
#> mpg 1.1084 0.5770 1.921 0.0547 .
#> am 10.1055 11.9104 0.848 0.3962
#> mpg:am -0.6637 0.6242 -1.063 0.2877
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 43.860 on 31 degrees of freedom
#> Residual deviance: 19.125 on 28 degrees of freedom
#> AIC: 27.125
#>
#> Number of Fisher Scoring iterations: 7