转载:网络流基础篇——Edmond-Karp算法
网络流的相关定义:
- 源点:有n个点,有m条有向边,有一个点很特殊,只出不进,叫做源点。
- 汇点:另一个点也很特殊,只进不出,叫做汇点。
- 容量和流量:每条有向边上有两个量,容量和流量,从i到j的容量通常用c[i,j]表示,流量则通常是f[i,j].
通常可以把这些边想象成道路,流量就是这条道路的车流量,容量就是道路可承受的最大的车流量。很显然的,流量<=容量。而对于每个不是源点和汇点的点来说,可以类比的想象成没有存储功能的货物的中转站,所有“进入”他们的流量和等于所有从他本身“
出去”的流量。
- 最大流:把源点比作工厂的话,问题就是求从工厂最大可以发出多少货物,是不至于超过道路的容量限制,也就是,最大流。
求解思路:
首先,假如所有边上的流量都没有超过容量(不大于容量),那么就把这一组流量,或者说,这个流,称为一个可行流。
一个最简单的例子就是,零流,即所有的流量都是0的流。
- (1).我们就从这个零流开始考虑,假如有这么一条路,这条路从源点开始一直一段一段的连到了
汇点,并且,这条路上的每一段都满足流量<容量,注意,是严格的<,而不是<=。 - (2).那么,我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta,一定可以保证这个流依然是可行流,这是显然的。
- (3).这样我们就得到了一个更大的流,他的流量是之前的流量+delta,而这条路就叫做增广路。我们不断地从起点开始寻找增广路,每次都对其进行增广,直到源点和汇点不连通,也就是找不到增广路为止。
(4).当找不到增广路的时候,当前的流量就是最大流,这个结论非常重要。
补充:
(1).寻找增广路的时候我们可以简单的从源点开始做BFS,并不断修改这条路上的delta 量,直到找到源点或者找不到增广路。
(2).在程序实现的时候,我们通常只是用一个c 数组来记录容量,而不记录流量,当流量+delta 的时候,我们可以通过容量-delta 来实现,以方便程序的实现。
相关问题:
为什么要增加反向边?
在做增广路时可能会阻塞后面的增广路,
或者说,做增广路本来是有个顺序才能找完最大流的。
但我们是任意找的,为了修正,就每次将流量加在了反向弧上,让后面的流能够进行自我调整。
举例:
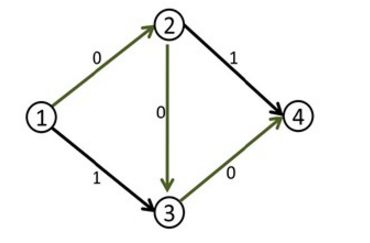
比如说下面这个网络流模型
我们第一次找到了1-2-3-4这条增广路,这条路上的delta值显然是1。
于是我们修改后得到了下面这个流。(图中的数字是容量)
这时候(1,2)和(3,4)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是1。
但是,
这个答案明显不是最大流,因为我们可以同时走1-2-4和1-3-4,这样可以得到流量为2的流。
那么我们刚刚的算法问题在哪里呢?
问题就在于我们没有给程序一个“后悔”的机会,应该有一个不走(2-3-4)而改走(2-4)的机制。
那么如何解决这个问题呢 ?
我们利用一个叫做反向边的概念来解决这个问题。即每条边(i,j)都有一条反向边(j,i),反向边也同样有它的容量。
我们直接来看它是如何解决的:
在第一次找到增广路之后,在把路上每一段的容量减少delta的同时,也把每一段上的反方向的容量增加delta。
c[x,y]-=delta;
c[y,x]+=delta;
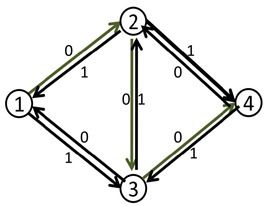
我们来看刚才的例子,在找到1-2-3-4这条增广路之后,把容量修改成如下:
这时再找增广路的时候,就会找到1-3-2-4这条可增广量,即delta值为1的可增广路。将这条路增广之后,得到了最大流2。
那么,这么做为什么会是对的呢?
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给“退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。
如果这里没有2-4怎么办?
这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点
同时本来在3-4上的流量由1-3-4这条路来“接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流。
A - Drainage Ditches
一道网络流裸题
- Edmonds_Karp 算法 邻接矩阵
#include
#include
#include
using namespace std;
const int MAXN=205;
const int INF=0x3f3f3f3f;
int graph[MAXN][MAXN];
int pre[MAXN];
int vis[MAXN];
int n,m;
int BFS(int st,int ed)
{
memset(vis,0,sizeof(vis));
queue que;
que.push(st);
vis[st]=1;
int curr,flow=INF;
pre[st]=pre[ed]=-1;
while(!que.empty())
{
curr=que.front();
que.pop();
if(curr==ed) break;
for(int nxt=1;nxt<=n;nxt++)
{
if(vis[nxt]==0&&graph[curr][nxt]!=0)
{
vis[nxt]=1;
if(flow>graph[curr][nxt]) flow=graph[curr][nxt];
pre[nxt]=curr;
que.push(nxt);
}
}
}
if(pre[ed]==-1) return 0;
return flow;
}
int Edmonds_Karp(int st,int ed)
{
int stream;
int sum=0;
while((stream=BFS(st,ed))!=0)
{
int u=ed;
while(pre[u]!=-1)
{
graph[pre[u]][u]-=stream;
graph[u][pre[u]]+=stream;
u=pre[u];
}
sum+=stream;
}
return sum;
}
int main()
{
int a,b,flow;
while(scanf("%d%d",&m,&n)!=EOF)
{
memset(graph,0,sizeof(graph));
while(m--)
{
scanf("%d%d%d",&a,&b,&flow);
graph[a][b]+=flow;
//注意,这里的a,b节点都是独一无二的节点(包含分裂的节点)
//比如原来有x个节点,通过分裂这x个节点构图,那么n=2*x,即有2*x个不同的节点
}
printf("%d\n",Edmonds_Karp(1,n));
}
}
- Edmonds_Karp算法 前向星
#include
#include
#include
#include
using namespace std;
const int MAXN=1010;
const int MAXE=5010;
const int INF=0x3f3f3f3f;
int head[MAXN],cnt;
struct Node
{
int to,next,val;
Node(){}
Node(int to,int next,int val):to(to),next(next),val(val){}
};
Node edge[MAXE];
void addEdge(int u,int v,int val)
{
edge[cnt]=Node(v,head[u],val);
head[u]=cnt++;
edge[cnt]=Node(u,head[v],0);
head[v]=cnt++;
}
int vis[MAXN],pre[MAXN];
int BFS(int st,int ed)
{
memset(vis,0,sizeof(vis));
vis[st]=1;
queue que;
que.push(st);
int u,v,flow=INF;
pre[st]=pre[ed]=-1;
while(!que.empty())
{
u=que.front();
que.pop();
if(u==ed) break;
for(int i=head[u];i!=-1;i=edge[i].next)
{
v=edge[i].to;
if(vis[v]==0&&edge[i].val>0)
{
vis[v]=1;
flow=min(flow,edge[i].val);
pre[v]=i;//注意寻路方式
que.push(v);
}
}
}
if(pre[ed]==-1) return 0;
return flow;
}
int Edmonds_Karp(int st,int ed)
{
int stream,flow=0;
while((stream=BFS(st,ed))!=0)
{ //pre通过节点存边的坐标,通过边的反向边的to获取上一个节点
for(int i=pre[ed];i!=-1;i=pre[edge[i^1].to])
{
edge[i].val-=stream;
edge[i^1].val+=stream;
}
flow+=stream;
}
return flow;
}
int main()
{
int a,b,n,m,flow;
while(scanf("%d%d",&m,&n)!=EOF)
{
memset(head,-1,sizeof(head));
cnt=0;
while(m--)
{
scanf("%d%d%d",&a,&b,&flow);
addEdge(a,b,flow);
}
printf("%d\n",Edmonds_Karp(1,n));
}
return 0;
}
Edmonds_Karp算法很难用邻接表描述,因为通过BFS得出一个pre数组,但是pre数组给出的某个顶点u和它的前一个顶点v,理论上我们要为v --> u 这条边减去相应的容量,u --> v这条边要添加相应的容量,但是我们不知道这两条边在邻接表的位置;解决办法有另开一个二维数组存储u-->v和v-->u在邻接表的位置,这样子还不如用邻接矩阵划算...
Ford_Fulkerson算法 邻接矩阵
#include
#include
#include
using namespace std;
const int INF=0x7fffffff;
const int MAXN=205;
int graph[MAXN][MAXN];
int vis[MAXN];
int n,m;
int dfs(int st,int ed,int f)
{
vis[st]=1;
if(st==ed) return f;
for(int i=1;i<=n;i++)
{
if(graph[st][i]>0&&vis[i]==0)
{
int d=dfs(i,ed,min(graph[st][i],f));
if(d>0)
{
graph[st][i]-=d;
graph[i][st]+=d;
return d;
}
}
}
return 0;
}
int Ford_Fulkerson(int st,int ed)
{
int flow=0,curr;
while(true)
{
memset(vis,0,sizeof(vis));
curr=dfs(st,ed,INF);
if(curr==0) return flow;
flow+=curr;
}
}
int main()
{
int a,b,val;
while(scanf("%d%d",&m,&n)!=EOF)
{
memset(graph,0,sizeof(graph));
while(m--)
{
scanf("%d%d%d",&a,&b,&val);
graph[a][b]+=val;
}
printf("%d\n",Ford_Fulkerson(1,n));
}
return 0;
}
- Ford_Fulkerson算法 邻接表
#include
#include
#include
#include
using namespace std;
const int INF=0x7fffffff;
const int MAXN=205;
struct Node
{
int to;
int flow;
int rev;//反向边在数组的位置
Node(){}
Node(int to,int flow,int rev):to(to),flow(flow),rev(rev){}
};
vector graph[MAXN];
int vis[MAXN];
int n,m;
void addEdge(int from,int to,int val)
{
graph[from].push_back(Node(to,val,graph[to].size()));
graph[to].push_back(Node(from,0,graph[from].size()-1));//反向边的流量为0
}
int dfs(int st,int ed,int f)
{
vis[st]=1;
if(st==ed) return f;
for(int i=0;i0)
{
int d=dfs(temp.to,ed,min(f,temp.flow));
if(d>0)
{
temp.flow-=d;
graph[temp.to][temp.rev].flow+=d;
return d;
}
}
}
return 0;
}
int Ford_Fulkerson(int st,int ed)
{
int flow=0,curr;
while(true)
{
memset(vis,0,sizeof(vis));
curr=dfs(st,ed,INF);
if(curr==0) return flow;
flow+=curr;
}
}
int main()
{
int a,b,val;
while(scanf("%d%d",&m,&n)!=EOF)
{
for(int i=1;i<=n;i++)
{
graph[i].clear();
}
while(m--)
{
scanf("%d%d%d",&a,&b,&val);
addEdge(a,b,val);
}
printf("%d\n",Ford_Fulkerson(1,n));
}
return 0;
}
- Ford_Fulkerson算法 前向星
#include
#include
using namespace std;
const int MAXN=210;
const int INF=0x7fffffff;
struct Node
{
int to;
int next;
int c;
};
Node Edge[MAXN*2];
int head[MAXN];
int vis[MAXN];
int cnt;
void addEdge(int u,int v,int val)
{
Edge[cnt].to=v;
Edge[cnt].c=val;
Edge[cnt].next=head[u];
head[u]=cnt++;
Edge[cnt].to=u;//添加反向边,流量为0
Edge[cnt].c=0;
Edge[cnt].next=head[v];
head[v]=cnt++;
}
int DFS(int st,int ed,int f)
{
vis[st]=1;
if(st==ed) return f;
for(int i=head[st];i!=-1;i=Edge[i].next)
{
if(Edge[i].c>0&&vis[Edge[i].to]==0)
{
int d=DFS(Edge[i].to,ed,min(Edge[i].c,f));
if(d>0)
{
Edge[i].c-=d;
Edge[i^1].c+=d;//添边的时候反向边正好在数组的相邻位置,所以i^1是取反向边
return d;
}
}
}
return 0;
}
int Ford_Fulkerson(int st,int ed)
{
int flow=0,d,u;
while(true)
{
memset(vis,0,sizeof(vis));
d=DFS(st,ed,INF);
if(d==0) break;
flow+=d;
}
return flow;
}
int main()
{
int n,m,a,b,val;
while(scanf("%d%d",&m,&n)!=EOF)
{
memset(head,-1,sizeof(head));
cnt=0;
while(m--)
{
scanf("%d%d%d",&a,&b,&val);
addEdge(a,b,val);
}
printf("%d\n",Ford_Fulkerson(1,n));
}
}
- Dinic算法 邻接矩阵
#include
#include
#include
#include
using namespace std;
const int INF = 0x7fffffff;
const int MAX = 205;
int c[MAX][MAX];
int step[MAX];
int n,m;
bool BFS(int st,int ed)
{
memset(step,-1,sizeof(step));
queue que;
step[st]=0;
que.push(st);
while(!que.empty())
{
int curr=que.front();
que.pop();
for(int i=1;i<=n;i++)
{
if(c[curr][i]>0&&(step[i]==-1))//i没访问过
{
step[i]=step[curr]+1;
if(i==ed) return true;
que.push(i);
}
}
}
return step[ed]!=-1;
}
int DFS(int st,int ed,int f)
{
if(st==ed||f==0) return f;
int flow=0,d;
for(int i=1;i<=n;i++)
{
if((step[i]==step[st]+1)&&c[st][i]>0&&(d=DFS(i,ed,min(c[st][i],f))))
{
c[st][i]-=d;
c[i][st]+=d;
flow+=d; //累加当前节点的某条路径的合适流量
f-=d; //当前节点的容量减去某条路径的合适流量
if(f==0) break; //如果当前节点的容量用完,说明无法再通过任何流量
}
}
if(flow==0) step[st]=INF;//如果当前节点无任何流量通过,取消标记
return flow;
}
int Dinic(int st,int ed)
{
int flow=0;
while(BFS(st,ed))
{
flow+=DFS(st,ed,INF);
}
return flow;
}
int main()
{
int a,b,flow;
while(scanf("%d%d",&m,&n)!=EOF)
{
memset(c,0,sizeof(c));
while(m--)
{
scanf("%d%d%d",&a,&b,&flow);
c[a][b]+=flow;
}
printf("%d\n",Dinic(1,n));
}
return 0;
}
- Dinic算法 邻接表
#include
#include
#include
#include
using namespace std;
const int INF = 0x7fffffff;
const int MAX = 205;
int step[MAX];
struct Node
{
int to;
int flow;
int rev;//记录反向边的index
Node(){}
Node(int to,int flow,int rev):to(to),flow(flow),rev(rev){}
};
vector graph[MAX];
int n,m;
void addEdge(int from,int to,int flow)
{
graph[from].push_back(Node(to,flow,graph[to].size()));
graph[to].push_back(Node(from,0,graph[from].size()-1));
}
bool BFS(int st,int ed)
{
memset(step,-1,sizeof(step));
queue que;
que.push(st);
step[st]=0;
while(!que.empty())
{
int curr=que.front();
que.pop();
for(int i=0;i0)
{
step[temp.to]=step[curr]+1;
if(temp.to==ed) return true;
que.push(temp.to);
}
}
}
return step[ed]!=-1;
}
int DFS(int st,int ed,int f)
{
if(st==ed||f==0) return f;
int flow=0;
for(int i=0;i0&&step[temp.to]==step[st]+1)
{
int d=DFS(temp.to,ed,min(f,temp.flow));
if(d>0)
{
temp.flow-=d;
graph[temp.to][temp.rev].flow+=d;
flow+=d; //累加当前节点的某条路径的合适流量
f-=d; //当前节点的容量减去某条路径的合适流量
if(f==0) break; //如果当前节点的容量用完,说明无法再通过任何流量
}
}
}
if(flow==0) step[st]=INF;//如果当前节点无任何流量通过,取消标记
return flow;
}
int Dinic(int st,int ed)
{
int flow=0;
while(BFS(st,ed))
{
flow+=DFS(st,ed,INF);
}
return flow;
}
int main()
{
int a,b,flow;
while(scanf("%d%d",&m,&n)!=EOF)
{
memset(graph,0,sizeof(graph));
while(m--)
{
scanf("%d%d%d",&a,&b,&flow);
addEdge(a,b,flow);
}
printf("%d\n",Dinic(1,n));
}
return 0;
}
- Dinic算法 前向星
#include
#include
#include
#include
using namespace std;
const int MAXN=1010;
const int INF=0x7fffffff;
struct Node
{
int to;
int next;
int c;
};
Node Edge[MAXN*2];//因为要建立反向边,所以边的数目要为两倍
int head[MAXN];
int step[MAXN];
int cnt;
void addEdge(int u,int v,int val)
{
Edge[cnt].to=v;
Edge[cnt].next=head[u];
Edge[cnt].c=val;
head[u]=cnt++;
Edge[cnt].to=u;
Edge[cnt].c=0;
Edge[cnt].next=head[v];
head[v]=cnt++;
}
bool BFS(int st,int ed)
{
queue que;
que.push(st);
memset(step,-1,sizeof(step));
step[st]=0;
int u,i;
while(!que.empty())
{
u=que.front();
que.pop();
for(i=head[u];i!=-1;i=Edge[i].next)
{
if(step[Edge[i].to]==-1&&Edge[i].c>0)
{
step[Edge[i].to]=step[u]+1;
que.push(Edge[i].to);
if(Edge[i].to==ed) return true;
}
}
}
return step[ed]!=-1;
}
int DFS(int st,int ed,int flow)
{
if(st==ed||!flow) return flow;
int curr=0;
for(int i=head[st];i!=-1;i=Edge[i].next)
{
if(step[st]+1==step[Edge[i].to]&&Edge[i].c>0)
{
int d=DFS(Edge[i].to,ed,min(Edge[i].c,flow));
if(d>0)
{
Edge[i].c-=d;
Edge[i^1].c+=d;//添反向边的时候是相邻的,i^1取相邻数;
curr+=d; //累加当前节点的某条路径的合适流量
flow-=d; //当前节点的容量减去某条路径的合适流量
if(flow==0) break;//如果当前节点的容量用完,说明无法再通过任何流量
}
}
}
if(curr==0) step[st]=INF;//如果当前节点无任何流量通过,取消标记
return curr;
}
int Dinic(int st,int ed)
{
int flow=0;
while(BFS(st,ed))
{
flow+=DFS(st,ed,INF);
}
return flow;
}
int main()
{
int n,m,a,b,val;
while(scanf("%d%d",&m,&n)!=EOF)
{
memset(head,-1,sizeof(head));
cnt=0;
while(m--)
{
scanf("%d%d%d",&a,&b,&val);
addEdge(a,b,val);
}
printf("%d\n",Dinic(1,n));
}
}