区块链概念的提出可以追溯到2008年Satoshi Nakamoto所发布的比特币白皮书:《Bitcoin: A Peer-to-Peer Electronic Cash System》。[1]
原文标题的“Electronic Cash”[2]一词,有别于通俗意义上的电子化的货币,比如:信用卡、借记卡,某银行间两个账户的转账,或者基于支付宝的在线支付交易。上述提及的之所以不能称为Electronic Cash,是因为它们不具备Cash的2个基本要素:匿名性和持有者之间线下交易的能力。[3]
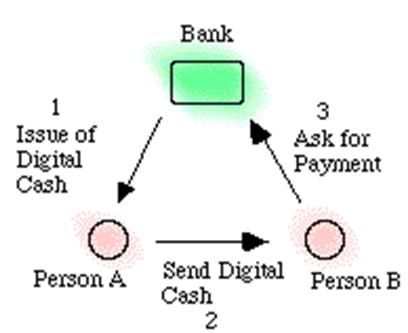
一个基于简易Electronic Cash System的交易过程大致如下:
- A在银行有1000.00 CNY的存款,A要求取出10.00 CNY,银行给A一个10.00 CNY的“硬币”(经过银行认证的、可以存储在电子邮件、USB等电子设备上),并且将A的余额修改为990.00 CNY。
- A把这张“硬币”通过网络发送给B,用于购买一杯咖啡。
- B收到“硬币”后验证钱是否是伪造的,如果验证通过,B会收下钱并交给A一杯咖啡,交易完成。
可以看到作交易双方的A和B并不需要知道任何对方的信息(即匿名性),也无需第三方的介入(即持有者之间线下交易),就完成了一次完整的交易过程。
然而,上述的过程有个很明显的问题:电子现金不具备现实中货币天然的防伪功能,A甚至通过简单的复制、黏贴就可以再造出与之前消费的一模一样的“硬币”,并将这笔钱再次用于购买另一款商品,这是数字现金中著名的Double-Spending问题。
为了解决这个问题,绝大部分文献都会在验证过程中引入一个可信的第三方,通常也就是银行。通过银行来记录A已经花费掉这个10.00 CNY硬币的事实,当A尝试第二次花费时,银行会拒绝认可该行为,从而防止Double-Spending的产生。
可以看到这是一种“中心化”的模式,银行是每一笔交易所必须要经过的中心节点,银行或者说可信第三方的引入很大程度上违背了上述数字现金的基本特性。那么,是否存在一种不依赖于中心机构的数字现金体系,让交易双方可以完成点对点的货币支付?
Satoshi Nakamoto通过他的白皮书提出了一个近乎完美的构思,并以“比特币”的形式将其付诸实践。区块链就是比特币支付体系中所涉及的底层技术之一。
区块链
要去掉前文所提及的对于银行的依赖,需要解决的问题就是B在收到“硬币”后如何验证“硬币”是否已经被花费过。银行本身通过对每笔交易记账(如果某个硬币消费过,就将硬币的状态标记为已消费)和查账(查看硬币消费状态)的方式来防止重复消费。如果B不需要跟银行直接通信就可以直接查询这样一个账本,在某种程度上就消除了部分对于银行的依赖(查账)。
而区块链承担的角色就是公开账簿,全网所有的节点通过查询这本账来判断某笔交易的合法性。
既然作为全网账簿,需要解决的本质问题就是公信力问题,其中一点就是:已有的交易纪录一旦记入账本就不可篡改,即使是“记账人员”本身也无法修改任意一条已存在的纪录。
一个简单的构思
假设区块就是某个时间段内若干条交易记录的简单集合,如何保证这个记录不可篡改?一个简单的做法就是哈希!一旦记录了区块的哈希值,试图修改其中任何一笔交易都会导致哈希值的变化,从而达到了防篡改的目的。
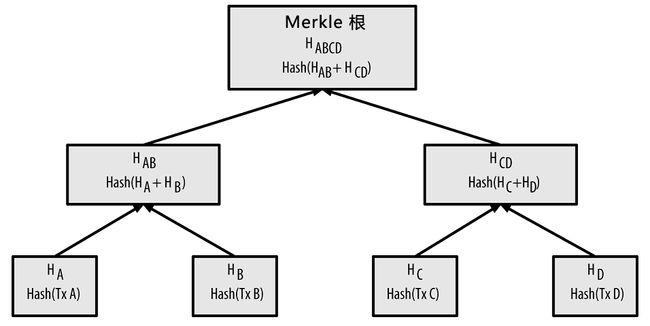
下图是比特币体系采用的Merkle树[4],通过对于交易TxA和TxB生成哈希HAB并通过与HCD的再次哈希得到树根HABCD,当客户端需要校验交易TxC是否存在于区块时,只需要对该交易做哈希生成HC并依次与HD和HAB依次取哈希值,再与树根的哈希值对比,如果一致则说明交易存在于区块中。这样的方式在白皮书中称为“Simplified Payment Verification”在算法上优于交易集合的遍历。
同时对于每个区块都需要加盖“时间戳”用以确定某个交易发生在某个时间点之前。
时间和哈希值共同保证了某一笔交易一旦入账则不可更改。
更近一步
上文通过Bn = H(tn, M(Txsn))的方式达到了某个区块防篡改的目的。其中tn表示区块n的时间戳, M(Txsn)表示交易合集的Merkle值,H表示哈希函数。“记账员”通过不停的对区块哈希并加盖时间戳来记账,一切看起来很完美。但是假设某一笔交易存在于时间戳为2016-11-11 01:00:00的区块,怎么保证另一笔存在于另一个区块的交易,实际上发生在2016-11-11 02:00:00,却不会被“记账员”因为某种利益偷偷把时间戳改成2016-11-11 00:00:00?上述的“记账员”对于时间拥有绝对权力,甚至可以随意更改任意一个区块的时间戳。需要有一个方法保证区块中纪录的每一笔交易都是按照时间顺序产生的。哪怕是“记账员”也不可以随意更改这个时间。[5]
假设我们在上述公式中引入因子Bn-1,则:Bn = H(tn, M(Txsn), Bn-1),其中:Bn-1 = H(tn-1, M(Txsn-1), Bn-2)
即新产生的区块需要引用上一个产生的区块的哈希值,区块间形成一个链条,B0->B1->...Bt-1->Bt->...->Bn,假设当前区块链已公布,要篡改纪录将某笔交易对应的区块插入Bt-1和Bt之间,势必需要在Bt-1之后插入Bt-1',并试图使Bt=H(tt, M(Txst), Bt-1'),根据哈希函数的性质,显然这是不可能的。同时假设要修改t-1时刻的某笔交易,势必导致Bt-1变化随后的所有区块的哈希值将会全部发生变化。
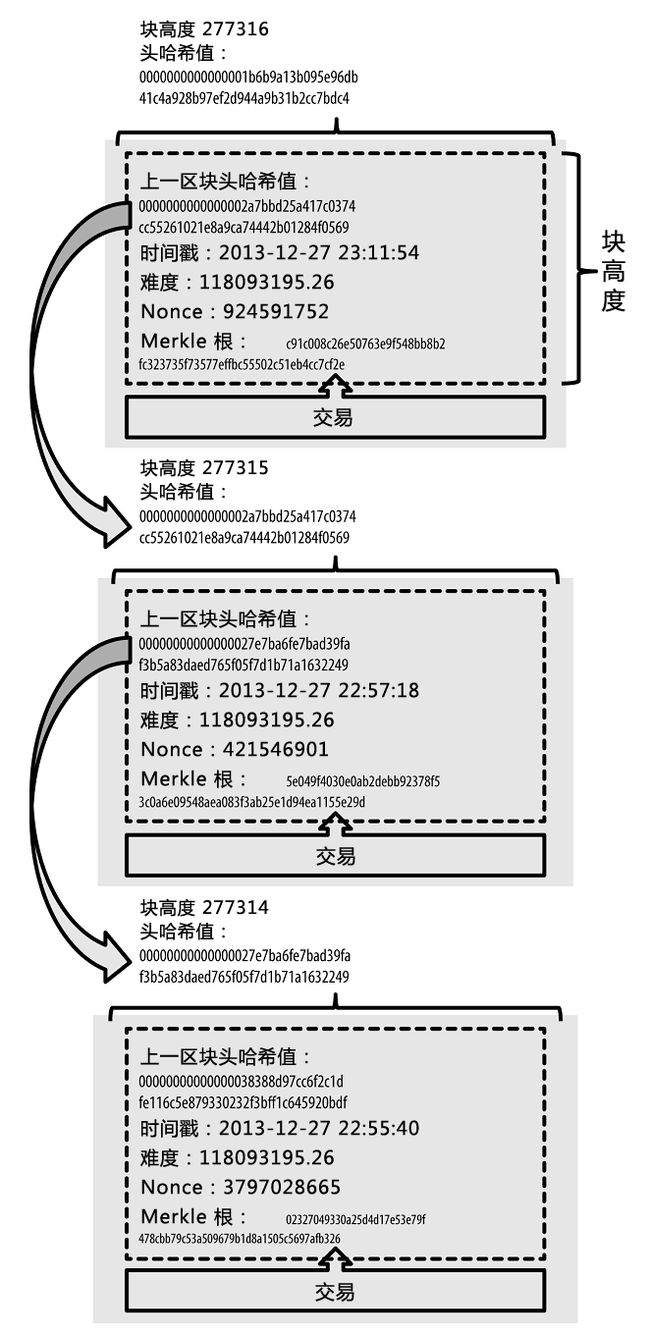
以下是真实的比特币系统中区块链的示意图[6]所示:
人人都是记账员
账本的问题解决了,客户端可以放心的查账,而且保证这本全网账簿是具有公信力的,那么如何产生账本的纪录,就成了下一个需要解决的问题。一旦解决了不依赖银行的记账问题,那么这种基于“记账员”的中心化的体系也就不再必要了。
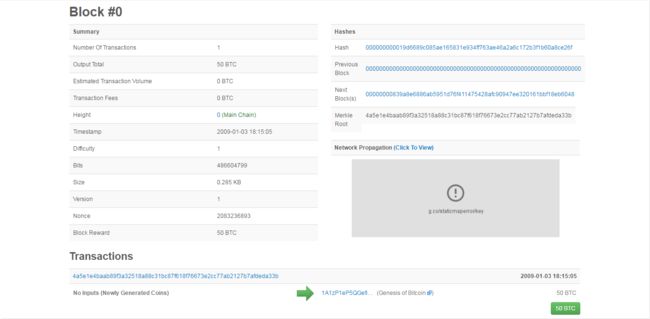
事实上,比特币网络中的每一个节点都有资格产生下一个合格的区块,也就是记账。所谓合格,即:从创世区块(区块链的第0个区块)开始,每个区块都对于下一个区块的哈希值有一个要求,已下图为例:
要求当下一个区块产生时,区块对应的哈希值必须 小于00000000839a8e6886ab5951d76f411475428afc90947ee320161bbf18eb6048这个数,如上述所说,计算区块的哈希B n = H(t n, M(Txs n), B n-1),如果结果不满足父区块的要求怎么办?在公式中,再引入一个干扰因子,则B n = H(t n, M(Txs n), B n-1, nonce),干扰因子的值从0开始一直累加,直到某个哈希值满足父区块的要求为止。
基于哈希函数的特性,从数学上来说上述过程只能通过穷举完成,也就是谁计算的速度快,谁就可以先得到合法的下一个区块,并通过P2P网络传播出去,其他矿工校验了这个区块的合法性后,将该区块加入到该矿工自己的内存中(一个完全的矿工节点在内存中存有从创世区块开始一直到当前时间所有的区块)。上述的过程称之为Proof-of-Work,即工作量证明,在比特币体系中有个形象的名词叫“挖矿”。
最长链
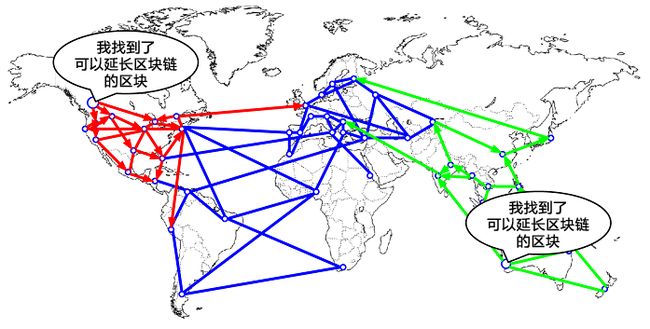
假设上一个合法区块要求子区块的哈希值满足小于H1,同时有两个节点,各自独立计算出了两个合法的哈希值均满足要求,此时就带来了一个新的问题,区块链分叉,[7]如下图所示:
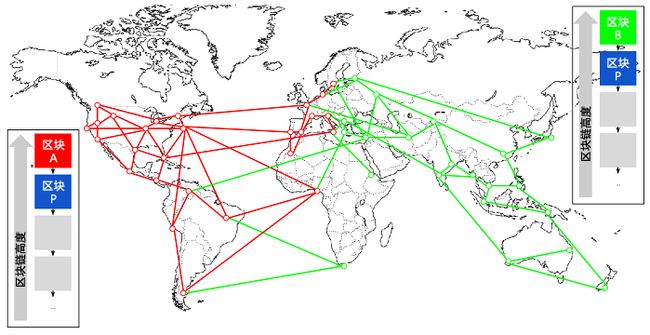
全网本来都基于蓝色区块链,接下来,全网节点分成2个阵营(红和绿)。
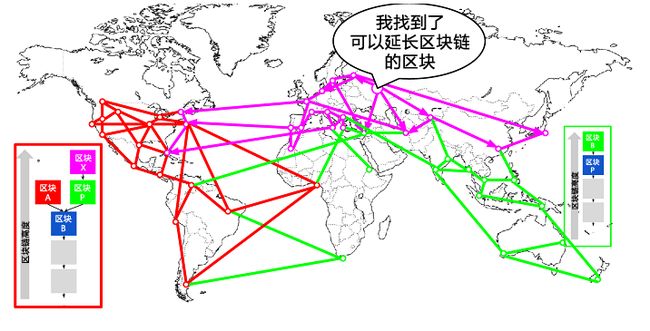
当前2个阵营都是合法的,因为他们完全符合区块链延伸的要求,同时两个阵营的区块链长度一致。除非保证两个阵营的算力永久平均分配,否则总有一个阵营抢在另一个阵营前发现工作量证明解并将其传播出去。在这个例子中我们可以打个比方,假如工作在“绿色”区块上的矿工找到了一个“粉色”区块延长了区块链(蓝色-绿色-粉色),他们会立刻传播这个新区块,整个网络会都会认为这个区块是有效的。
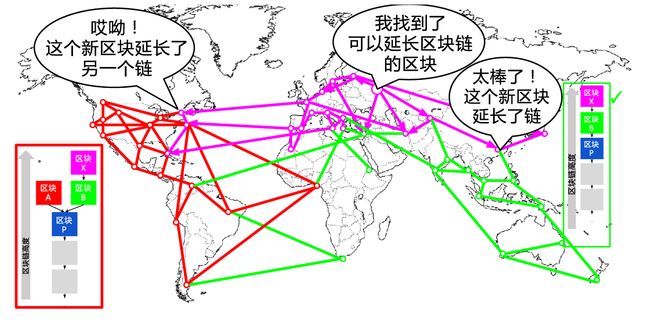
所有在上一轮选择“绿色”区块为胜出者的节点会直接将这条链延长一个区块。然而,那些选择“红色”区块为胜出者的节点现在会看到两个链:“蓝色-绿色-粉色”和“蓝色-红色”。如下图所示,这些节点会根据结果将“蓝色-绿色-粉色”这条链设置为主链,将“蓝色-红色”这条链设置为备用链。这些节点接纳了新的更长的链,被迫改变了原有对区块链的观点,这就叫做链的重新共识。因为“红”区块做为父区块已经不在最长链上,导致了他们的候选区块已经成为了“孤块”,所以现在任何原本想要在“蓝色-红色”链上延长区块链的矿工都会停下来。全网将“蓝色-绿色-粉色”这条链识别为主链,“粉色”区块为这条链的最后一个区块。全部矿工立刻将他们产生的候选区块的父区块切换为“粉色”,来延长“蓝色-绿色-粉色”这条链。
以上称之为区块链的共识算法。
交易
在比特币体系中,并没有“余额”的概念,所谓某某人的余额是100.00 CNY,意味着的是整个系统中A可以解锁使用的“钱”的总和是100.00 CNY。一次交易的过程,如:A花费10CNY给B购买1杯咖啡,B给A找零2.00 CNY,实际上是指:A解锁10.00 CNY的“钱”,系统“销毁”该笔资金,并生成8.00 CNY只有B能解锁的新钱,以及2.00 CNY只有A能解锁的新钱。从宏观上看,A的账户消费了10.00 CNY的余额并收到2.00 CNY的找零;同时,B的账户增加了8.00 CNY的余额。
锁定和解锁脚本
比特币源自于加密货币,因此涉及了大量密码学的知识,除了上述提到的哈希函数,还使用了非对称密码学的概念:
| 名词 | 可公开性 | 用途 |
|---|---|---|
| Private Key | 不可公开 | 生成数字签名 |
| Public Key | 可公开 | 校验数字签名 |
| Public Key Hash | 可公开 | 收款和解锁 |
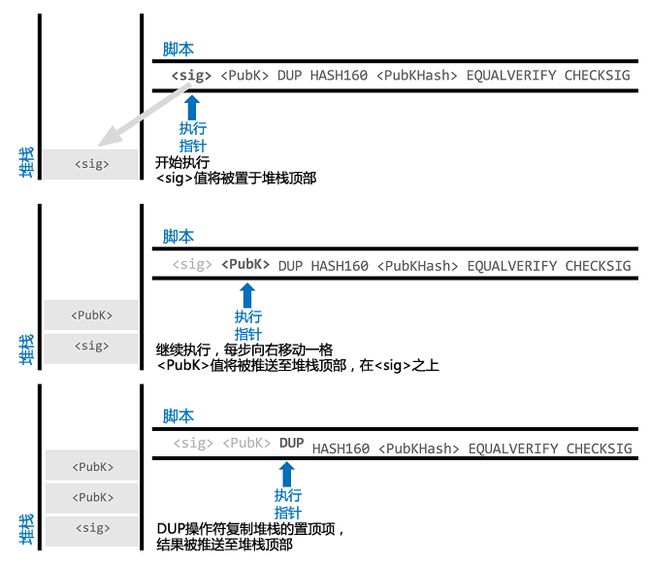
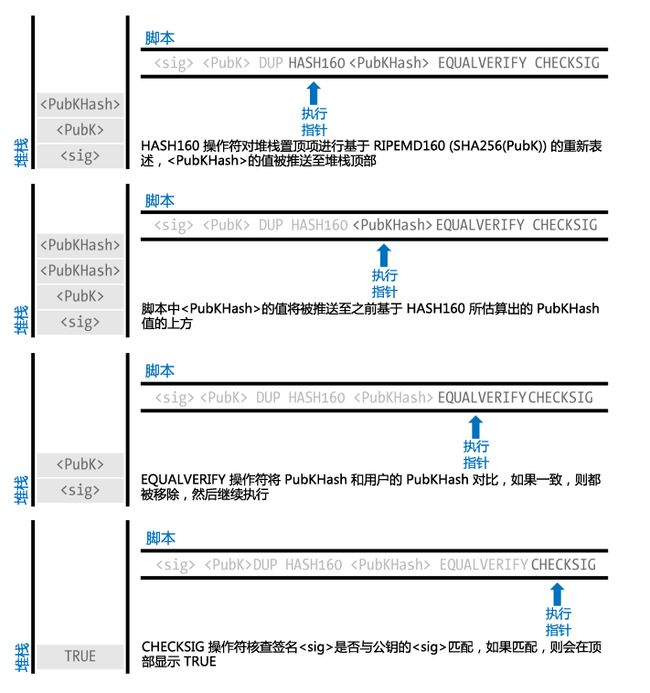
所以,为什么只有A能解锁?
只有通过A提供的
PubK做
Hash160才能得到
PubKHash,才能解开脚本的前半部分,之后再通过
sig和
PubK校验该签名是否合法,并以此判断是否是A主动发起的操作。完整的校验过程如下:
[8]
上述步骤在有些地方也被推广定义为“智能合约”。
匿名性
通过上述的步骤,可以看到私钥由某个用户妥善保存,用于收款的地址通过私钥推导出公钥再经过Hash160得到,因此在网络上,收款人是完全匿名的。
再论Double-Spending
通常说区块链是不可修改的,然而区块链真的是不可修改的么?从以上的介绍可以看到,只要区块的Hash值满足父区块的要求,即被认可为合法区块,而合法区块的最多工作量证明(最长合法区块链)即为区块链的主链,被记录在主链上的交易被认为是不可篡改的。试想一下,如果某个组织占有了全网51%的算力,当ta向你支付价值22亿刀的比特币,你等待了若干个区块后确认收到钱并支付了一架F22战机,这时候组织阴险的嘴脸开始显露,ta启动了超越全网50%算力的矿机,并从你的交易所在的那个区块开始重建一条更长的区块链,并将你从交易的收款人中剔除并更换为另一个人。只要算的够快,很容易出现软分叉,并且最终原本正常的区块被恶意替代。
因此一般的大额交易需要“得到6个区块确认后”才能说安全,如果是巨额的交易需要等待12个以上区块,大约就是2个小时时间。
或许你觉得控制全网51%的算力是一件不可思议的事情,但事实上,比特币并没有按照白皮书所设计的那样通过每个单独的小矿工均参与的模式来生成区块,而是演变为若干小矿工集合形成大矿池模式,并通过leader分配任务,矿工间并行计算,以矿池为单位和其它矿工竞争。可以预见的是,后续矿池还会继续合并,而最终演变为若干巨鳄间的游戏,这不是技术问题,而是经济问题。一旦全网从无数个节点变为若干个巨大矿池很容易出现的问题就是,一些矿池间形成联盟从而掌握50%以上算力。
即使在过去,也曾出现过中国矿池超越全网算力50%以上的事实。更别说那些山寨共有链体系下全网算力或许还不如一台超算的情况。
POW的问题
POW是比特币采用的共识算法,其中一个最主要的问题是,计算无意义的哈希值会导致资源(电能)的大量浪费。
与此同时,比特币网络对于工作量的要求为__平均__10分钟产生下一个区块,这一限制使得整个网络的总体性能急剧下降。区块需要包含这10分钟所有的交易记录,当前比特币区块的限制是1M,平均1笔交易的大小是0.25K,那么当前的极限交易量是:1*1024K/0.25K/Tx/600s大约7Tx/s,同期支付宝的交易承载峰值是100000Tx/s。
或许可以通过降低2个区块产生的间隔来解决问题,但实际上一节已经提到一般交易需要6个区块确认,更准确的说法是:需要记录在区块链的某个区块中,并且此区块后面至少链接了5个区块,总体来说就是60分钟。如果每个区块的生产速度是1分钟,那么攻击的难度也就相对降低了,为了保证交易不会被51%的算力篡改,依然还需要等待大约60分钟。
那么是否可以通过增加区块的大小来增加性能?事实上一个巨大的区块在网络上有效传播对于带宽等硬件设施的要求是极高的。纵使忽略这些客观因素,要提供一个对于当前系统完全无影响,又能同时修改全网上千万个矿工的系统参数的方案几乎也是不可行的。
未完
以上对于区块链的介绍绝大部分是按照比特币的架构进行叙述的,主要包括交易的模型和系统的共识算法两个部分。
很多时候如果读了原版的白皮书,或许会发现很多概念炒的所谓的去中心化的、不可篡改的、分布式账本,更像是S. Haber和W.S. Stornetta在1991年发表的《How to Time-Stamp a Digital Document》[5]中的形态,也就是白皮书所列参考文献中的第三篇。只是论文中加盖时间戳的是数字文档,在比特币中加盖时间戳的是区块本身,而链式的哈希和分布式的时间戳生成模式都在文献中有所提及。
因此,很难说我们口口声声所说的区块链的概念,仅仅是“区块+链”,至少在比特币体系下还包括了一套完整的挖矿机制、奖励机制等等,从技术的角度来说,我觉得只有这一系列完整的合集才是System(抱歉在白皮书里,没有找到BlockChain这个单词)。
然而一系列的高大上的概念,包括私有链、联盟链、区块链1.0,2.0,3.0,大数据,量子,智能已经一股脑的席卷而来,让人在这个浮躁的时代下很快就迷失了,以至于区块链到底是什么,太多时候只是你抄我我抄你的概念。既然没能力给区块链下定义,索性就将之前所学所想整理出来,至于定论,相信每个人都有自己的看法。
不管是不是愿意承认,有太多应用既然打着区块链的名号,不管是不是炒作的概念,不管本身的实现和最初的区块链有多么的不同,既然已经存在,都值得一个技术人员从底层技术的角度去研究、分析,尤其是分布式系统的共识算法,即使抛开其他层面的因素,也是一个技术人员需要攀登的高峰。希望在将来的某一天,对于区块链的认知,可以达到一个新的高度。
如果你看到这里,如果你对阿里感兴趣,请联系我:[email protected]