亲们早安、午安、晚安,上一篇主成分分析法(PCA)等降维(dimensionality reduction)算法-Python主要是了解了PCA的原理和基于Python的基本算法实现,本文主要是学习scikit-learn (sklearn)中关于降维(dimensionality reduction)的一些模型,侧重于PCA在sklearn中的实现。
在sklearn中的Dimensionality Reduction中,包含的降低特征维度的方法包括主成分分析法PCA(这里面又包括不同类型的PCA方法,一般的PCA,KernelPCA, SparsePCA, TruncatedSVD, IncrementalPCA )、因子分析法FA(factor analysis)、独立成分分析ICA等
1、主成分分析法PCA
1)Exact PCA
这个方法主要是利用上一篇主成分分析法(PCA)等降维(dimensionality reduction)算法-Python中的方法,基于奇异值分解(Singular Value Decomposition)来线性降维到低维度的空间。
啥?怎么跑出来个奇异值分解SVD?这是线性代数里的名词,关于线性代数的知识,推荐查看网易公开课里的麻省理工线性代数课程,里面有关于SVD的详细计算。当然,如果想知道SVD的几何意义,我觉得We Recommend a Singular Value Decomposition非常好,图文并茂,极力推荐,由此也进一步理解了主成分分析PCA。
(1)SVD
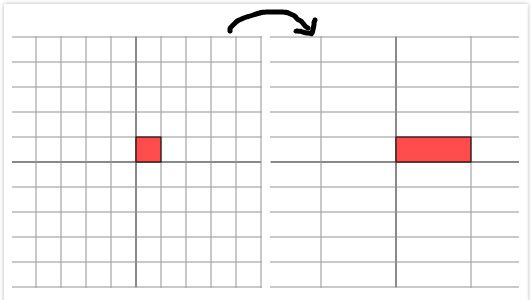
首先考虑对角矩阵如M,如果M与一个向量(x,y)相乘如图1,表示将(x,y)进行长度的变化如图2:
根据图2的变化可知,对角矩阵M的作用是将水平垂直网格作水平拉伸(或者反射后水平拉伸)的线性变化。
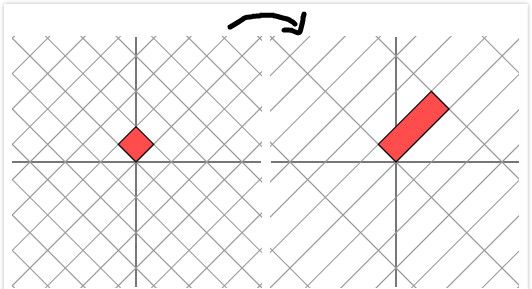
如果M是图3中的对称矩阵,那么它和向量(x,y)相乘后,也可以找到一组网格线(如图4)
看着图4有点蒙圈,貌似不是简单的线性变化,辣么,先把图4中左边图旋转45度,然后再乘以M,然后得到下面的情况:
图5表明,先旋转45度,然后再和M相乘,此时又可以只进行简单的拉伸变化。
对比图4-5,当原始矩阵乘以对称矩阵时,不一定还是进行线性变化(只在一个方向进行伸缩变化),除非这个映射时,两边的正交网络是一致的。
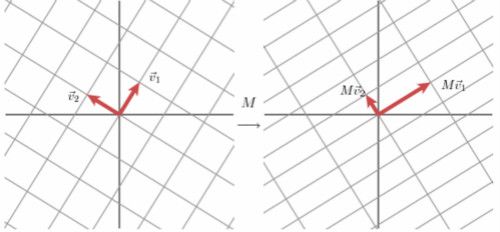
再比如更加一般的非对称非对角矩阵M(如图6):
观察图7,对于任意一个向量,当一个一般矩阵M作用在其上面时,很难只是做线性变化。但是,我们可以如图7最下面一行的变化,找一组网格,找两个正交向量来表示向量。
对角矩阵Σ对角线上的取值σ_1,σ_2就是矩阵M的奇异值。
综上所述:奇异值分解SVD几何意义:对于任何的一个矩阵,我们要找到一组两两正交单位向量序列,是的矩阵作用在此向量序列后得到新的向量序列保持两两正交。奇异值的几何意义:这组变化后的新的向量序列的长度。从图10中看到,奇异值分解和特征值求解很相似,但是特征值必须是方阵才存在,但任何矩阵都可以进行奇异值分解。
好啦,奇异值分解SVD差不多搞清楚了,为啥要进行奇异值分解,其实它表现的就像PCA的意义那样,用这些关键较少数量的奇异值(奇异向量)来表示原来可能比较庞大的东东,因此,在图像压缩等方向应用的比较多。如下:
比如,图11是一个15*25的图片,其像素组成是图12中的M矩阵
结果计算发现,图12中M的非零奇异值只有三个:σ1= 14.72;σ2= 5.22;σ3= 3.31
那么,根据上面奇异值几何意义,其实图11中的图片是可以用这三个奇异值向量来表示的:M=u1σ1v1^T+u2σ2v2^T+u3σ3v3^T,,这一将原来可能要对375个像素点的计算变为123个像素点的计算。还有个问题需要强调,可能实际图片不像图11中那样纯粹,可能存在噪声,如图13(图中出现的那些灰色的地方表示噪声)
图13中像素矩阵得到的奇异值为:σ1= 14.15;σ2= 4.67;σ3= 3.00;σ4= 0.21;σ5= 0.19...
σ15= 0.05等,但是看到还是前三个特征值比较大,因此,继续用σ1,σ2,σ3表示该图片,其他的奇异值舍去,最终得到新的图片见图14,显然图14中噪声变少了。
关于SVD的这个奇异的理解(同时包含PCA于SVD的联系),下面知乎大牛的解释可能更清楚点:
(2)简单PCA模型
class sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', random_state=None)
n_components->表示最终要保留的主成分特征数,如果不设置,则保留全部特征
whiten->是否进行白化,默认为false。啥是白化?因为我们在PCA中,保留主要的特征来计算决策,因此难免有误差,为了降低误差,通过白化来降低特征值之间的相关性,使其协方差矩阵变为对角矩阵。具体,来自知乎大牛关于PCA白化的解释很详细,请参考下图17:
在PCA中,原始数据如图17最左边的红色图表示;然后用原始矩阵减去均值,然后求解协方差矩阵,将数据依据协方差矩阵方差最大的轴进行旋转,得到图17中部绿色显示内容;然后进行白化whiten,就是白化操作的输入是特征基准上的数据,然后对每个维度除以其特征值来对数值范围进行归一化。如果数据服从多变量的高斯分布,那么经过白化后,数据的分布将会是一个均值为零,且协方差相等的矩阵(及单位协方差矩阵),如图17中最右边蓝色图示。
svd_solver->指定奇异值分解SVD的方法,由于特征分解是奇异值分解SVD的一个特例,一般的PCA库都是基于SVD实现的。有4个可以选择的值:{‘auto’, ‘full’, ‘arpack’, ‘randomized’}。randomized一般适用于数据量大(数据量超过500*500),数据维度多同时主成分比例又较低(低于80%)的PCA降维,它使用了一些加快SVD的随机算法。 full则是传统意义上的SVD,使用了scipy库对应的实现。arpack和randomized的适用场景类似,区别是randomized使用的是scikit-learn自己的SVD实现,而arpack直接使用了scipy库的sparse SVD实现。默认是auto,即PCA类会自己去在前面讲到的三种算法里面去权衡,选择一个合适的SVD算法来降维。一般来说,使用默认值就够了。
举栗子1:
篇幅有限(其实是能力+精力有限,捂脸),sklearn中的PCA模型先介绍到这里,以后再深入研究。希望内容对大家有所帮助,也希望大牛不吝赐教。