自动上色论文《Learning Diverse Image Colorization》

Abstract
作者指出，着色问题是ill-posed以及模棱两可的，是典型的多模态问题。过去的着色问题往往只考虑其最有可能的着色方案；而作者希望通过这篇论文对着色问题的本质建模，并生成具有空间连贯性(long-scale spatial co-ordination)的着色结果。作者通过变分自编码器（VAE）学习色域的低维度的embedding，并设计损失函数来避免模糊的输出结果，以及考虑到像素颜色的不均匀分布。最后，作者为灰度图像和色域的低维度嵌入之间的多模态分布建立了条件模型。验证表示，此模型效果优于传统的条件变分自编码模型，以及较有名的cGAN模型。
Introduction
上色问题要求较高，因为需要考虑局部特征以及大尺度的空间特征。由于只考虑局部特征会导致生成的结果图片失去耦合性，因此需要考虑一种既考虑对每个像素的估计(per-pixel color estimates)，又考虑空间连贯性的方法。这种方式对于需要多个预测的许多模糊的视觉任务是常见的,即：从静态图像[1]生成运动场，合成未来帧[2]，延时视频[3]，交互式分割和姿势估计[4]等。

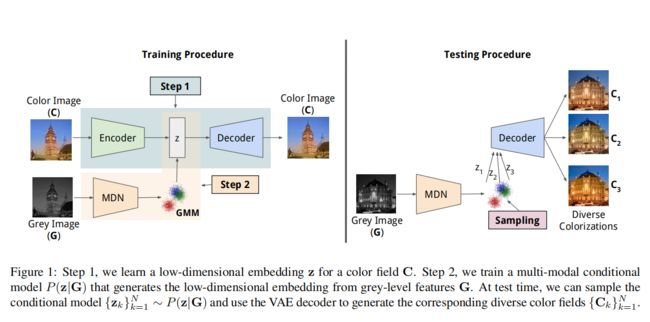
一个解决方法是使用条件模型P(C|G),C是图片的色域，G是灰度图片。可以在条件模型上画一些样本点$\{C_k{\}}_{k=1}^N$从而获得多样的着色结果。然而，这种详细的条件模型设计起来很难，因为C和G在高维空间中离散分布。因此作者使用了降维的思想，使用VAE（变分自编码器），将色域C用他的低维度的嵌入结果z来表示；之后使用混合密度网络(MDN)学习多模态条件模型P(z|G)。灰度图G的特征由一个着色卷积神经网络[5]的7层卷积结果生成。这些特征将空间结构与逐像素的特征编码。最后在测试阶段，作者使用多个样本$\{z_k{\}}_{k=1}^{N}P(z|G)$,并使用VAE解码器获得对应的着色结果$C_k$。本文通过对色域的空间结构进行编码，并通过在条件模型上采样获得空间相关的多样化着色。

贡献如下：
1、作者通过学习平滑的低维嵌入（Embedding）以生成具有高保真度的相应色域。
2、通过在灰度图特征和低维嵌入之间学习多模态条件模型，从而生成多样性的着色。
3、本方法在着色问题上可超过CVAE和cGAN。
对色域的编码与解码
本文通过VAE（变分自编码器）来进行色域嵌入：除此之外，本文也使用了一种有效的解码器从而从给定的Embedding中生成真实化的色域。本文不使用常见的L2误差，因为它会带来过度平滑或褪色的色域。
解码器损失
特异性
top-k主成分$P_k$是在色域的高度差异空间中具有最大方差的投影的方向。因此，产生主要沿着top-k主成分变化的色域，以生成的色域中的特异性为代价来减少L2损失。为了避免这一点，本文沿着top-k主成分投影生成的色域$f(z,\theta )$和Ground Truth色域C。本文使用k = 20。接下来，作者将沿着每个主成分的这些投影之间的差除以从训练集中估计的相应标准偏差${\sigma }_k$。这鼓励所有主要组成部分的变化在本文的损失中处于平等地位。将残差除以第k个（对于本文的情况为第20个）组分的标​​准偏差。使用这些距离和残差的平方和可以写出特异性损失${\mathcal{L}}_{mah}$
$${\mathcal{L}}_{mah}=\sum _{k=1}^{20}\frac{||[C-f(z,\theta {)}^T{P}_k|{|}_2^2}{{\sigma }_k^2}+\frac{||C_{res}-f_{res}(z,\theta )|{|}_2^2}{{\sigma }_{20}^2}$$
$$C_{res}=C-\sum _{k=1}^{20}{C}^T{P}_k{P}_k$$
$$f_{res}(z,\theta )=f(z,\theta )-\sum _{k=1}^{20}f(z,\theta {)}^T{P}_k{P}_k$$
上述损失使用马氏距离。
着色性
本文使用经验概率估计(或归一化直方图)H的颜色在量化的“ab”色域的计算。对于像素p，本文对其进行量化去获得其bin并检索$\frac{1}{H_p}$的逆矩阵。$\frac{1}{H_p}$被用于在预测的颜色$f_p(z,\theta )$与Ground Truth $C_p$之间进行平方项的预测。本文可以写出这个损失函数${\mathcal{L}}_{hist}$
$${\mathcal{L}}_{hist}=||(H^{-1}{)}^T[C-f(z,\theta )]|{|}_2^2$$
梯度
本文还使用第一个损失项，鼓励生成的色域具有与Ground Truth相同的梯度。将水平和垂直梯度算子写做$\nabla h$和$\nabla v$。梯度的loss为：$${\mathcal{L}}_{grad}=||{\nabla }_{h}C-{\nabla }_{h}f(z,\theta )|{|}_2^2+||{\nabla }_{v}C-{\nabla }_{v}f(z,\theta )|{|}_2^2$$
解码器整体的损失函数为$${\mathcal{L}}_{dec}={\mathcal{L}}_{hist}+{\lambda }_{mah}{\mathcal{L}}_{mah}+{\lambda }_{grad}{\mathcal{L}}_{grad}$$
这里设置超参数${\lambda }_{mah}=0.1$以及${\lambda }_{grad}=10^{-3}$
编码器的损失函数用KL散度表示。
相对于解码器的损失函数，本文将该损失函数加权$10^{-2}$倍。这放松了对低维嵌入的正则化，但是对解码器产生的色域的保真度给出了更大的提高。本文对嵌入空间的宽松约束并没有产生不利影响。因为本文的条件模型（参考第4节）设法产生解码为自然色彩的低维嵌入。
条件模型(灰度图G到低维嵌入z)
混合密度网络(MDN)对目标向量的条件概率分布进行建模，将高斯混合作为输入。这将考虑一对多的映射并允许目标向量使用多个基于同一个输入值的结果来显示出最终的多样性。
MDN损失本文使用MDN函数来进行条件概率分布的建模。$P(z|G)$是一个有M个组成部分的高斯混合模型。损失函数在对数域中将该模型函数最小化。${\mathcal{L}}_{mdn}$作为MDN损失函数，${\pi }_i$代表混合结果的系数，${\mu }_i$作为其平均值，$\sigma$代表对于GMM的固定球面协方差。MDN损失函数如下：
$${\mathcal{L}}_{mdn}=-log(P(z|G))=-log\sum _{i=1}^M{\pi }_i(G,\varphi )\mathcal{N}(z|{\mu }_i(G,\varphi ),\sigma )$$
对loss进行优化的难度很大，因为其包括了对指数化的$e^{-\frac{-||z-{\mu }_i(G,\varphi )|{|}_2^2}{2{\sigma }^2}}$的加和的取对数。当网络训练开始的时候，$||z-{\mu }_i(G,\varphi )|{|}_2$很高，会导致在指数计算中出现数值下溢。为了避免数值下溢，本文选择高斯分量$m=argmi{n}_i||z-{\mu }_i(G,\varphi )|{|}_2$来预测平均值最接近基准值的z，并且每个训练步骤仅优化该部分。损失函数从而用如下方式表示：
$${\mathcal{L}}_{mdn}=-log{\pi }_m(G,\varphi )+\frac{||z-{\mu }_m(G,\varphi )|{|}_2^2}{2{\sigma }^2}$$
直观地，这种最小近似解决了MDN网络的可识别性（或对称性）的问题，因为我们将灰度级特征与上述的部分（比如第m个组件）联系起来。其他部分可通过附近的灰度特征进行自由优化。本文之后证明，这种基于MDN的策略比CVAE和cGAN可以产生更好的多样化着色结果。
VAE的架构：

MDN的输入是来自[30]的灰度级特征G，并且具有28×28×512的维度。我们在MDN的输出GMM中使用8个组件(component)。输出层包括用于平均数的8×d激活层和用于8个组件的混合权重的8次Softmax激活函数。我们使用0.1的固定球面方差。 MDN网络使用5个卷积层，然后是两个全连接层，可以写成：Input(28×28×512)→CReLU（5,1,384）→B→CReLU（5,1,320）→B→CReLU （5,1,288）→B→CReLU（5,2,256）→B→CReLU（5,1,128）→B→FC（4096）→FC（8×d + 8）。
同样，MDN是一个具有12个卷积层和2个全连接层的网络，前7个卷积层在[30]的任务上进行了预训练并保持固定。
在测试时，我们可以从MDN中采样多个嵌入，然后使用VAE解码器生成各种颜色。然而，为了以主成分分析的方式研究不同的着色，我们采用不同的过程。我们按照混合权重${\pi }_i$的降序对预测均值${\mu }_i$进行排序，并使用这些top-k（k = 5）均值作为下图所示的不同颜色。

[1]J. Walker, C. Doersch, A. Gupta, and M. Hebert. An uncertain future: Forecasting from static images using variational autoencoders. In European Conference on Computer Vision, 2016. 1, 4
[2]T. Xue, J. Wu, K. L. Bouman, and W. T. Freeman. Visual dynamics: Probabilistic future frame synthesis via cross convolutional networks. In NIPS, 2016. 1, 4
[3]Y. Zhou and T. L. Berg. Learning Temporal Transformations from Time-Lapse Videos, pages 262–277. Springer International Publishing, 2016. 1, 4
[4] D. Batra, P. Yadollahpour, A. Guzmn-Rivera, and G. Shakhnarovich. Diverse m-best solutions in markov random fields. In ECCV (5), volume 7576 of Lecture Notes in Computer Science, pages 1–16. Springer, 2012. 1
[5]R. Zhang, P. Isola, and A. A. Efros. Colorful image colorization. ECCV, 2016. 1, 2, 3, 5