论文阅读笔记:目标追踪结合相关滤波器资料收集!
| 目标追踪结合相关滤波器资料收集! |
文章目录
- 一、目标追踪结合相关滤波器资料收集!
- 1.1. 参考文章
- 1.2. Visual Object Tracking using Adaptive Correlation Filters(MOSSE)
- 1.3. 相关滤波器用于跟踪的原理
- 1.4. High-Speed Tracking with Kernelized Correlation Filters(KCF)
- 1.4.1. 总体思路
- 1.4.2. 输入帧检测
- 1.4.3. 总结
- 二、补充:机器学习和深度学习基础补充:
- 2.1. 训练集测试集划分以及验证方法
- 2.1.1. 留出法
- 2.1.2. K折交叉验证
- 2.1.3. 分层抽样策略(Stratified k‐fold)
- 2.1.4. 用网格搜索来调超参数(论文调参大多是这种方法!)
- 2.2. 向量范数矩阵范数
- 2.2.1. 向量范数
- 2.2.2. 矩阵范数
一、目标追踪结合相关滤波器资料收集!
1.1. 参考文章
主要参考下面的作者文章,在这里表示感谢!
- 总结:相关滤波器(Correlation Filters)
- 循环矩阵傅里叶对角化
- 目标跟踪: 相关滤波器 循环矩阵
- 目标跟踪之相关滤波
- 核化相关滤波器高速跟踪:KCF(2015PAMI)
1.2. Visual Object Tracking using Adaptive Correlation Filters(MOSSE)
- 摘自作者:目标跟踪之相关滤波 和 总结: 相关滤波器(Correlation Filters)
- 对于一张图像来讲,问题描述为要找到一个 滤波模版 h h h,与输入图像 f f f 求相关性,得到响应输出 g g g。同时 为了方便理解,用一幅图来进行说明(相关图 g g g 描述目标响应,越接近时值越大):
g = f ⊗ h g=f \otimes h g=f⊗h
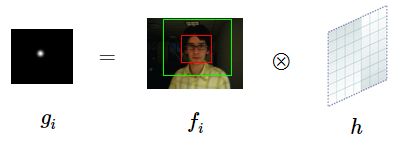
-
其中符号 ⊗ \otimes ⊗ 表示卷积计算,在计算机中运算开销很大,因此这里作者引入傅里叶变换(FFT), 这样卷积操作经过FFT操作操作之后变成了点乘操作,极大减少了运算的开销。
F ( g ) = F ( f ⊗ h ) = F ( f ) ⋅ F ( h ) ∗ F(g)=F(f \otimes h)=F(f) \cdot F(h)^{*} F(g)=F(f⊗h)=F(f)⋅F(h)∗ -
通过上面的公式,将复杂的互相关(卷积)计算转换成点乘。注意后面的 F ( h ) ∗ F(h)^{*} F(h)∗ 是共轭,与卷积不同上面的公式可以简化描述为:
G = F ⋅ H ∗ {G=F \cdot H^{*}} G=F⋅H∗ -
有了上面的公式,那么后面的任务就是找到 H ∗ H^{*} H∗(滤波模板):
H ∗ = G F {H^{*}=\frac{G}{F}} H∗=FG -
但是实际情况中,我们要考虑目标的外观变换等因素影响,所以我们同时考虑目标的 m m m 个图像作为参考,从而提高滤波模板的鲁棒性,MOSSE 提出的方法就是最小化平方和误差,也就是针对 m m m 个样本求最小二乘,描述为:
min H ∗ = ∑ i = 1 m ∣ H ∗ F i − G i ∣ 2 \min _{H^{*}}=\sum_{i=1}^{m}\left|H^{*} F_{i}-G_{i}\right|^{2} H∗min=i=1∑m∣H∗Fi−Gi∣2 -
因为上述公式的操作都是元素级别的,因此要找到 m i n min min,将图像展开到像素,每个像素是独立计算的 ( w w w 和 v v v 是 H H H 中每个元素的索引!),因此我们有如下:
min H w v ∗ ∑ i = 1 m ∣ H w v ∗ F w v i − G w v i ∣ 2 \min _{H_{w v}^{*}} \sum_{i=1}^{m}\left|H_{w v}^{*} F_{w v i}-G_{w v i}\right|^{2} Hwv∗mini=1∑m∣Hwv∗Fwvi−Gwvi∣2 -
想要得到最小的 H w v ∗ H_{w v}^{*} Hwv∗,只需要对上式求偏导 = 0 =0 =0,即是:
0 = ∂ ∂ H w v ∗ ∑ i ∣ F i w v H w v ∗ − G i w v ∣ 2 0=\frac{\partial}{\partial H_{w v}^{*}} \sum_{i}\left|F_{i w v} H_{w v}^{*}-G_{i w v}\right|^{2} 0=∂Hwv∗∂i∑∣FiwvHwv∗−Giwv∣2 0 = ∂ ∂ H w v ∗ ∑ i ( F i w v H w v ∗ − G i w v ) ( F i w v H w v ∗ − G i w v ) ∗ 0=\frac{\partial}{\partial H_{w v}^{*}} \sum_{i}\left(F_{i w v} H_{w v}^{*}-G_{i w v}\right)\left(F_{i w v} H_{w v}^{*}-G_{i w v}\right)^{*} 0=∂Hwv∗∂i∑(FiwvHwv∗−Giwv)(FiwvHwv∗−Giwv)∗ 0 = ∂ ∂ H w v ∗ ∑ [ ( F i w v H w v ∗ ) ( F i w v H w v ∗ ) ∗ − ( F i w v H w v ∗ ) G i w v ∗ − G i w v ( F i w v H w v ∗ ) ∗ + G i w v G i w v ∗ ] 0=\frac{\partial}{\partial H_{w v}^{*}} \sum\left[\left(F_{i w v} H_{w v}^{*}\right)\left(F_{i w v} H_{w v}^{*}\right)^{*}-\left(F_{i w v} H_{w v}^{*}\right) G_{i w v}^{*}-G_{i w v}\left(F_{i w v} H_{w v}^{*}\right)^{*}+G_{i w v} G_{i w v}^{*}\right] 0=∂Hwv∗∂∑[(FiwvHwv∗)(FiwvHwv∗)∗−(FiwvHwv∗)Giwv∗−Giwv(FiwvHwv∗)∗+GiwvGiwv∗] 0 = ∂ ∂ H w v ∗ ∑ i F i w v F i w v ∗ H w v H w v ∗ − F i w v G i w v ∗ H w v ∗ − F i w v ∗ G i w v H w v + G i w v G i w v ∗ 0=\frac{\partial}{\partial H_{w v}^{*}} \sum_{i} F_{i w v} F_{i w v}^{*} H_{w v} H_{w v}^{*}-F_{i w v} G_{i w v}^{*} H_{w v}^{*}-F_{i w v}^{*} G_{i w v} H_{w v}+G_{i w v} G_{i w v}^{*} 0=∂Hwv∗∂i∑FiwvFiwv∗HwvHwv∗−FiwvGiwv∗Hwv∗−Fiwv∗GiwvHwv+GiwvGiwv∗ 0 = ∑ i [ F i w v F i w v ∗ H w v − F i w v G i w v ∗ ] 0=\sum_{i}\left[F_{i w v} F_{i w v}^{*} H_{w v}-F_{i w v} G_{i w v}^{*}\right] 0=i∑[FiwvFiwv∗Hwv−FiwvGiwv∗] H w v ∗ = ∑ i F i w v G i w v ∗ ∑ i F i w v F i w v ∗ H_{w v}^{*}=\frac{\sum_{i} F_{i w v} G_{i w v}^{*}}{\sum_{i} F_{i w v} F_{i w v}^{*}} Hwv∗=∑iFiwvFiwv∗∑iFiwvGiwv∗
- 上面得到的是 H w v ∗ H_{w v}^{*} Hwv∗ 是 H ∗ H^{*} H∗ 中每个元素的值,最后得到的 H ∗ H^{*} H∗ 为:
H ∗ = ∑ i F i ⋅ G i ∗ ∑ i F i ⋅ F i ∗ H^{*}=\frac{\sum_{i} F_{i} \cdot G_{i}^{*}}{\sum_{i} F_{i} \cdot F_{i}^{*}} H∗=∑iFi⋅Fi∗∑iFi⋅Gi∗
- 但是在跟踪中如何更新滤波器 H ∗ H^{*} H∗呢? F i F_{i} Fi 和 G i G_{i} Gi 又怎么获取呢?在作者的文章中,其对跟踪框 (ground truth) 进行随机变换,获取一系列的样本 F i F_{i} Fi,而 G i G_{i} Gi 是由高斯函数产生,并且其峰值在 F i F_{i} Fi 的中心位置,获取一系列的训练样本和结果之后,就可以计算滤波器 H ∗ H^{*} H∗ 的值 (注意:这里的 F i F_{i} Fi, G i G_{i} Gi, H ∗ H^{*} H∗ 的 s i z e size size 大小都相同! )。
- 作者为了让滤波器对光照,形变有良好的鲁棒性,提出了一个更新算法,根据当前帧不断进行调整,即在线更新策略,调整策略如下:
H i ∗ = A i B i H_{i}^{*}=\frac{A_{i}}{B_{i}} Hi∗=BiAi A i = η G i ⋅ F i ∗ + ( 1 − η ) A i − 1 B i = η F i ⋅ F i ∗ + ( 1 − η ) B i − 1 \begin{array}{l}{A_{i}=\eta G_{i} \cdot F_{i}^{*}+(1-\eta) A_{i-1}} \\\\ {B_{i}=\eta F_{i} \cdot F_{i}^{*}+(1-\eta) B_{i-1}}\end{array} Ai=ηGi⋅Fi∗+(1−η)Ai−1Bi=ηFi⋅Fi∗+(1−η)Bi−1
- 作者将滤波器的模板公式分为分子和分母两部分,每个部分都分别进行更新,其中 η η η 为学习率,一般设置为 0.1 0.1 0.1, A i A_{i} Ai 和 A i − 1 A_{i-1} Ai−1当前帧和上一帧的分子。
1.3. 相关滤波器用于跟踪的原理
-
对于输入的第一帧图像,将给定的要追踪的区域提取出特征,然后进行训练,得到相关滤波器。
-
对于之后的每一帧,先裁剪下之前预测的区域,然后进行特征提取,这些特征经过 c o s cos cos 窗函数之后,做 FFT 变换,然后与相关滤波器相乘,将结果做 IFFT 之后,最大响应点所在的区域即为要追踪目标的新位置,然后再用新位置区域训练更新得到新的相关滤波器,用于之后的预测。
-
目前跟踪算法主流的思想还是基于 tracking by detection,而 训练样本的选择基本上就以目标中心提取正样本,然后基于周围的图像提取负样本。 大多数算法采用非正即负的方法来标记训练样本,即正样本标记为 1 1 1,负样本标记为 0 0 0。但是,这种标记样本的方法不能很好反映每个负样本的权重。即对离中心目标远的样本和离中心目标近的样本被同等对待。 于是,有的算法提出了使用连续的标签标记样本,即根据样本中心离目标的远近分别赋值 [ 0 − 1 ] [0-1] [0−1] 范围的数。离目标越近,值越趋向于 1 1 1,离目标越远,值越趋向于 0 0 0。比如stuk和KCF用这种方法标记样本取得了较好的效果。
-
struck是通过一种 loss函数 隐式地采用了这种连续的样本标记方法。KCF是一种 鉴别式追踪方法,这类方法一般都是在追踪过程中训练一个目标检测器,使用目标检测器去检测下一帧顸测位置是否是目标,然后再使用新检测结果去更新训练集进而更新目标检测器。而在训练目标检测器时一般选取目标区域为正样本,目标的周围区域为负样本,当然越靠近目标的区域为正样本的可能性越大。KCF通过使用 [ 0 − 1 ] [0-1] [0−1] 范围的值作为样本的回归值,从而给不同偏移下得到的样本不同的权重。
-
相对于其他方法每次在前一帧的bb周围密集采样,每一帧都要计算上一帧 b b bb bb 周围的很多样本的 f e a t u r e feature feature,比较耗时,但如果放弃密集采样而是随机少取一些样本进行训练的话,效果又不如密集时好。怎样才能仍然坚持密集采样,但又提高计算性能呢?KCF考虑由目标 b b bb bb 的 w i n d o w window window 循环移位 构建出了训练样本,而不是随机选取周围样本。因为循环矩阵的特殊性,把问题的求解变换到了离散傅里叶域,从而避免了矩阵求逆的过程,再借助于FFT变换,将卷积变换为频域的 dot-product, 大大降低了计算的复杂度, 提高了处理速度。
1.4. High-Speed Tracking with Kernelized Correlation Filters(KCF)
- 这篇论文是近年来跟踪界最经典的论文,没有之一。主要思想就是利用了循环矩阵对角化等性质,使得核化之后的计算变得十分简单。原理很复杂,代码很简单。
- 摘自作者:核化相关滤波器高速跟踪:KCF(2015PAMI)
1.4.1. 总体思路
- 所谓的相关滤波方法就是根据当前帧的信息和之前帧的信息训练出一个相关滤波器,然后与新输入的帧进行相关性计算,得到的置信图就是预测的跟踪结果,显然,得分最高的那个点(或者块)就是最可能的跟踪结果。
- 由于KCF里并没有任何的流程图,所以我们借助Kaihua Zhang的STC[1]中的配图来理解一下,看着配图应该能理解主要的流程了。这里要说一下,为什么能用其它论文的配图,因为我们介绍的这篇KCF和STC都是对12年CSK的改进,不同的是,KCF是在CSK基础上加了HOG特征使得效果大大提升了,STC是在贝叶斯的框架下对CSK进行解释并在其中加入了上下文 (context) 信息的应用。 所以本质上来说,这几个都是一样的流程。
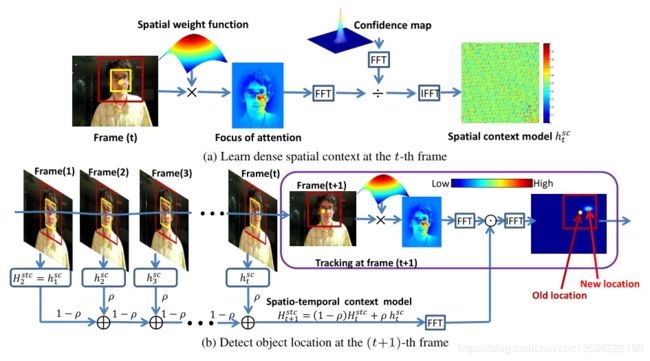
- 上面的部分就是利用之前帧的跟踪结果图片训练出相关滤波器。我们将原始的问题表述为: f ( z ) = w T z f(\mathbf{z})=\mathbf{w}^{T} \mathbf{z} f(z)=wTz
- 优化函数由凸优化里最简单的最小二乘和正则项组成,也就是最常用的岭回归方法: min w ∑ i ( f ( x i ) − y i ) 2 + λ ∥ w ∥ 2 \min _{\mathbf{w}} \sum_{i}\left(f\left(\mathbf{x}_{i}\right)-y_{i}\right)^{2}+\lambda\|\mathbf{w}\|^{2} wmini∑(f(xi)−yi)2+λ∥w∥2
- 这里的理想回归期望(标签)假设是高斯型,直观上理解就是离上一帧跟踪结果越近,那么它是这一帧的跟踪结果的概率也就越大。如下图,下一帧中心点的位置在黄色点周围的可能性大,不会跑太远,所以理想回归函数也就是中间大周围小。

- 因为最小二乘类的优化方法已经很成熟了,所以我们可以直接用公式求解(其实就是求偏导令其等于0): w = ( X T X + λ I ) − 1 X T y \mathbf{w}=\left(X^{T} X+\lambda I\right)^{-1} X^{T} \mathbf{y} w=(XTX+λI)−1XTy
- 看起来比较复杂,又是共轭转置又是求逆的,所以要简化一下。那么本文也是常规思路,把非线性问题转化为线性问题,所以就想到了SVM中也用到的核技巧(注意我们这里推导的时候用的是点积核,但其实核函数还有多项式核、径向基核及高斯核等),引入核函数后能够把参数训练问题简化: α = ( K + λ I ) − 1 y \boldsymbol{\alpha}=(K+\lambda I)^{-1} \mathbf{y} α=(K+λI)−1y
- 这里的 K K K 是两个矩阵的核相关性。看起来似乎已经简化了很多了,但是,还是有求逆!求逆杀伤力太强了,不行,一定还要简化。怎么办呢?这时循环矩阵对角化的性质派上用场了,利用循环矩阵的性质,使得训练过程进一步简化。 α ^ = y ^ k ^ x x + λ \hat{\alpha}=\frac{\hat{\mathbf{y}}}{\hat{\mathbf{k}}^{\mathbf{x} \mathbf{x}}+\lambda} α^=k^xx+λy^
- 这里顶上的符号是复域的意思。不管你信不信,反正我是信了,竟然如此简单,这里详细的推导过程放在后面的部分。
1.4.2. 输入帧检测
- 下面的部分就是对新输入的帧进行检测,其实就是跟滤波器计算出相关性再乘上回归系数,如果是新手听不懂没关系,后面会再讲的哦。右下角的置信图(就是各个点是跟踪结果的可能性)用公式来表达就是如下: f ^ ( z ) = k ^ x z ⊙ α ^ \hat{\mathbf{f}}(\mathbf{z})=\hat{\mathbf{k}}^{\mathbf{x z}} \odot \hat{\boldsymbol{\alpha}} f^(z)=k^xz⊙α^
- 没错,就是这么简单就能求出输入帧的跟踪结果了。如上图右下角所示,新的跟踪结果比原跟踪结果往右上方移了一些,直观上来看红色框中David的脸确实往右上方移动了一些,所以结果应该是对的,当然这只是我们肉眼看到的结果,真正结果好不好还要看在数据集上跑的结果,KCF的结果会在之后的实验部分讲,结果是相当好的,当然那是在2014年的时候。

- 那么这里得到的响应矩阵(置信图)该怎么理解呢?便于理解,故放一张图。这里也是循环采样的精髓之处。
 !
!
- 如上图,最后得到的响应矩阵其实可以理解成一种密集的采样对应的响应矩阵,左上角(上图中第1行第1列)的响应值就是预测的当前输入帧以这个点为中心的可能性,当然这个点的预测值肯定是很低的,因为我下一帧很难跑到那里去。以此类推,MxN个响应对应的就是MxN种循环移位。下面一句话是重点,所谓的循环矩阵到这里就大显身手了,仔细想想,第ij块表示原图下移i行右移j列,那么换句话说,好像我所有的这MxN个循环移位的矩阵只要用一个量就可以表示了。
- 有没有一种熟悉的感觉?对,就是基波和谐波。类比一下,我用一个基波和一个倍数就能表示所有的谐波了,这里的原图就是基波,而位移之后的图就是谐波。自然地,既然那么像,那我们就试试傅立叶变换呗,一试就成了,因为需要计算的量很少,所以速度快,因为密集采样样本大大增加,所以跟踪的效果又很好。

- 如果你不是做跟踪这行的话,可能会问,右下角t+1帧的时候为什么红色框的中心(也就是黄色小点)不是David的鼻子那里,那是因为这个红色框是根据上一帧的跟踪结果来画的,这个小黄点的位置其实是上一帧David(David也算是个数据集中的明星0.0)鼻子的位置,这也是常见做法,先用上一帧的结果在当前输入帧框出一个大框,然后跟最新的滤波器做相关性计算,相关性最大的就是鼻子那块,也就是当前输入帧的跟踪结果。
- 其实讲到这里已经把精髓讲完了,下面讲一些推导细节,加深理解。
- 循环矩阵对角化有神奇效果,大大降低了运算量。首先举个例子,来展现它神奇的效果。就拿上文出现的岭回归公式当例子吧,看看能把它简化成什么样。原始公式: w = ( X T X + λ I ) − 1 X T y \mathbf{w}=\left(X^{T} X+\lambda I\right)^{-1} X^{T} \mathbf{y} w=(XTX+λI)−1XTy
- 在复域中(H表示共轭转置)即: w = ( X H X + λ I ) − 1 X H y \mathbf{w}=\left(X^{H} X+\lambda I\right)^{-1} X^{H} \mathbf{y} w=(XHX+λI)−1XHy
- 化简过程:

-
这是我早前推的,比起他的公式,我个人更喜欢他的代码嘻嘻。这个公式推下来并没有用,只是让我们见识一下循环矩阵化简的威力,真正用到代码里去的是下面3个推导。
-
大家是否还记得我们这里实际上用到的是核化的岭回归啊?也就是比普通的稍微简化了一些的,所以推导起来也比较容易。
-
原始公式: α = ( K + λ I ) − 1 y \boldsymbol{\alpha}=(K+\lambda I)^{-1} \mathbf{y} α=(K+λI)−1y
-
化简过程:

- 嗯,好像看起来还不错哦,既没有求逆又没有很多矩阵乘法运算。它的代码其实更感人。

- 检测出跟踪结果,就是当前输入的帧和滤波器求相关性,相关性最大的即为跟踪结果。
- 原始公式: f ( z ) = ( K z ) T α \mathbf{f}(\mathbf{z})=\left(K^{\mathbf{z}}\right)^{T} \boldsymbol{\alpha} f(z)=(Kz)Tα
- 化简过程:

- 嗯,这篇论文真是不断地感动着我们这些吃瓜群众,原来可以这么简单。看着公式,代码闭着眼睛都能编了。

- 现在只剩一个问题了,那就是核相关性怎么求。
- 核相关性的化简。好像解决了这个就完美了,那这个核相关性好求吗?如果不好求的话,就空亏一篑了,放心,跟踪界的allstar Henriques(葡萄牙人的名字我至今不会读)当然已经帮我们解决好了,依然简单。
- 原式公式: k x x ′ k^{x x^{\prime}} kxx′
- 化简过程:
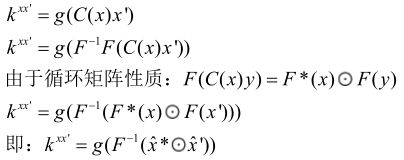
- 我们这里只推导点积核。剩下的多项式核,径向基核,高斯核类比就能得到。论文里效果最好的是高斯核。

- 注意,代码里第2行是使用HOG特征的关键,他把31层HOG特征全部加起来了,这个简单的操作使得之前的CSK能用很多高维特征,故性能大增。
- 实验。我在OTB50上跑了0.514,因为加入了形状特征HOG,所以抗光照等性能骤升,当时(2014年)能排世界第3,由于实现起来非常简单,在很多人眼里是近年来跟踪界当之无愧的最佳论文(其实是在我眼里)。
- 本人跑的结果:
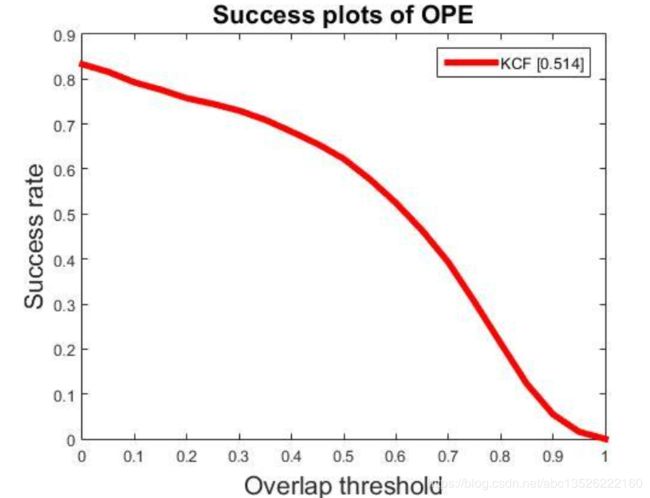
- 作者论文中的对比实验结果:
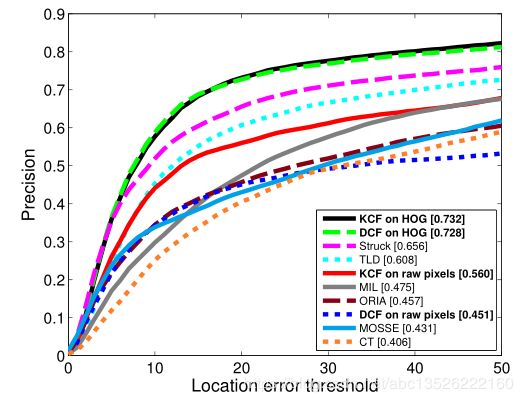
1.4.3. 总结
-
本论文使用了HOG特征+核函数法把相关滤波器领域又推到了一个新的高度上。KCF是原理很复杂,实现很简单的代表作之一。
-
知乎网友王康康解答:
w = ( X H X + λ I ) − 1 X H y \mathbf{w}=\left(X^{H} X+\lambda I\right)^{-1} X^{H} \mathbf{y} w=(XHX+λI)−1XHy ( X H X + λ I ) w = X H y \left(X^{H} X+\lambda I\right) \mathbf{w}= X^{H} \mathbf{y} (XHX+λI)w=XHy -
左边是循环矩阵 ( X H X + λ I ) \left(X^{H} X+\lambda I\right) (XHX+λI) 乘以普通矩阵 w \mathbf{w} w, 等价于循环矩阵的“单个向量”卷积上那个普通矩阵。 { \{ {在这里, X X X 代表了多幅图,假设图像长宽均为 N N N,那么此处 X X X 的维度是 N N N (长) 乘 N N N (宽) 乘 N N N (幅数) } \} }
-
同时呢,我此处所指的“单个向量” 就是【N(长) 乘 N(宽)】了,把它叫做image。此时有
( X H X + λ I ) w = X H y \left(X^{H} X+\lambda I\right) \mathbf{w}= X^{H} \mathbf{y} (XHX+λI)w=XHy 等效于 image卷积 w = X H y \mathbf{w}=X^{H} \mathbf{y} w=XHy,再变道频域便可得出结论。 -
所以总的推导就3步
w = ( X H X + λ I ) − 1 X H y (1) \mathbf{w}=\left(X^{H} X+\lambda I\right)^{-1} X^{H} \mathbf{y} \tag{1} w=(XHX+λI)−1XHy(1) ( X H X + λ I ) w = X H y (2) \left(X^{H} X+\lambda I\right) \mathbf{w}= X^{H} \mathbf{y}\tag{2} (XHX+λI)w=XHy(2) i m a g e 卷 积 w = X H y (3) image卷积 \mathbf{w}=X^{H} \mathbf{y}\tag{3} image卷积w=XHy(3) F ( i m a g e ) . ⋆ F ( w ) = F ( X H y ) (4) F( image ).^{\star} F(\mathrm{w})=\mathrm{F}(X^{H} \mathbf{y})\tag{4} F(image).⋆F(w)=F(XHy)(4) -
参考:KCF公式推导错误及验证
二、补充:机器学习和深度学习基础补充:
2.1. 训练集测试集划分以及验证方法
2.1.1. 留出法

2.1.2. K折交叉验证
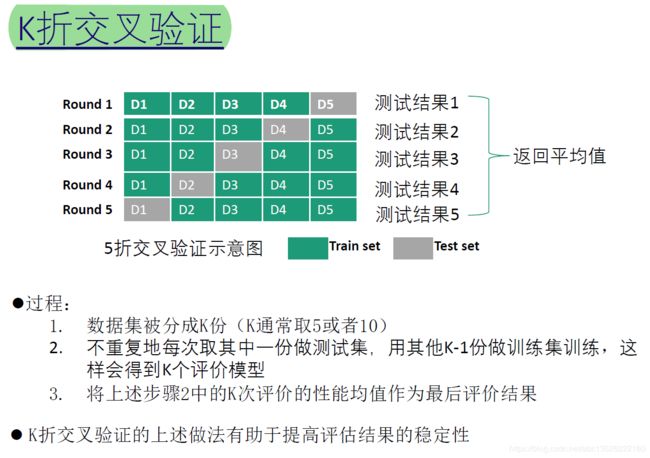
2.1.3. 分层抽样策略(Stratified k‐fold)
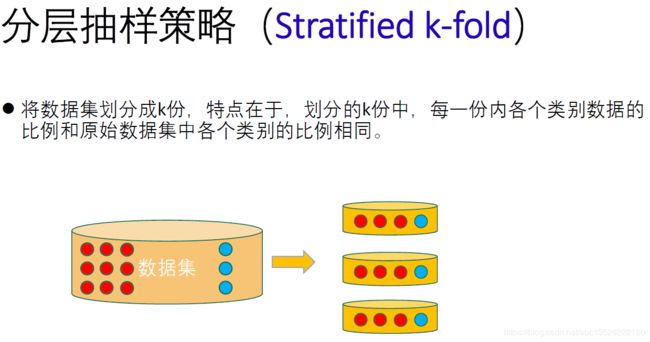
2.1.4. 用网格搜索来调超参数(论文调参大多是这种方法!)
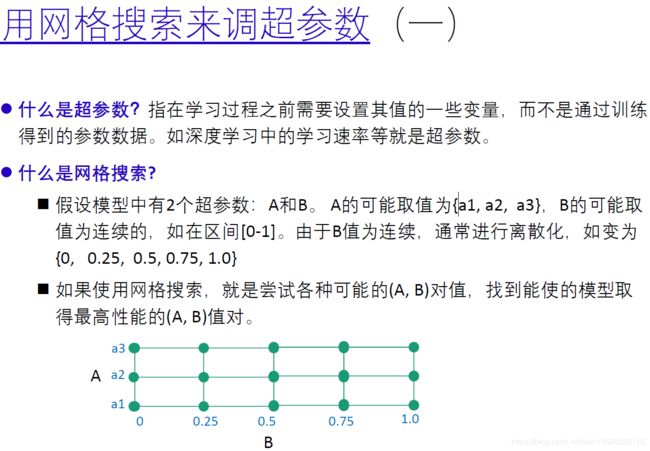

2.2. 向量范数矩阵范数
2.2.1. 向量范数

- 补充: L 0 L_0 L0 范数:向量中非 0 0 0 元素的个数;在稀疏表示中有用到(希望参数中有很多的 0 0 0);一般讲的真正的稀疏化加的约束就是 L 0 L_0 L0 范数,但是 L 0 L_0 L0 范数真正的稀疏化,但 L 0 L_0 L0 这个东西求不出来;因此有用 L 1 L_1 L1 范数逼近的。

2.2.2. 矩阵范数
