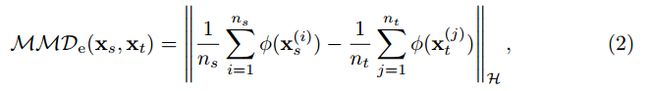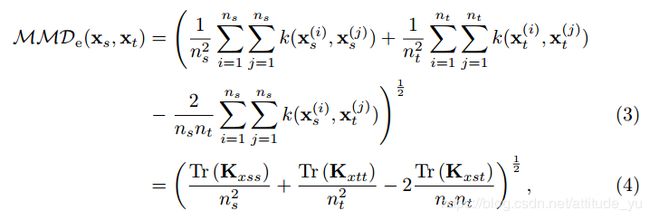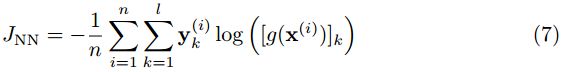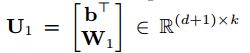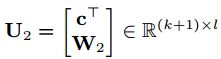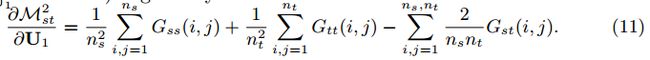DaNN详解

1.摘要

       本文提出了一个简单的神经网络模型来处理目标识别中的域适应问题。该模型将最大均值差异（MMD）度量作为监督学习中的正则化来减少源域和目标域之间的分布差异。从实验中，本文证明了MMD正则化是一种有效的工具，可以为特定图像数据集的SURF特征建立良好的域适应模型。本文代表了在神经网络背景下对MMD度量的初次研究。

2.研究背景及意义

       在基于机器学习算法的计算机视觉中，训练样本与测试样本之间的分布存在差异是真实场景下的基本问题。例如，假设本文有一个从包含具有特定视角、背景和变换条件的目标的训练集中学习的目标识别器；然后将其应用于具有类似目标的环境，但其具有不同的视角、背景和变换条件。由于缺乏表示新目标环境的标签数据或者与目标有关的知识不足。如果使用传统学习方法进行训练，则无法保证可以准确的识别，这是因为其不满足机器学习训练集和测试集独立同分布的假设条件。解决领域间分布差异的方法即为迁移学习。迁移学习按照属性集是否相同进行划分，分为同构迁移和异构迁移，则本文所研究的域适应就是同构，即源域和目标域的属性集相同。

        域适应问题描述：假设给定一个训练集和测试集分别从分布Ds和Dt中采样，任务目标是关于yt的信息不足，当Ds！= Dt时预测此目标标签yt。

        在图像识别中，Office数据集已成为评估域适应模型性能的标准图像集。这个数据集的标准评估协议是基于使用SURF特征描述符作为模型的输入。但是，使用这种描述符通常需要人工仔细设计才能获得良好的判别特征。因此，它可能会在实时特征提取过程中带来更多的复杂性，所以本文使用可自动提取特征的神经网络模型。

       在深度学习中，经常在训练模型之前进行利用ImageNet训练参数进行预训练，其对于深度神经网络的成功发挥了重要作用。但是，其并不能解决分布存在差异的问题。

        本文提出了一个简单的神经网络域适应模型，利用非参数概率分布距离度量，即最大平均差异（MMD）作为嵌入在监督反向传播训练中的正则化。MMD用于减少由从不同域抽取的样本导致的两个隐藏层之间的分布。本文是当前首次在神经网络中使用MMD。具体而言，本文将研究MMD正则化是否可以提高神经网络的域适应性能。

3.算法框架

3.1最大均值差异度量

        最大平均差异（MMD）是来自其样本的两个概率分布之间差异的度量。给定数据集X上的两个概率分布p和q，MMD被定义为：

        其中，F是一类函数f：X->R，定义为通用再生核Hilbert空间（RKHS）中的函数集合，用H表示。当MMD=0将检测到p和q之间没有分布差异。

        xs和xt是分别从数据空间X上的分布Ds和Dt得出的数据向量。可以将MMD的经验估计重写为:

         其中，φ:X->H被称为特征空间映射。

         通过将（2）转换成向量-矩阵乘法形式，得到核化方程:

       其中， k（xi; xj）是数据空间中的所有可能核。

       在域适应或迁移学习中，MMD已被用于减少源域和目标域之间的分布存在差异问题。本文在这里的研究采用了将MMD整合到学习算法中的想法，基于监督学习使用MMD正则化，在监督训练中的MMD正则化将产生更好的判别特征。

3.2前向传播

       前馈神经网络（FFNN）已被广泛用于解决过去几十年中的许多分类任务，包括目标识别。标准FFNN结构由三种类型的层组成：输入层，隐藏层和输出层。

        本文则考虑一个单独的隐藏层神经网络，其中x，h和o分别作为输入层，隐藏层和输出层。本文将W1和W2 表示为相邻层之间的连接权重，其中b和c分别是隐藏层和输出层的偏差。FFNN可以写成：

        其中，σ1和σ2是非线性激活函数，本文使用的是softplus函数σ1和softmax函数σ2。目前已经认为函数σ1比函数σ2更具生物合理性（2011年的结论）。一些实验工作证明σ1激活函数可以提高神经网络模型的性能（2010年的结论）。此外，利用softmax函数获得FFNN输出层概率预测。

        给定n个标记的训练数据; y代表每个类有一个输出节点的标签，FFNN以对数似然损失函数形式表示的目标函数为(7)，这通常通过反向传播算法来最小化。

3.3域适应神经网络

        本文提出一种标准前馈神经网络的变形，称之为域适应神经网络（DaNN），将MMD度量（2）作为嵌入在监督反向传播训练中的正则化。通过使用这种正则化训练网络参数，使目标领域在监督训练中得到优化，并使得隐藏层在表示不同领域间保持不变。

        给定标记的源数据和未标记的目标数据，单层DaNN的损失函数由下式给出：

       其中，JNNs是与式（7）相同的损失函数，仅适用于源域数据；qs，qt是激活函数前的线性组合输出；γ是正则化常数控制MMD对损失函数contribute的重要性。

       为了最小化（8），需要计算JDaNN的梯度。在计算JNNs的梯度时，计算MMD2的梯度则取决于核函数的选择。本文选择通用的高斯核核函数KG，其中s是标准差。

       本文可以用高斯核函数的矩阵向量形式来重写（8）中的MMD函数；x（s）和x（t）表示样本向量；将样本与偏差结合起来，重新定义参数矩阵U1和U2。因此，MMD函数可以重写为：

         其中，的梯度是：(黑点是s或者t)

         的梯度则可表示为：

4.训练过程

        在实现中，本文将JNNs和MMD2的最小化分为两步。首先，使用关于U1更新的小批量随机梯度下降来最小化JNNs。小批量数据集已经成为神经网络训练中的标准操作，以在速度和准确性之间建立折中。然后，通过相对于梯度（11）重新更新U1，使MMD2最小化。 后一步是通过全批量梯度下降完成的。伪代码如下：

4.1超参数

        实验中使用的DaNN模型只有一个隐藏层，即由256个隐藏节点组成的浅层网络；输入层可以是原始像素或SURF特征；输出层包含十个与十个类对应的节点。

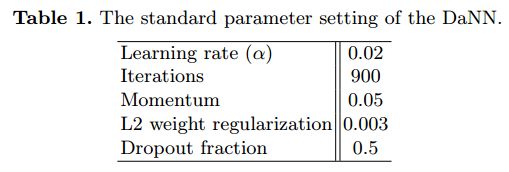
         在本文的所有实验中，本文使用表1中指定的监督反向传播学习的参数数据集。

       本文还采用dropout正则化,以一定概率随机省略每个训练样本的隐藏节点。

        如果神经网络是从小型训练集中训练的，就可以在减少过拟合的情况下产生更好的性能。

        计算高斯核的标准偏差s：s=pow(MSD/2,0.5)，其中MSD是所有源样本之间的中值平方距离。MMD正则化常数γ设置为足够大（γ= 10e3）。

4.2实验结论

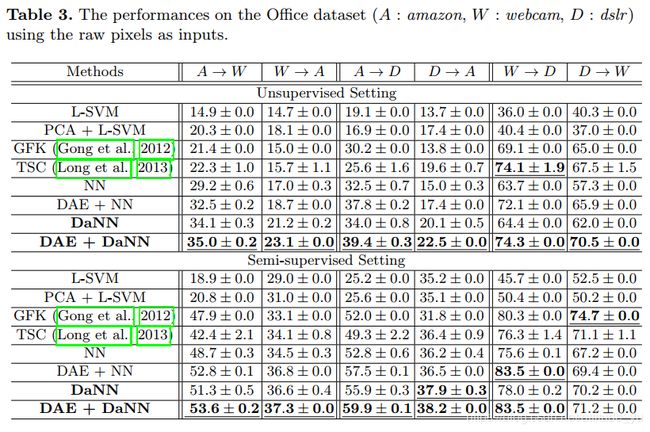
       很明显，与基于SVM的模型和NN模型相比，本文的DaNN总是可以提供所有域对中的准确性改进。 换句话说，MMD正则化确实提高了神经网络的性能。

5.总结

       本文使用自适应神经网络（DaNN）来减少目标识别中的分布差异问题,利用MMD度量作为监督反向传播训练中的正则化，使得隐藏层分布彼此相似。证明了DaNN在Office图像集上表现良好，特别是在原始图像像素上作为输入。

       有待研究的问题，尽管MMD正则化的有效性，但仍有许多方面可以进一步改进。本文已经看到，在特征学习方法中主要关注的原始像素的性能仍然不如SURF特征上的性能。另外，关于计算域适应问题的MMD的内核选择的研究可能是值得解决的。

6. 代码实现