设计一个十进制纯机械乘法器,继续大数乘法
缘由
周六的一个下午和今天一个早上,终于写完了本文。昨天上午用纸板子做了个简单的机械行列选择机,被问起为什么,我说我不喜欢电子的东西,我喜欢能hold住全场的,毕竟电子的东西我搞不定电池和各种门电路…自制发电机又没有漆包线,好吧,拆马达即可…马达既可以发电,又可以被电驱动,你要是担心自己搞不定足以发电的转速,反着用减速齿轮不就是个加速齿轮吗?
正文
上一篇文章描述了大数乘法的基本思路和我的一些思考:
计算机大数乘法引发的思考: https://blog.csdn.net/dog250/article/details/102520390
然而意犹未尽,本文继续。
我想试试看怎么能设计一台直接计算十进制乘法的机械装置,不用任何通电元器件。大家都在玩互联网的时候,我却退回到了机械,仅仅觉得好玩。
本文将介绍一些更有意思的东西。
程序员写文章,数学公式可以没有,但一定要有代码,不然会被笑话。所以,本文还是有完整代码的。
我们还是先从一个简单的问题开始:
- 计算机计算 “ 873456 × 3456876 873456\times 3456876 873456×3456876” 和 “ 3 × 4 3\times 4 3×4”,哪个更快?
试试看是最直接的了。我们先写个代码比较一下上述两个乘法的计算耗时:
#include 然后我们分别用相对大的数字和相对小的数字来计算10000乘法:
[root@localhost ]# ./a.out 10000 873456 3456876
long result=67074368 elapsed time=23 us
[root@localhost ]# ./a.out 10000 3 4
long result=12 elapsed time=24 us
时间几乎是一致的。可以简单得说:
- 计算机并不会因为乘数的数位短而运行的更快。
这有悖于我们的直觉!在我们看来,越长的数字不是需要越多的步骤来计算吗?比如我们用竖式计算。
事实上,我们之所以在竖式计算时会感觉数字越短计算越快是因为我们可以 “一眼” 识别到数字的长度。我们一眼就看完了整个数字,而计算机只能枚举整个字长空间,才能确定数字的结束。
非常简洁完美,这是由二进制的性质决定的:
- 在单bit 乘以任意数字 b b b时,结果要么为0,要么为 b b b本身。
如果看不懂上面的电路图,没关系,C代码可以看懂即可。接下来我用C程序模拟一下这个乘法器的实现:
#include 可以看到,必须把 sizeof(long) 全部check完之后,才能结束计算,无论你提供的乘数的长度是1字节还是8字节。
这只是一个引子,我们不仅仅可以得到 “计算机并不会因为乘数的数位短而运行的更快。” 的结论,更重要的是,我们又找到了一种计算大数乘法的方法,即:
- 类似硬件乘法器那般机械地完成整个计算,它暴露的是乘法过程的本质。
CPU乘法器将上述基于二进制的算法硬化到了门电路里。之所以可以硬化到CPU里,完全是利用了NP/PN结的特性,它们恰好可以用通和断表示1和0!
这里引出一个新的问题:
- 这个算法可以基于十进制的硬件实现吗?
当然,这只是一个 “仅仅觉得好玩” 的问题,我并不会去真的做这么一个装置。
这种装置即便是做出来也只能欣赏一下机械之美,在现代电子计算机面前,再精致的机械计算装置只能拿来看,就像我们在博物馆看100多年前的戴姆勒梅赛德斯奔驰一样。
十进制世界没有硅可用,NP/PN结只有两个状态,我们找不到现实世界中有十个状态的物件,十个手指头显然不足以支持大规模计算,那么我们如何造一台十进制的计算机器呢。
千百年以前人们就在思考这个问题了,从算筹,算盘,到帕斯卡加法机,差分机都是这方面的勇敢尝试,阅读和研究这些资源是技术考古学的事,但是今天,我想在现代的视角下从零设计一个十进制乘法器。
经过一些思考,初步有了一个雏形,携带着我的一些思考过程,写了本文。
首先能想到的一个现成的加法器就是机械钟表。这是一个典型的3位60进制加法器!
机械钟表作为一个加法器一直在持续做 递增 加法操作,逢60进1,任意时间的时间值就是分别读时针,分针,秒针的读数叠加,读作 “H时M分S秒” ,非常类似 “a百b十c” 。
拆开机械钟表,我们发现这是一个三个不同大小的齿轮契合的传动装置,原理非常简单,比葫芦画瓢,我们就能实现一个三位十进制加法器了,把刻度按照的 10 60 \dfrac{10}{60} 6010归一即可。
早期的帕斯卡加法器差不多也是这个原理。如果我们把这种齿轮契合传动的加法装置看作是一个 十进制模拟计算装置 的话,我今天要介绍另一种截然不同的 十进制数字化计算装置 。
先来类比二进制数字系统。
前面说了,二进制的硬件实现依赖了自然界的物质硅。二极管,三极管组成的门电路刻画在硅片上形成的芯片,是数字系统的基础。
然而十进制没有硅可用!怎么办?
用齿轮啊!
齿轮是万能的,我们照着门电路的样子,用齿轮来堆积一个十进制乘法器如何?!
为了完成这个目标,先看芯片是如何进行二进制计算的。事实上,芯片不会计算,它只是一种晶体而已,之所以它看起来是会计算的,是因为人们设计了 恰好让它看起来会计算的电路 ,这个设计背后的依据就是 “真值表” 。
换句话说,芯片并不知道 10 & 11 10 \& 11 10&11 意味着什么,它并不懂布尔代数,芯片在计算 10 & 11 10\&11 10&11时是通过查内化到电路的一张表来完成的。
我们需要在装置里内化一张 “十进制真值表” 。
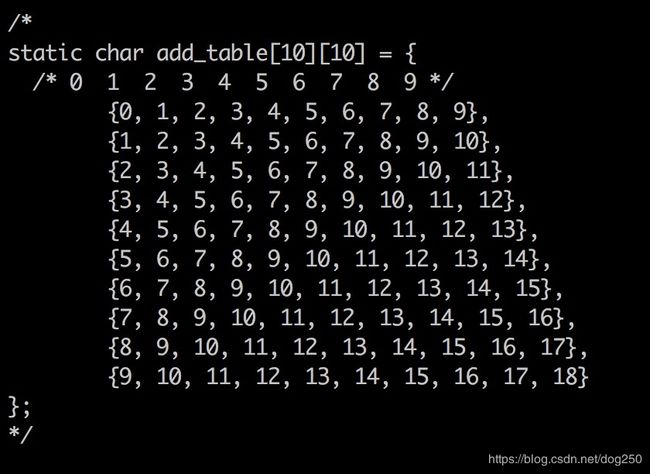
二进制的真值表基于二进制3个基本运算与,或,非而生成,而十进制基本运算又是什么呢?对于我们人而言,很显然,十进制的基本运算就是一位数加法和一位数乘法,因此,可以认为, 九九加法表和九九乘法表就是十进制的真值表。
事实上,二进制的与,或,非操作就是二进制的乘,加,取相反数。
我们指望用齿轮来传动上图的结果输出。
我们要用齿轮传动统一处理查表结果,进位等问题,所以我们可以将加法表和乘法表的结果分拆成进位和结果两部分,每一个部分都是一个一位数,于是加法表和乘法表的样子如下:
二进制电路可以用与门,非门,或门排列实现真值表,十进制如何内置九九加法表和乘法表呢?
我们需要设计一个装置,通过3维数组的前两个维度定位操作数,最后一个维度定位结果,比如,我们要找 4 + 5 4+5 4+5的结果,那么它就是:
num1 = 4;
num2 = 5;
进位 = add_table[num1][num2][0];
个位 = add_table[num1][num2][1];
乘法亦然。
因此很显然,用 行列定位装置 将会非常方便,行和列作为两个输入,其定位的矩阵单元作为输出,可以确定结果的个位和十位,个位直接输出,十位参与下一级的进位运算。
以 a n . . . a 2 a 1 × b = c m . . . c 1 a_n...a_2a_1\times b=c_m...c1 an...a2a1×b=cm...c1为例,看看一个多位数乘以一位数的乘法装置最终是什么样子:
 如果让电子元器件实现上述的乘法装置,那再简单不过了。电子装置中,九九乘法表输出的个位和十位可以轻而易举的传动到其它加法表的行或列选择杆。
如果让电子元器件实现上述的乘法装置,那再简单不过了。电子装置中,九九乘法表输出的个位和十位可以轻而易举的传动到其它加法表的行或列选择杆。
对于电子装置而言,无论是模电还是数电,所有的问题都可以转化为开关问题。想把力从A点传到B点,只需要AB导线连接,B处装控制动力的继电器,A点接通电源即可。
对于纯机械的方案,电子装置的设计思路行不通,因为纯机械装置只认识朴素的牛顿定律,不借助简单机械构件,力只能横平竖直地传导,或者借助齿轮,轮轴等圆周力,径向力,轴向力改变力的方向。
但这也正是纯机械设计的魅力之所在,如果说数电领域二极管,三极管组成的与门,或门,非门可以组成一切,那么在机械领域,齿轮,轮轴,杠杆作为基本构件,通过巧妙的组合,也能玩得五花八门。这也显示了机械设计和电子设计的另一个很有意思的区别:
- 机械设计的特点在于,大部分人都能看懂,但是却设计不出来,而电子设计则相反,没有基础的人根本看不懂,而一旦有了基础,电子设计并不是很难。
思考加法,乘法矩阵的行选列选机制花了比较久的时间,我希望的效果是 行列选择无状态。 意思是说,无论先选择行还是先选择列,均可以驱动行列交叉处的传动杆向下伸出。这对于操作而言非常友好,免除了任何时序的依赖,比如对于计算 2356 × 8 2356\times 8 2356×8而言,我可以以任何顺序按下 2 , 3 , 5 , 6 , 8 2,3,5,6,8 2,3,5,6,8这五个数字的行列选择杆,唯一的约束就是 8 8 8要作为行选,而其它数字作为列选。
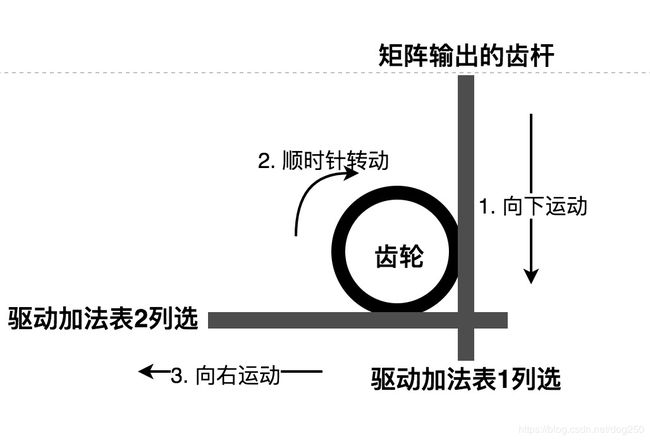
下面是我的一个设计示意图(没有机械制图软件,只能这样了)。
 我们看到,只有一根传动杆输出向下的运动,而根据加法表和乘法表可以看到,实际上有两个输出,分别对应个位和十位,这两个输出分别要驱动两个加法表的列选择,如何让一个输出变成两个呢?
我们看到,只有一根传动杆输出向下的运动,而根据加法表和乘法表可以看到,实际上有两个输出,分别对应个位和十位,这两个输出分别要驱动两个加法表的列选择,如何让一个输出变成两个呢?
上图中,还有一个细节没有标出。我们知道,乘法表或者加法表矩阵中某个元素的输出位可能是相同的,比如 1 × 3 = [ 0 , 3 ] 1\times 3=[0,3] 1×3=[0,3] 和 7 × 9 = [ 6 , 3 ] 7\times 9=[6,3] 7×9=[6,3],个位都是3,因此 ( 1 , 3 ) (1,3) (1,3), ( 7 , 9 ) (7,9) (7,9) 这两个单元的输出是相同的,能不能合并它们呢?
很难!因为啮合齿轮组是耦合在一起的,解耦非常难,需要十分精妙的trick,每一步转换都要损失传动比,为了让多个输出相互不影响,最简单的方案就是直接并联输出它们,因此对于靠乘法装置或加法装置驱动的加法器的行列选择,它们看起来是下面的样子:
 另一方面,考虑到无论是乘法表还是加法表,都是对称的,因此关于对角线对称的两个单元是可以合并的。
另一方面,考虑到无论是乘法表还是加法表,都是对称的,因此关于对角线对称的两个单元是可以合并的。
先不考虑对称合并,100个乘法单元会有100根传动杆输出,100根传动杆每一根携带一个联动齿轮,然后加法表1同样会有多根传动杆输出用于驱动加法表2的行列选择…这才是一位乘法单元,考虑到 齿轮不适合远距离传动 ,需要把如此多的零件集中在非常小的空间内!要是做出来,绝对是精密仪器!
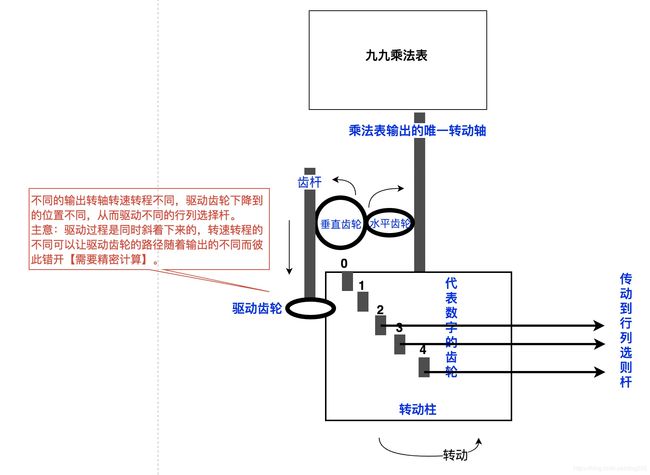
换个思路, 能不能把100根传动杆换成一根转动轴呢?设计单输出!
- 用转速和转距来表示相应的输出数字,比如转 30 30 30度表示 0 0 0, 60 60 60度表示 1 1 1 …
在乘法单元里直接将输出的数字转换成不同大小的齿轮以驱动转轴的转程,这样整个乘法表就只有两根转轴输出了,在输入到加法装置的时候,需要将转程转换回对应的数字,即用不同的转程驱动不同的行列选择杆,这也是很巧妙的:
即便如此,虽然省掉了几百根传动杆,但是乘法表内部的齿轮组却复杂了很多,加上实现驱动齿轮的逻辑,依然需要非常精密的工艺。
啮合齿轮组解耦逻辑非常复杂,解耦的最简单方案就是各自使用独立的齿轮,然而多级传动对齿轮间的最大距离,精度以及润滑的要求极高,特别是在狭小的空间内,有效传动变得更加困难。
试想,为了完成整个计算,整个装置的输入仅仅是人手指的轻微推力,靠这个轻微推力驱动如此多的齿轮,本身就是对精度和润滑的一个极大挑战。
粗旷思维驱动下,可以考虑液压,油压这种变力传动机制。
思考了一晚上,放弃了液压传动和气压传动,能称为艺术品的机械设计只用齿轮和杠杆即可完成!纯精密机械发源于古代,当时基本的橡皮管都造不出来,所以只能利用容易制造的齿轮,杠杆这种来做刚体传动,换句话说精密机械大部分都是刚体机械,就不要指望传送带,液动这种现代装置了,设计一个乘法机,结果搞成煤矿就无心插柳了。所以说,帕斯卡加法机直到今天依然是艺术品。
对了,还有中国古代的核雕,不亚于精密机械之精妙,《核舟记》里讲的。
这些都是精细的巧活儿…对于我等不是从事这个行业的人特别是搞IT互联网的来讲,只能望洋兴叹,根本那个时间来精心打磨。如果这个装置真的做出来了,那必然是奢侈品。
我自己是机械科班生。2002级黑龙江科技大学机械工程系科班出身。
我试着用纸箱的纸板做了一个 1 × 1 1\times 1 1×1矩阵,大早上五点起来搞的:
我试着对它进行操作,效果还不错。这个装置的最重要特征就是无状态,无论先选择行,还是先选择列,都能驱动红色的小棍棍向下伸出:
说明还是可行的,这是逻辑上比较麻烦的部分,剩下的就是精密传动部件的堆积了。做是做不出来了,真的好难。
我特意咨询了机械加工的费用,200mm尺寸内的精密机械,按照组件收费,这个乘法器大概需要5位到6位数人民币。我没有这么多钱。有朋友建议我搞FPGA,同样,这需要学习成本。
作为学机械出身的程序员,可以理解机械工程师巧妇难为无米之炊的痛苦,但至少你得满足其他程序员 show me the code 的诉求,不然就 cheap 了。
那就用代码写出来吧,这就是程序员这个职业特殊的好处,试错成本极低,有想法马上就能编码。
吾尝终日而思,不如须臾之coding也。
按照上述的机械设计,我准备将其计算逻辑用C代码展示出来。在此之前,我们先看一下简单的加法表计算加法的逻辑:
#include 可以试着用这个代码做个加法看看效果。
加法表的操作实现了,乘法表也差不多,把九九乘法表硬编码即可。
按照上面的机械逻辑,乘法运算就是不断查询乘法表和加法表的结果,当整个步骤完成后,结果也就自然而然输出来了。下面的代码模拟了整个过程:
#include 我们用这个 “本应该用机械实现的软件乘法装置” 计算一些乘法,首先来计算几个简单乘法:
[root@localhost ~]# ./a.out 34 8 1
result:272
[root@localhost ~]# ./a.out 11 8 1
result:088
[root@localhost ~]# ./a.out 11 11 1
result:121
[root@localhost ~]#
没错,符合预期。
接下来我们来计算几个大数乘法,为了验证结果的正确性,我们用bc程序做同样的计算,并对比结果:
显然,结果是正确的。
虽然 O ( n 2 ) O(n^2) O(n2)的软件性能很低,但作为一种新的乘法计算的方法,欣赏一下也可以。这就好比说,即便它真的用齿轮给凑出来了,也没人真的会用它来做乘法运算一样。这个装置的效果就是, “哇!它真的可以做乘法计算,按动几个按钮,它真的能给出结果耶!”
你可以用小卡片代替传动装置,把输出的 [ 6 , 3 ] [6,3] [6,3] 中的 3 3 3 拿到加法表的第三列,以此类推,最终可以得到正确的结果,嗯,这其实就是竖式计算过程的模拟。换句话说,该装置其实是通过一系列巧妙联动的传动装置,自动完成了竖式计算的过程,这些传动组件可谓是各抱地势,钩心斗角,类似门电路在硅片上挖沟填壑的刻画过程,非常巧妙。
计算机CPU运算的过程,也不过如此。
说回二进制和十进制。
现如今的数字系统普遍采用二进制,并不意味着二进制就是注定的,二进制成为数字系统事实的标准完全依赖地球上现成的一种物质,硅。如果没有硅,实现数字系统采用二进制并非显而易见。事实上,如果没有硅,如果不是因为发现了半导体,整个数字产业都不一定能发展起来!
所以说, 伟大的事件是硅的发现,而不是采用了二进制。 那些认为中国古代阴阳八卦就是二进制,所以二进制是必然之类的说法根本没有任何凭据。
抛开硅不说,二进制表示的效能并不是最高的,最高的应该是 e e e进制,和 e e e最接近的自然数是 3 3 3,也就是说三进制才是最高效的表示,其次才是二进制。三进制的高效是显而易见的,因为宇宙万物的任何属性都是三元的:
- 有
- 无
- 未知
所以 三进制的三态无需任何编码,又不会有任何浪费,就可以表示宇宙所有事物的所有属性特征。
然而地球上找不到天然的三态物质,幸运的是地球上有硅这种二态物质,因此将第三态 “未知” 用二态编码即可,与三进制用三态3比特(三进制的比特表示大致应该是 0 0 0, 1 1 1, X X X) 相比,二进制需要用二态4比特表示所有的状态,稍微有点浪费,但也还不错。
换句话说,二进制只是 e e e进制,三进制的退化版本,硅的发现使这种退化成为可能。否则,人们普遍采用的是其它数制,和二进制的硅一样,因为人们能够找到其它数制的天然表示物。
由于对钟表感兴趣,特意查了一下60进制的起源。虽然我知道不可能找到正确答案,但是看看别人怎么说的也是有益的。
我倒是觉得60进制和12进制有关。下面是我上周一个早上发的朋友圈:
很多资料都说古人取60是因为要按照天象记录时间,而错综复杂的天象事件周期并不一致,将周期事件画在一个圆圈上,每一类事件都会平分这个圆,而60是1,2,3,4,5,6的公倍数。但是我觉得这个解释有点牵强。
我倒是觉得60进制和人的手指头腹或者指关节数量有关。按照数指头腹的方法,一只手可以数到12,大拇指做计数指针,考虑到只有大拇指一个控制指针,只记录倍数的话两只手刚好可以数到60,这比数十个指头方便有效的多,用手指进行十进制计数没有指针,大拇指也用于计数,只能靠点头或者默念来做计数时钟。
算卦的也采用这种数指关节的方法来计算天干地支,这个也许和计时采用60进制有关。
最大化利用手指头上的组件最终连指腹都充分利用是60进制起源的最朴素解释,至于说野人为了计时,需要平分一个圆找出了1,2,3,4,5,6的公倍数60,我觉得这只是一个结果,野人的所有行为都是为了活下去,没有工夫进行归纳总结,也不会主动采用迂回的方法解决问题,但是即便是野人也有双手,利用最容易接近的东西来记录一些事件是一种自发行为。
所以,不能用现代科学的观念去评价野人的行为,否则就会犯形而上学的错误,这种思想是很危险的。
12进制的另一个应用是我们常用的计量单位 “一打” ,来一打鸡蛋,来半打生蚝…
16进制也是古代秤杆计量上普遍使用的一个数制。
在我国古代的时候,通常都是用北斗七星、南斗六星和福禄寿三星制作秤杆,秤杆上的十六个点就分别代表着它们,这十六星在秤杆上刻制成当时的“十六星花”,这十六星告诫做买卖的人们要为人实诚,不欺瞒顾客。
摘自 http://www.sohu.com/a/339029898_587798
无论使用什么数制,都有其一定的渊源,并且都是可以做成某种自动化的装置。这个过程可以总结如下:
利用身边常见的现成物件(比如手指,指腹,指关节,星座,硅这些东西)的特征确定数制,然后给予该数制一定的运算规则,利用这些物件在该规则的指导下完成一个计算步骤,比方说十进制乘法的竖式计算步骤。所谓的计算装置,就是利用一些或机械的,或电子的构件,将这些步骤联动起来实现半自动化或者全自动化操作。
不管是机械装置,还是电子装置,从野人的绳子,石子,到现代电子计算机,直到未来的量子计算机,都是这么一个过程。
再次强调,电子计算机,多亏了硅。
临近结束,思考一个问题, 什么是计算?
发动机是计算吗?输入燃油和空气,输出动力和尾气,和我们的输入两次不同位置的按力,输出一排数字有什么本质的不同吗?
来自何勇的一首歌, “吃的都是良心,拉的全是思想”
跋
浙江温州皮鞋湿,下雨进水不会胖。