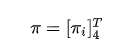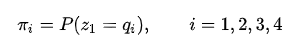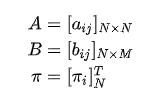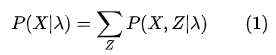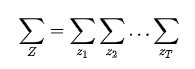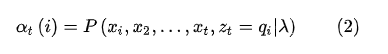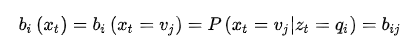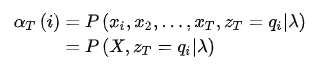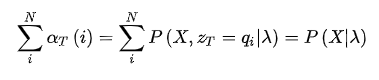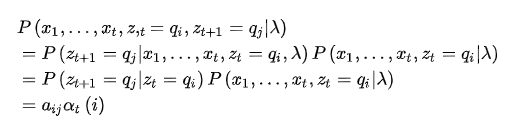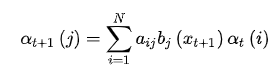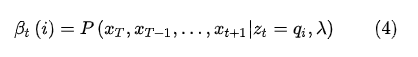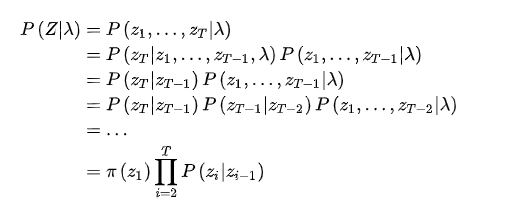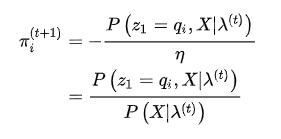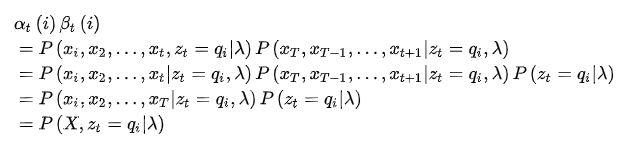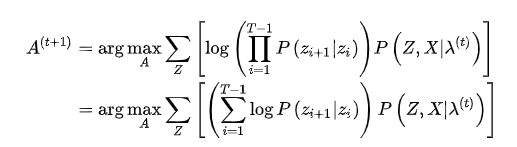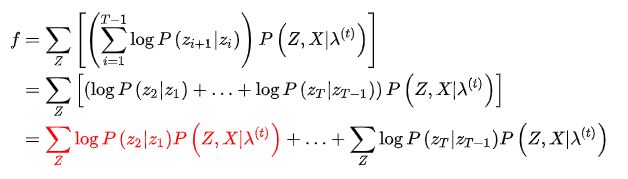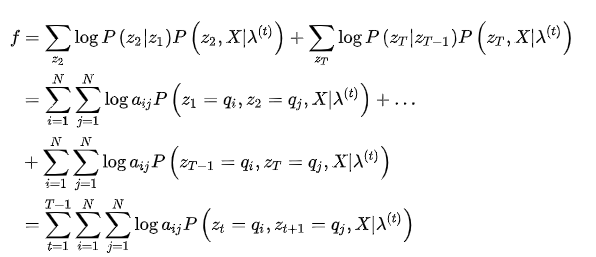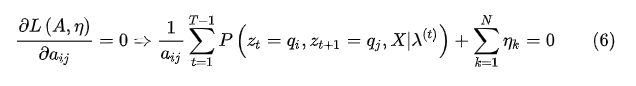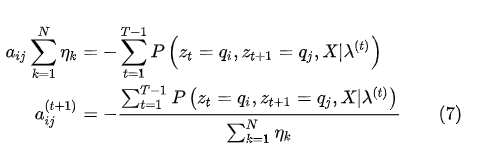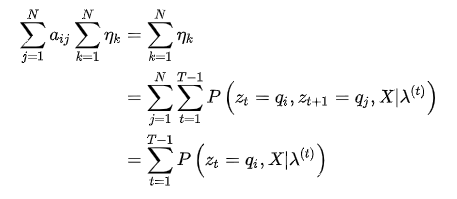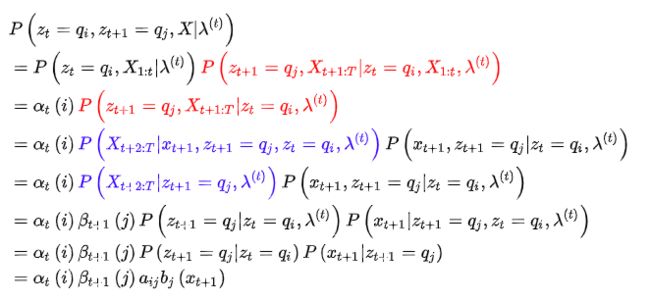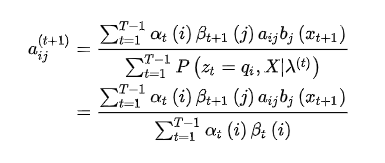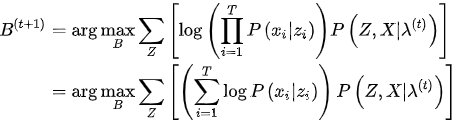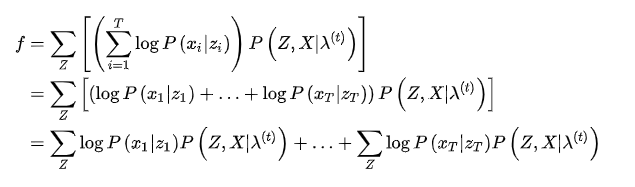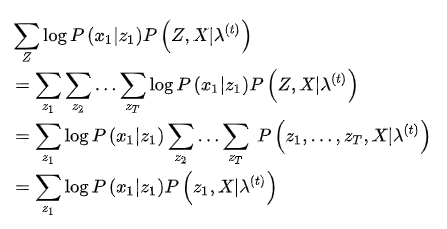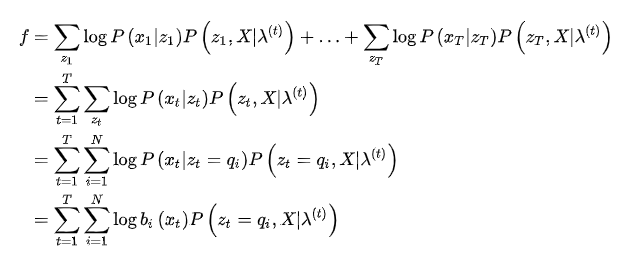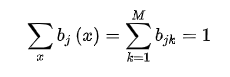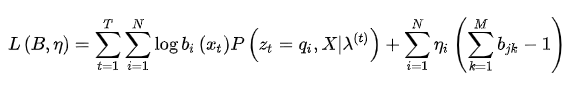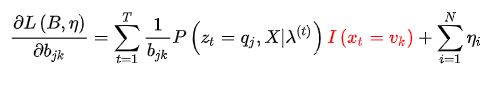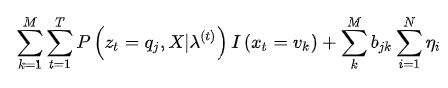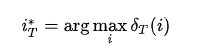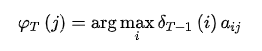一站式解决：隐马尔可夫模型（HMM）全过程推导及实现

原文链接： https://bss.csdn.net/m/zone/bdtc2019?utm_source=aicamp

作者 | 永远在你身后

转载自知乎用户永远在你身后

【导读】隐马尔可夫模型（Hidden Markov Model，HMM）是关于时许的概率模型，是一个生成模型，描述由一个隐藏的马尔科夫链随机生成不可观测的状态序列，每个状态生成一个观测，而由此产生一个观测序列。

定义抄完了，下面我们从一个简单的生成过程入手，顺便引出HMM的参数。

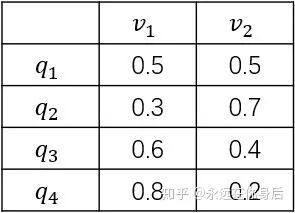
假设有4个盒子，每个盒子里面有不同数量的红、白两种颜色的球，具体如下表：

本栗子引用自《统计学习方法》

现在从这些盒子中抽取若干（  ）个球，每次抽取后记录颜色，再放回原盒子，采样的规则如下：

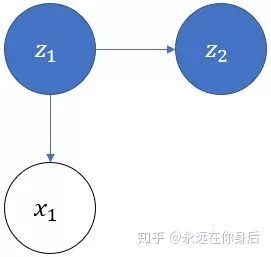
开始时，按照一个初始概率分布随机选择第一个盒子，这里将第一个盒子用  表示：

将的值用变量 表示。因为有4个盒子可共选择，所以 。然后随机从该盒子中抽取一个球，使用表示：

将 的值用变量 表示。因为只有两种球可供选择，所以 。一共有4个箱子，2种球，结合前面的箱子的详细数据，可以得到从每一个箱子取到各种颜色球的可能性，用一个表格表示：

进一步，可以用一个矩阵（称为观测概率矩阵，也有资料叫做发射矩阵）来表示该表

其中  表示在当前时刻给定 的条件下，给定

 表示当前的时刻，例如现在是第1时刻；然后是前面标注的初始概率分布，这个概率分布可以用一个向量（称作初始状态概率向量）来表示：

其中的

例如该分布是均匀分布的话，对应的向量就是

记录抽取的球的颜色后将其放回，然后在按照如下规则选择下一个盒子（）：

• 如果当前是盒子1，则选择盒子2
• 如果当前是盒子2或3，则分布以概率0.4和0.6选择前一个或后一个盒子
• 如果当前是盒子4，则各以0.5的概率停留在盒子4或者选择盒子3

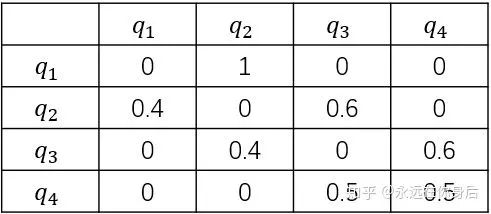
同样，也可以根据以上规则做出一个表格，其中首列表示当前盒子，首行表示下一个盒子

同样使用一个矩阵（称为状态转移矩阵）来表示上表

以上，生成过程的主要流程就介绍完了，简单概括就是：盒子，取球，盒子，取球……直到生成指定数量（T）的数据后停止。如果对这个过程还有不太理解的话，可以看看文章开头给出的关于马尔科夫链的链接。

现在，整理一下参数：有两个矩阵，一个向量：

其中N表示隐变量z的状态数量，M表示观测变量x可能的取值数量，在后面的讨论中，用 表示所有的参数。下面，根据这个栗子，写一个数据生成代码

import numpy as np	

	
class HMM(object):	
    def __init__(self, N, M, pi=None, A=None, B=None):	
        self.N = N	
        self.M = M	
        self.pi = pi	
        self.A = A	
        self.B = B	

	
    def get_data_with_distribute(self, dist): # 根据给定的概率分布随机返回数据（索引）	
        r = np.random.rand()	
        for i, p in enumerate(dist):	
            if r < p: return i	
            r -= p	

	
    def generate(self, T: int):	
        '''	
        根据给定的参数生成观测序列	
        T: 指定要生成数据的数量	
        '''	
        z = self.get_data_with_distribute(self.pi)    # 根据初始概率分布生成第一个状态	
        x = self.get_data_with_distribute(self.B[z])  # 生成第一个观测数据	
        result = [x]	
        for _ in range(T-1):        # 依次生成余下的状态和观测数据	
            z = self.get_data_with_distribute(self.A[z])	
            x = self.get_data_with_distribute(self.B[z])	
            result.append(x)	
        return result	

	
if __name__ == "__main__":	
    pi = np.array([.25, .25, .25, .25])	
    A = np.array([	
        [0,  1,  0, 0],	
        [.4, 0, .6, 0],	
        [0, .4, 0, .6],	
        [0, 0, .5, .5]])	
    B = np.array([	
        [.5, .5],	
        [.3, .7],	
        [.6, .4],	
        [.8, .2]])	
    hmm = HMM(4, 2, pi, A, B)	
    print(hmm.generate(10))  # 生成10个数据	
 	
# 生成结果如下	
[0, 0, 1, 1, 1, 1, 0, 1, 0, 0]   # 0代表红球，1代表白球

现在，参数介绍完了，数据生成过程也了解了，接下来就是解决HMM的基本问题了，一共有三个

不过，在讨论这三个问题的相关算法之前，首先要给出两个假设，在后面的推导过程中会不断的用到：

1. 齐次马尔可夫假设：即任意时刻的状态只依赖于前一时刻的状态，与其他时刻的状态无关（当然，初始时刻的状态由参数π决定）：

   

2. 观测独立假设：即任意时刻的观测只依赖于该时刻的状态，与其他无关： 概率计算算法

   

概率计算算法

现在，来看第一个问题，关于概率的计算，由于存在隐变量，所以X的边际概率需要将所有的联合概率   加和得到：

由于给出了T个观测数据，所以相应的状态也有T 个：

将（1）式中的  展开得到：

即使不考虑内部的计算，这起码也是 阶的计算量，所以需要更有效的算法，下面介绍两种：前向算法和后向算法。

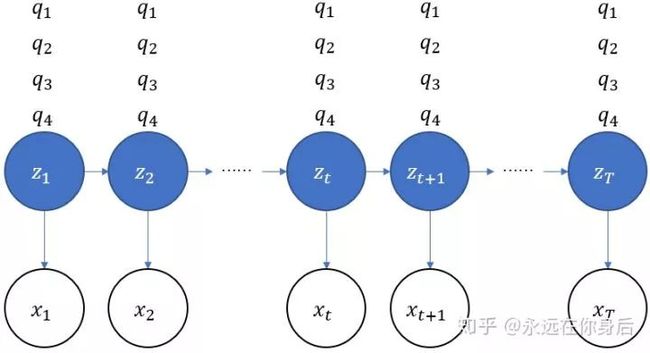
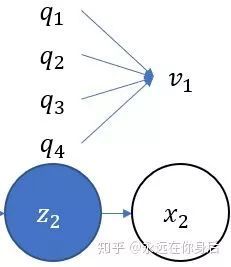
设有T 个序列，如下图所示:

现在定义一个前向概率 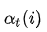 ，它t时刻的状态以及1,2,...t时刻的观测在给定参数下的联合概率：

也就是下图中标记的那一部分

根据定义，可以得到它的初值：

其中   表示由状态  生成给定观测数据的概率，例如设t时刻观测数据   ，有

接着，根据（2）式，还可以得到：

由此公式，遍历的取值求和，可以得到  的边际概率

首先，来看上式中红色部分，根据观测独立假设（下文再引用该假设时称作假设2）：

然后是蓝色部分，根据齐次马尔可夫假设（下文再引用该假设时称作假设1）

将上述结果代入（3）式，得到

以上就是前向算法的推导，下面根据一个栗子来写代码，假设前面抽了五个球，分别是：红、红、白、白、红，求概率

class HMM(object):	
    def evaluate(self, X):	
        '''	
        根据给定的参数计算条件概率	
        X: 观测数据	
        '''	
        alpha = self.pi * self.B[:,X[0]]	
        for x in X[1:]:	
            # alpha_next = np.empty(self.N)	
            # for j in range(self.N):	
            #     alpha_next[j] = np.sum(self.A[:,j] * alpha * self.B[j,x])	
            # alpha = alpha_next	
            alpha = np.sum(self.A * alpha.reshape(-1,1) * self.B[:,x].reshape(1,-1), axis=0)	
        return alpha.sum()	

	
print(hmm.evaluate([0,0,1,1,0]))   # 0.026862016

上面的注释中的代码是按照公式来写的，可以看出，时间复杂度降为了  ，比之前至少 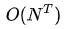 的起步价已经好太多了.

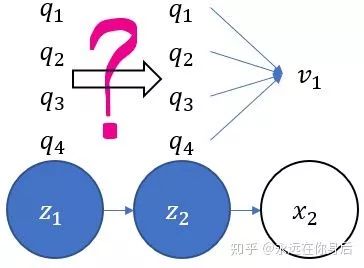
接着，再讨论后向算法，首先定义后向概率：

也就是下图中的部分

并且规定初始值

根据（4）式，还可以得到

另外说一点，如果对于前向算法还有印象的话，你会发现：上面 的定义。实际上，对于任意时刻t，存在以下等式

观察上式，蓝色部分自然就是  。而红色部分，根据假设2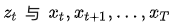， 都是无关（即互相独立），可以省去，所以这部分最终变为：

推导完毕，上代码

def evaluate_backward(self, X):	
        beta = np.ones(self.N)	
        for x in X[:0:-1]:	
            beta_next = np.empty(self.N)	
            for i in range(self.N):	
                beta_next[i] = np.sum(self.A[i,:] * self.B[:,x] * beta)	
            beta = beta_next	
        return np.sum(beta * self.pi * self.B[:,X[0]])

和前向算法差不多，而且是照着公式写的，就不写注释了，还是使用前面的栗子，跑了一下发现结果是一样的。 我想，同时写两个BUG得出同一个结果的概率应该很小很小吧

学习算法

现在，概率计算的问题就解决了，接着来看第二个问题，参数学习，这里需要用到EM算法，不熟悉的可以参考一下：https://zhuanlan.zhihu.com/p/85236423

然后，对Q函数中的每一项进行化简，首先是第一项，用到了齐次马尔可夫假设：

接着是第二项，用到了观测独立假设

又因我们要求使Q函数最大化的参数，即：

将结果代入（5）式，得到

其中，  就是当前参数下观测数据的概率，就是第一个问题所求解的。另外，利用第一个问题中定义的前向概率和后向概率，有：

最终得到：

接着来看矩阵A的迭代公式

同样，将上式化简，另外为了在后面方便引用，将该式设为一个函数f

可以看到，一共是   个相似的项，我们提一个（红色部分）出来化简，看看能不能找到通项公式

这样，就化简出了通向公式，将它代入f中，得到

因为   是一个概率分布的矩阵，例如前面的栗子，每一行的和等于1

所以A是有约束的：

同样，使用拉格朗日乘数法，构造目标函数

将该函数对矩阵A的每一个元素求（偏）导并令导数为0：

将两边同时乘上   ，得到

注意一下上面的下标t与上标中（t+1）它们是不同的，由于变量比较多，各种ijk比较多，所以这里需要注意一下。然后利用 的约束，代入（6）式，得到：

然后化简：

代入（7）式，得到

（8）式中，分母部分前面已经解决了，下面来看分子部分，进行化简

注意，上面的化简中，   。 然后红色和蓝色部分的化简用到了前面前面提过的两个假设，将条件中不被依赖的变量去掉了。最后代入（8）式得到：

最后，就剩观测概率矩阵（B）的迭代公式

同样，拆开化简

分析第一项：

代入f，得到

以前面的栗子为例，矩阵B同样有约束

也是要求每一行的和等于1

M是矩阵B的列数，前面已经定义过的，构造拉格朗日函数：

将该函数对矩阵B的每一项元素求导，得到：

同样利用B的约束条件，得到

化简得到（9）式的分母

根据上面的公式，直接敲代码了

class HMM(object):	
    def fit(self, X):	
        '''	
        根据给定观测序列反推参数	
        '''	
        # 初始化参数 pi, A, B	
        self.pi = np.random.sample(self.N)	
        self.A = np.ones((self.N,self.N)) / self.N	
        self.B = np.ones((self.N,self.M)) / self.M	
        self.pi = self.pi / self.pi.sum()	
        T = len(X)	
        for _ in range(50):	
            # 按公式计算下一时刻的参数	
            alpha, beta = self.get_something(X)	
            gamma = alpha * beta	

	
            for i in range(self.N):	
                for j in range(self.N):	
                    self.A[i,j] = np.sum(alpha[:-1,i]*beta[1:,j]*self.A[i,j]*self.B[j,X[1:]]) / gamma[:-1,i].sum()	

	
            for j in range(self.N):	
                for k in range(self.M):	
                    self.B[j,k] = np.sum(gamma[:,j]*(X == k)) / gamma[:,j].sum()	
            	
            self.pi = gamma[0] / gamma[-1].sum()	

	

	
    def get_something(self, X):	
        '''	
        根据给定数据与参数，计算所有时刻的前向概率和后向概率	
        '''	
        T = len(X)	
        alpha = np.zeros((T,self.N))	
        alpha[0,:] = self.pi * self.B[:,X[0]]	
        for i in range(T-1):	
            x = X[i+1]	
            alpha[i+1,:] = np.sum(self.A * alpha[i].reshape(-1,1) * self.B[:,x].reshape(1,-1), axis=0)	

	
        beta = np.ones((T,self.N))	
        for j in range(T-1,0,-1):	
            for i in range(self.N):	
                beta[j-1,i] = np.sum(self.A[i,:] * self.B[:,X[j]] * beta[j])	

	
        return alpha, beta	

	
if __name__ == "__main__":	
    import matplotlib.pyplot as plt	
    def triangle_data(T):   # 生成三角波形状的序列	
        data = []	
        for x in range(T):	
            x = x % 6	
            data.append(x if x <= 3 else 6-x)	
        return data	
    	
    data = np.array(triangle_data(30))	
    hmm = HMM(10, 4)	
    hmm.fit(data)               # 先根据给定数据反推参数	
    gen_obs = hmm.generate(30)  # 再根据学习的参数生成数据	
    x = np.arange(30)	
    plt.scatter(x, gen_obs, marker='*', color='r')	
    plt.plot(x, data, color='g')	
    plt.show()

上面的代码，使用最开始的栗子无法收敛，或者收敛到坑里（公式和书上《统计学习方法》是一样的），但是使用别人的例子又能很好的工作。调了一晚上后我觉得还是把它贴上来算了，希望大神发现了问题所在能告知一下。

预测算法

最后一个问题了，解决这个问题的算法叫做维特比（Viterbi）算法。实际上它是一个动态规划求解最优路径的算法，这里的最优路径不过就是对应成最大概率而已，比前面两个问题容易解决得多。直接上例子，如下图所示：

如果   ，那么最优路径（索引）自然就是

接着，假设还有   ，末端的计算自然还是一样

问题在于从  如何计算最大概率

然后，又因为我们所求的是路径，所以还要记录最大概率所对应的索引值

举个具体的例子：

最后，就是回溯最优路径，因为已知

不多说了，上代码：

class HMM(object):	
    def decode(self, X):	
        T = len(X)	
        x = X[0]	
        delta = self.pi * self.B[:,x]	
        varphi = np.zeros((T, self.N), dtype=int)	
        path = [0] * T	
        for i in range(1, T):	
            delta = delta.reshape(-1,1)     # 转成一列方便广播	
            tmp = delta * self.A	
            varphi[i,:] = np.argmax(tmp, axis=0)	
            delta = np.max(tmp, axis=0) * self.B[:,X[i]]	
        path[-1] = np.argmax(delta)	
        # 回溯最优路径	
        for i in range(T-1,0,-1):	
            path[i-1] = varphi[i,path[i]]	
        return path

（*本文为 AI科技大本营转载文章， 转 载请 联系作者 ）

◆

精彩推荐

◆

2019 中国大数据技术大会（BDTC）再度来袭！豪华主席阵容及百位技术专家齐聚，15 场精选专题技术和行业论坛，超强干货+技术剖析+行业实践立体解读，深入解析热门技术在行业中的实践落地。

即日起， 限量 5 折票 开售，数量有限，扫码购买，先到先得！

推荐阅读

• 确认！语音识别大牛Daniel Povey将入职小米，曾遭霍普金斯大学解雇，怒拒Facebook

• 大规模1.4亿中文知识图谱数据，我把它开源了

• 自动驾驶关键环节：行人的行为意图建模和预测(上)

• 不足 20 行 Python 代码，高效实现 k-means 均值聚类算法

• 巨头垂涎却不能染指，loT 数据库风口已至

• 【建议收藏】数据中心服务器基础知识大全

• 从4个维度深度剖析闪电网络现状，在CKB上实现闪电网络的理由 | 博文精选

• 身边程序员同事竟说自己敲代码速度快！Ctrl+C、Ctrl+V ？

• 100 美元一行代码，开源软件到底咋赚钱？

你点的每个“在看”，我都认真当成了AI