SqueezeNet模型解读

SqueezeNet: AlexNet-Level accuracy with 50X fewer parameters And <0.5M Model Size

论文链接：http://arxiv.org/abs/1602.07360
代码链接：https://github.com/DeepScale/SqueezeNet

Abstract

目前深度卷积神经网络主要聚焦于提升准确率，我们将要在数据集上达到某一个给定的准确率视作一个目标的话，可以实现这个目标的模型可能有很多，但是在同等精度下，更小的CNN模型至少提供了三点优势：

• 更小的CNNs模型在分布式训练期间需要跨服务器进行更少的通信；
• 更小的CNNs需要更少的带宽就可以将模型由云端导入自动驾驶汽车上；
• 更小的模型在FPGA或者其他内存有限的硬件平台上部署起来更容易；

由此我们提出了一种小型CNN结构-SqueezeNet，它在ImageNet数据集上实现与AlexNet相同的准确率，却比AlexNet需要的参数少了50倍。另外，在模型压缩技术的帮助下，我们可以将SqueezeNet压缩到0.5M以下(比AlexNet小了510倍)。

1. Introduce and Motivation

小模型的几点优势：

• 更高效的分布式训练：服务器之间的通信是分布式训练可扩展性的重要限制因素。对于分布式数据-并行训练来说，通信的开销是和模型的参数量成正比的，简而言之，小模型由于需要更少的通信所以训练的更快；
• 模型导入客户端时需要更少的花销：为了优化自主驾驶技术, 特斯拉等公司定期将新的训练模型从服务器复制到客户的车上。此做法通常称为远程更新。消费者报告发现, 特斯拉的自动驾驶仪半自主驱动功能的安全性随着最近的更新而逐步提高 (消费者报告, 2016)。然而, 今天典型的 CNN/DNN 模型频繁的远程更新可能需要大量的数据传输。与 AlexNet相比, 这将需要从云服务器传输240MB的数据量到汽车上。较小的模型只需要传输较少的数据量, 这使得频繁更新变得更加可行。
• 可行的FPGA和嵌入式平台部署：FPGA通常有不到10M的片上存储，无片外内存或存储器。对于推理而言，当视频流通过FPGA实时传输时，一个足够小的模型可以直接存储在FPGA上而不会存储器带宽所限制。进一步来讲，当在ASICs(专用集成电路)上部署CNN模型时，一个足够小的模型可以直接进行片上存储。

因此小型CNN结构有其独特的优势，这是由于这点，我们直接将问题聚焦在保证与知名模型差不多的准确率的同时，减少CNN结构的参数量。我们已经发现了这种结构-SqueezeNet，另外，我们展示了一种更加流程化的方法来搜索设计空间得到新型的CNN结构。

Section 2中描述了相关工作，接着在Section 3和4中，我们描述和评价了SqueezeNet结构，在这之后，我们将我们的注意力放到了理解CNN的结构设计选择是如何影响模型尺寸和精度的，我们通过探索类似于SqueezeNet结构的设计空间获得了一定的理解；在Section 5中，我们在CNN微观结构(单个层或模块的组织和维度)上设计了空间探索；在Section 6中，我们在CNN宏观结构上设计了空间探索；在Section 7中进行了总结。简而言之，Section 3和4对于想应用SqueezeNet的人很重要，剩下的部分对致力于设计他们自己的网络结构的人至关重要。

2. Related Work

2.1 模型压缩

这部分的内容我之前有专门写过一篇博客，感兴趣可以移步去看一下：https://blog.csdn.net/h__ang/article/details/88072278

主要的方法就是剪枝、量化、知识蒸馏等。

2.2 CNN微观结构

随着卷积神经网络越来越深，手动为每个层选择卷积核维度会非常麻烦。为了解决这个问题，由多个卷积层按照固定组织形式形成的更高等级的构建块或者模块被提出来了，举个例子，GoogleNet论文中提出的Inception模块，它就是由多个不同维度的卷积核做完卷积然后拼接形成(包括 1x1,3x3,5x5,1x3,3x1等维度的卷积核)，许多这样的模块堆叠起来，或者加上额外的ad-hoc层形成一个完整的网络，我们使用术语CNN微观结构指代具有特定组织和维度的单个模块。

2.3 CNN宏观结构

CNN微观结构指的是单个层和模块，我们将CNN宏观结构定义为多个模块的系统级组织，使其成为端到端的CNN结构。

CNN宏观结构中广泛研究的一个话题就是网络深度在CNN结构中的影响，目前认为增加网络深度是有助于提升网络模型的准确率。

跨多个层或模块的连接选择是CNN宏观结构研究中的一个重要领域，残差网络和Highway 网络都提出了跨多个层使用连接关系。举个例子，将第三个激活曾连接到第六个激活层上，我们将这种连接称为旁路连接，ResNet的作者做了一个对比实验，对一个34层的网络分别使用旁路连接和无旁路连接，实验结果显示旁路连接的网络相比之下增加了2%的准确率。

2.4 神经网络设计空间探索

神经网络(包括深度和卷积神经网络)有很大的设计空间，包含有对大量的微观结构、宏观结构、求解器和其他超参的选择。自然而然地,社区想要了解到这些因素是如何影响网络准确率的
，神经网络设计空间探索的大部分工作都侧重于开发自动化的方法, 以找到更高精度的神经网络体系结构。这些自动化(DSE)方法包括贝叶斯优化 (Snoek et, 2012), 模拟退火 (Ludermir 等, 2006), 随机搜索 (Bergstra & Bengio, 2012) 和遗传算法 (Stanley & Miikkulainen, 2002)。值得赞扬的是，每一篇论文都提供了一个案例，在这个案例中，提出的DSE方法产生了一个NN体系结构，与一个具有代表性的基础神经网络相比，它的精确度的确更高。然而, 这些论文并没有试图提供关于神经网络设计空间形状的直觉。在本文的后面, 我们避开了自动化的方法-相反, 我们通过重构 CNNs 的方式, 这样就可以做A/B的比较, 从而可以探索出CNN 架构是如何影响模型的大小和准确性的。

在接下来的部分，我们首先提出和评估了有无模型压缩的SqueezeNet结构，然后我们探索了对于类似SqueezeNet的结构，微观和宏观上的设计选择的影响。

3. SqueezeNet: preserving accuracy with few parameters

在本节中，我们首先介绍了关于构建参数较少的CNN结构的几个策略，然后我们介绍了Fire模块——我们用来CNN结构的新的模块，最后，我们使用我们的设计策略组建SqueezeNet。

3.1 结构设计策略

本片论文的总体目标就是在维持精度损失不大的条件下，确定参数很少的CNN结构。为了实现这点，我们在设计CNN结构时采用了三条主要策略：

• 策略1：使用 1x1 的卷积核替代 3x3 的卷积核。在给定确定数量的卷积核的预算下，我们要将这些卷积核中的绝大多数尺寸设置为 1x1，因为 1x1 的卷积核参数量比 3x3 的少 9倍。
• 策略2：减少 3x3 卷积核的输入通道数。考虑一个完全由 3x3 卷积核组成的卷积层，整个层的参数量为 输入feature map的通道数 x 输出feature map的通道数 x 3 x 3。所以，为了维持较小的参数量，不仅需要减少 3x3 卷积核的数量，减少其通道数也是非常重要的。在这里我们通过使用压缩层来减少 3x3 卷积核的通道数。
• 策略3：延迟网络中下采样的时间，以便卷积层可以获得较大的特征图。在卷积神经网络中，每一个卷积层都会产生一个尺寸最少是 1x1 的特征图，特征图的宽和高由输入特征图的尺寸、是否在该层进行下采样共同决定。通常来说，在CNN结构中下采样指的是在一些卷积层将步长设置为大于1的数或者应用池化层。如果在网络的前期结构中使用较大的步长，那么大多数层的特征图就会比较小；相反地，如果网络中大多数层的步长仅仅为1，步长较大的层都集中在网络的后期，那么网络中的大多数层就会有比较大的特征图。我们的一个直觉就是较大的特征图会导致较高的分类精度(在其他条件一致时)，事实也确实如此，K.He和H.Sun将延迟下采样应用到四种不同的CNN结构，在每种情况下，延迟下采样都会导致较高的分类精度。

策略1和策略2是在尽可能保留精度的同时减少CNN中的参数数量，策略3则是在有限的参数数量下最大化精度。接下来，我们介绍我们构建CNN结构的基础模块——Fire模块，这个模块同时用到了上面的策略1、2和3。

3.2 Fire模块

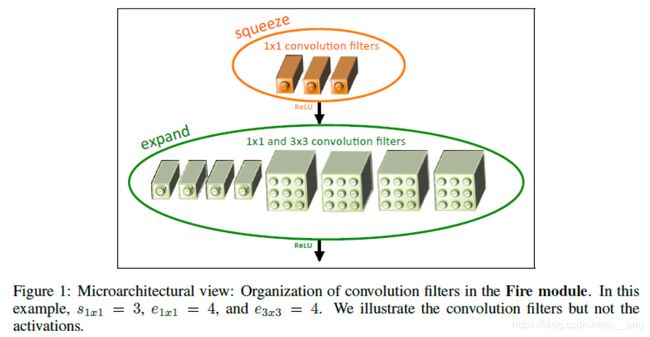
我们定义的Fire模块如Figure1中所示，一个Fire模块的第一层为一个压缩层(仅包含 1x1 卷积核)，然后送入扩张层(1x1 与 3x3 的卷积核混合使用)，我们将squeeze层1x1的卷积核数量、扩张层1x1、3x3的卷积核数量分别用s1x1、e1x1、e3x3表示，那么我们通常设置s1x1要比e1x1+e3x3小很多，这样压缩层才可以帮助减少3x3卷积层的输入通道数，吻合了策略2。

3.3 SqueezeNet结构

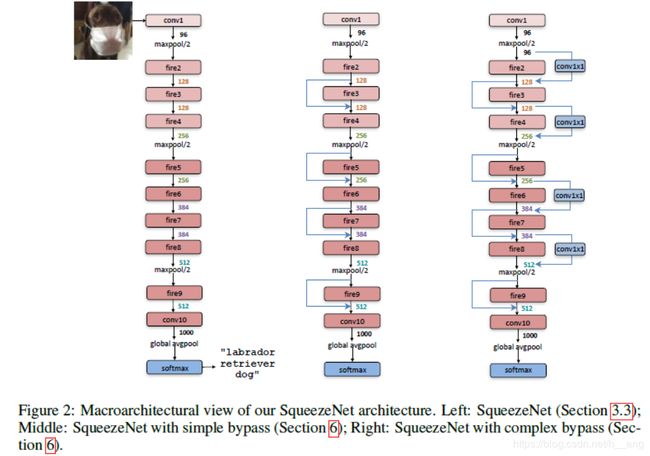
SqueezeNet网络结构如Figure 2所示，它以一个独立的卷积层开始(conv1)，后面紧跟了8个Fire模块(fire2-9)，然后最后以一个卷积层(conv10)结束。我们从网络开始到结束逐渐增加每个Fire模块中卷积核的数量，SqueezeNet在conv1、fire4、fire8和conv10之后以步长2进行最大池化操作，这些相对较晚的池化操作遵从了策略3，整个网络的结构如table1所示：


3.3.1 其他的一些细节

为了简介起见，我们在table1中省略了一些关于SqueezeNet的细节和设计选择，我们将会在接下来说的对这些设计选择进行介绍，这些选择背后的直觉可以在引用的论文中找到。

• 为了让经过 1x1 和 3x3 卷积层之后的输出特征图具有相同的尺寸，需要对要过 3x3 卷积层的输入周围做一个像素的全零填充；
• 在Squeeze层和expand层之后的激活函数都是ReLU；
• 在Fire9模块之后要过一个Drop，丢弃率设置50%；
• 在SqueezeNet中没有全连接层，这个设计选择灵感来源于NiN；
• 在训练SqueezeNet时，初始学习率设为 0.04，学习率衰减过程是线性衰减，具体细节可以参见源码；
• Caffe框架不能支持同时包含多个不同尺寸的卷积核卷积，为了实现这个操作，我们需要让输入分别过两个分支—— 1x1 和 3x3 的卷积层分支，之后将得到的输出拼接在一起；

4. Evaluation of SqueezeNet

我们现在将注意力转移到评估SqueezeNet上，目标就是压缩已经训练好的分类模型AlexNet，所以当我们评估其他相关的压缩模型结果时是以未经压缩的AlexNet模型作为基准的。

table2展示了不同模型的结果：
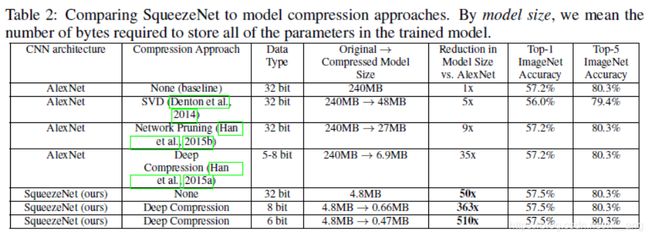上面的结果反映了Deep Compression不仅可以在参数量很大的模型上有较大的提升，它对于小模型如AlexNet来说同样可以有较好的提升。

5. CNN microarchitecture design space exploration

迄今为止，我们提出了小模型的结构设计策略，遵从这些原则我们创建了SqueezeNet，并且发现在同等精度下SqueezeNet比AlexNet小了50倍。然而，SqueezeNet或者说其他模型仍然只是未被探索的CNN设计结构中的沧海一粟。现在在Section 5和6中，我们探索了设计空间的几个方面，我们把结构探索分为两个主题：微结构探索(每个模块的组织和维度)和宏观结构(高等级端到端的模块或其他层形成的组织)。

在本节中，我们关于之前提到的三点策略，设计并执行了实验，目的是为了给微观设计空间形状提供直觉。要注意的是我们在这里的目的不是在每个实验中最大化精度，而是去理解CNN结构选择在模型大小和精度方面的影响。

5.1 CNN微观结构超参数
5.2 Squeeze Ratio，即SR

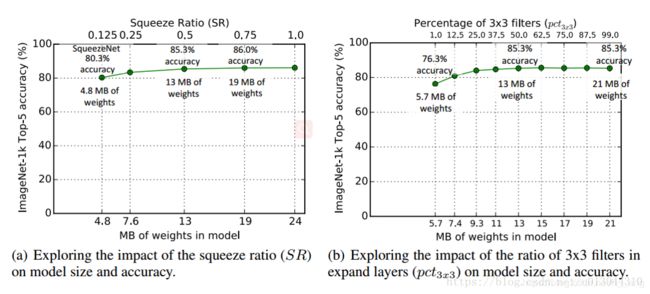
我们现在设计实验来调查 SR是如何影响模型尺寸和准确率的，我们使用Figure 2作为一个起点，其他的参数设置和table1中的相同，basee = 128, incre = 128, pct3x3 = 0.5, freq = 2。我们训练多个模型，每个模型的SR在[0.125, 1.1]之间变化。正如Figure 3(a)中所示，我们展示了实验的结果，图上的每一个点都是一个从头开始训练的独立的模型。SR = 0.75（a 19MB model）时准确率最高，即使将SR提升到1.0之后准确率再也没有提升。

5.3 1x1 和 3x3卷积核之间的平衡

在Section 3.1中，我们提出了通过用 1x1 的卷积核取代 3x3 的卷积核来减少参数数量，一个开放的问题是，在CNN卷积核中空间分辨率到底有多重要？

在这里我们试图通过调整 1x1 和 3x3 卷积核的相对比例来观察它是如何影响模型尺寸和准确率的。我们用到的参数为basee = 128, incre = 128, freq = 2, SR = 0.5。我们将pct3x3从1%变化到99%，观察到的实验结果如Figure 3(b)所示，随着pct3x3的增大模型尺寸和准确率都在增加，pct3x3 = 0.5时准确率就达到了峰值，之后继续增加pct3x3只有模型尺寸会增加，精度不再变化。

6. CNN macroarchitecture design space exploration

目前为止我们已经在微观层次探索了设计空间(CNN单个模块的内容)。现在，我们探索设计决策，主要是关于Fire模块高等级的连接关系。受到ResNet的启发，我们探索了三个不同的结构：

• Vanilla SqueezeNet（和之前的结构一样）
• 在一些Fire模块之间采用简单的旁路连接的SqueezeNet
• 在剩下的Fire模块之间采用复杂的旁路连接

三种SqueezeNet的不同变体如Figure 2所示，我们在Fire模块3、5、7和9的输入和输出之间添加了旁路连接，这几个模块就可以在输入和输出之间学习到一个残差函数。正如在ResNet中，为了可以在Fire3的输入输出之间添加简单的旁路连接，这就要求Fire3的输入(Fire2模块的输出)和输出通道数是一致的，Fire4模块的输入就等于Fire2模块的输出和Fire3模块的输出进行元素级相加。这点就像正则化应用到了Fire模块的参数上(如果Fire模块的权重几乎全零那么就相当于恒等映射，一定程度上就相当于正则化的效果)，可以提高最终的模型精度。

一个限制的地方在于简单的旁路连接要求该Fire模块的输入和输出通道数是相同的，这就意味着Figure 2(a)中只有一半的Fire模块可以进行简单的旁路连接(Figure 2(b))。当Fire模块的输入输出通道数不同时，我们使用Figure 2©中复杂的旁路连接—带有1x1的卷积核来使得该模块的特征通道上的维度可以匹配。要注意的是复杂的旁路连接会给模型带来额外的参数，而简单的旁路连接就不会。

除了正则化的效果以外，还有一种直觉上的感受就是有助于减轻squeeze层引入的瓶颈，在SqueezeNet中，SR为0.125，这意味着每个模块中的squeeze层的通道数是整个expand层的1/8。由于这样严重的维度缩减，只有很少的信息穿过了squeeze层，然而旁路的引入打开了信息的通道使得信息可以在squeeze层间流动。

我们对Figure 2中的三种宏观结构进行训练，比较了它们的尺寸和精度如table3所示，在整个宏观结构探索期间微观结构的参数和table1中的保持一致。我们发现，简单和复杂旁路的引入都有助了提高SqueezeNet的精度，有趣的地方是，简单的旁路连接竟然比复杂旁路连接的精度更高。

7. Conclusions

我们希望SqueezeNet能够激发读者的思考和考虑探索CNN架构设计领域的广泛可能性,并以更系统的方式去探索。