【LeetCode】面试算法总结@动态规划
面试算法总结:动态规划
- 前言
- 1、LeetCode----70. 爬楼梯
- Solution1
- Solution2
- 2、LeetCode----120. 三角形最小路径和
- 错误的示范
- 基本思路
- 3、LeetCode----152. 乘积最大子序列
- 基本思路
- 4、LeetCode----121. 买卖股票的最佳时机
- 基本思路
- 5、LeetCode----122. 买卖股票的最佳时机 II
- 基本思路
- 6、LeetCode----123. 买卖股票的最佳时机 III
- 基本思路
- 思路推广到可以买卖k次
- 7、LeetCode---- 300. 最长上升子序列
- 基本思路
- 8、LeetCode----322. 零钱兑换
- 基本思路
前言
江湖人层流传着这样语句话,互联网行业笔试得动态规划着得天下,哈,活跃以下气氛。但是动态规划在面试算法中真的很重要,应该引起足够的重视才行的。
1、LeetCode----70. 爬楼梯
https://leetcode-cn.com/problems/climbing-stairs/
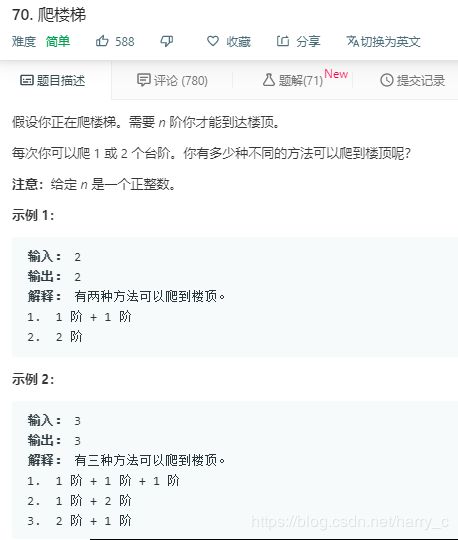
Solution1
#首先想到使用递归来求解
#最终写下代码如下,但是时间复杂度明显太大,我们必须进行优化,下面使用动态规划算法求解
class Solution1(object):
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
if n == 0:
return 0
if n == 1:
return 1
if n == 2:
return 2
return self.climbStairs(n-1) + self.climbStairs(n-2)
Solution2
#使用动态对话的思路,首先不要将动态规划想的这么玄乎,其实他的基本思想并没有高瞻远瞩的规划思想
#其基本的思路就是在递归的基础上进一步思考以空间复杂度换取时间复杂度
#将前面的计算结果存储到一个设定的空间就会大幅度缩减递归算法的重复计算
#其实本体的基本思想与斐波拉契数列是类似的,找到一个递推式f(n) = f(n-1) + f(n-2)
#使用上面的递推式我们可以进行求解直接一个for循环就能够递推出我们最终要求得的n对应的答案
#当然还应该处理一些特殊的情况初始状态是ans[0] = 1、ans[1] = 1、ans[2] = 2
#其实本题还可以再进行优化,我们存储的可以不是整个数组,而是n前的两个数而已
class Solution2(object):
def climbStairs(self, n):
if n==1 or n==0:
return 1
ans = [0] * (n + 1)
ans[0] = 1
ans[1] = 1
ans[2] = 2
for i in range(2, n + 1):
ans[i] = ans[i - 1] + ans[i - 2]
return ans[n]
2、LeetCode----120. 三角形最小路径和
https://leetcode-cn.com/problems/triangle/
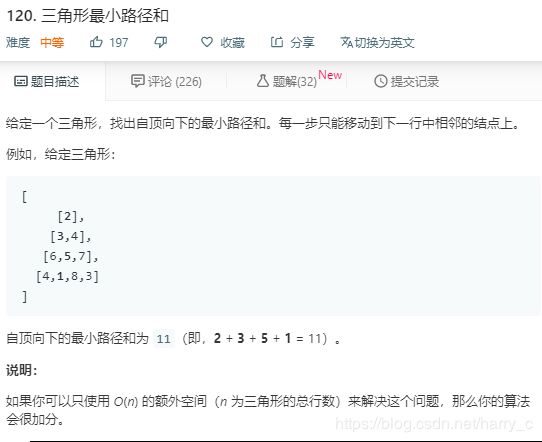
错误的示范
#这是一个错误的例子,使用的是贪心算法,但是本题使用贪心算法并不能解决问题
class Solution(object):
def minimumTotal(self, triangle):
"""
:type triangle: List[List[int]]
:rtype: int
"""
ans = triangle[0][0]
for i in range(1, len(triangle)):
check = 0
temp = min(triangle[i][check], triangle[i][check+1])
check = triangle[i].index(temp)
ans += temp
return ans
基本思路
#首先将列表的最后一行存储赋值到ans中,然后通过两层循环进行遍历
#第一层循环i,表示的是每一层,有最后一层和已经使用无需再进行遍历,所以遍历由len(triangle)-2遍历到第0层
#第二层循环j,表示遍历每一层i中的所有元素
#我们使用的递推式:ans[j] = min(ans[j], ans[j+1]) + triangle[i][j] 表示的是遍历每一层,并将所有层次的累加和加到对应的位置,
#使用min(ans[j], ans[j+1])也是使用贪婪算法的思想,但是由下而上的这种算法是可以达到全局最优的
#最终我们将计算的最小的结果传递存储到ans的第一个数,也就是ans[0],就是我们最终存储的答案。
class Solution(object):
def minimumTotal(self, triangle):
"""
:type triangle: List[List[int]]
:rtype: int
"""
if not triangle:
return
ans = triangle[-1]
for i in range(len(triangle)-2, -1, -1):
for j in range(len(triangle[i])):
ans[j] = min(ans[j], ans[j+1]) + triangle[i][j]
return ans[0]
3、LeetCode----152. 乘积最大子序列
https://leetcode-cn.com/problems/maximum-product-subarray/

基本思路
#再次强调的是,看到一个算法题或者是一个算法需求的时候,我们应该要认真规划好算法,认真读需求或者审题。
#本题通过仔细审题之后大家应该不难发现,我们记录最大值,其实每次只要记录最小值或者最大值即可
#每次存储之前的最大值和最小值,等到遍历下一个num的时候回将其进行更新,通过min(pre_min*num, num, pre_max*num)
#求当前的最小值,类似的通过max(pre_min*num, num, pre_max*num)的最大值
#而我们最终需要的答案是从现在的最大值和之前已经计算的最大值之中选择一个最大的
#如此反复迭代,最终能够求得我们整个空间的最大值
class Solution(object):
def maxProduct(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if not nums:
return
pre_min = nums[0]
pre_max = nums[0]
ans = nums[0]
for num in nums[1:]:
now_min = min(pre_min*num, num, pre_max*num)
now_max = max(pre_min*num, num, pre_max*num)
ans = max(ans, now_max)
pre_min = now_min
pre_max = now_max
return ans
4、LeetCode----121. 买卖股票的最佳时机
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/

基本思路
#首选我们只能交易一次,所以找到的是从最低点买入最高点卖出,所以应该首先找到价格的最低点进行存储
#存储之后,我们通过遍历所有的价格,每次都求当前价格与最低价格的差即为收益
#最低收益为之前最低收益与当前收益中的最大值,依次迭代
#最终求得的就是最高的收益
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
min_p = prices[0]
ans = 0
for i in prices:
min_p = min(min_p, i)
ans = max(ans, i-min_p)
return ans
5、LeetCode----122. 买卖股票的最佳时机 II
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/submissions/

基本思路
#本题虽然基于上一题可以增加了购买最多次的条件,其实解题思路变得更加明白了
#我们只要每天都买进卖出(检查买进卖出收益是否大于0,否则不进行操作)
#如此进行迭代,就能够将所有的收益收入囊中并且实现收入的最大化。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
answer = 0
n = len(prices)
for i in range(n):
if i+1 == n:
break
if prices[i+1] - prices[i] >= 0:
answer = answer + prices[i+1] - prices[i]
return answer
6、LeetCode----123. 买卖股票的最佳时机 III
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iii/

基本思路
#本题难点在于股票可以买卖两次
#所以我们应该像之前一样,构建买卖两次的价格存储空间
#第一次买卖的收益记录的是当前最高的收益,第二次买卖的收益则是基于第一次的最大收益进行买卖的最大收益
#得到四个递推公式,按照股票价格进行迭代,最终求得的第二次卖的收益就是全局买卖两次的最大收益
#其实这种方法是可以推广到可以买卖k次的下面是扩展推广
class Solution(object):
def maxProfit(self, prices):
#第一次买收益,第一次卖收益,第二次买收益,第二次卖收益
bq = [[float('-inf'), 0], [float('-inf'), 0]]
for i, price in enumerate(prices):
bq[0][0] = max(bq[0][0], - price)
bq[0][1] = max(bq[0][1], bq[0][0] + price)
bq[1][0] = max(bq[1][0], bq[0][1] - price)
bq[1][1] = max(bq[1][1], bq[1][0] + price)
return bq[1][1]
思路推广到可以买卖k次
#思想基本一致
#我们创建第一次第二次。。。第k次的买卖的收益
#然后使用一个for循环对每次的买卖价格进行更新
#最外层的for循环遍历股票价格,最终第k此卖出的收益就是我们全局的买卖k次的最大收益
class Solution(object):
def maxProfit(self, prices, k = 2):
if k == 0:
return 0
bq = [[float('-inf'), 0] for _ in range(k)]
for i, price in enumerate(prices):
for j in range(len(bq)):
if j+1 == k:
break
bq[j][0] = max(bq[j][0], - price)
bq[j][1] = max(bq[j][1], bq[j][0] + price)
bq[j+1][0] = max(bq[1][0], bq[j][1] - price)
bq[j+1][1] = max(bq[j+1][1], bq[j+1][0] + price)
return bq[-1][-1]
7、LeetCode---- 300. 最长上升子序列
https://leetcode-cn.com/problems/longest-increasing-subsequence/
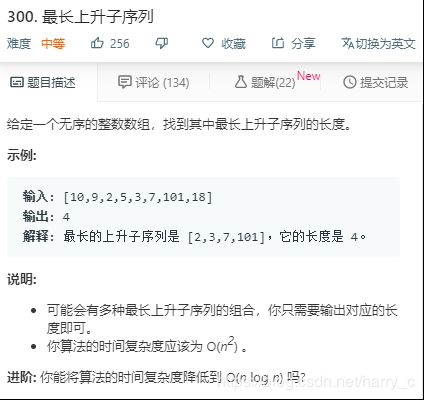
基本思路
#这一题其实并不是很难,但是就是调试磨了好久才通过测试
#首先我们应该定义一个ans表示的是第i个的元素的最长子升序序列。
#为什么这样定义呢,因为本题是符合最优子序列的,下一个元素的最长升序子序列,必定基于它的上一个也是最长升序序列
#首先我们通过遍历nums,每次遍历到一个num将其与前面所有的数进行比较,小于前面的数时,将目前值与前面值加一赋值给当前
#最终求解ans中所有的最大的数返回则是我们要求的最长升序子序列
class Solution(object):
def lengthOfLIS(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if not nums:
return 0
ans = [1] * len(nums)
for i in range(len(nums)):
for j in range(0, i):
if nums[j] < nums[i]:
ans[i] = max(ans[i],ans[j] + 1)
return max(ans)
8、LeetCode----322. 零钱兑换
https://leetcode-cn.com/problems/coin-change/
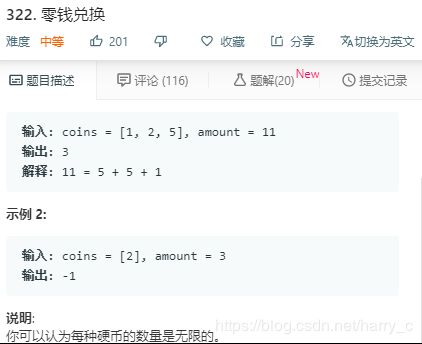
基本思路
#本题读题的第一反应可能是设ans[i]为每个序号为i的硬币
#作为最大钱数组成的对应金额的最少硬币数
#但这种dq设计并不能有一个好的递推公式
#还是忍不住看了别人的思路才知道,可以把ans[i]设置为对应目标金额为i时的最少硬币数,i最大为amount+1
#这样设置的好处是我们可以找到一个递推公式ans[i] = min(ans[i], ans[i-coin] + 1)遍历所有的硬币
#找到一个硬币coin,前面计算过的为i-coin,基于ans[i-coin]+1,就可能是我们目前的最小硬币数
#然后求min(ans[i], ans[i-coin] + 1)反馈的结果就是所求的最小硬币数
class Solution(object):
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
ans = [float('inf')] * (amount + 1)
ans[0] = 0
for i in range(len(ans)):
for coin in coins:
if i - coin >= 0:
ans[i] = min(ans[i], ans[i-coin] + 1)
return ans[-1] if ans[-1] != float('inf') else -1