【LeetCode】面试算法总结@递归
面试算法总结:递归
- 1、 LeetCode----50. Pow(x, n)
- 基本思路
- 2、LeetCode----169. 求众数
- 基本思路
- 3、LeetCode----121. 买卖股票的最佳时机 I
- Solution1
- Solution2
- 4、LeetCode----122. 买卖股票的最佳时机 II
- 基本思路
- 5、LeetCode----22. 括号生成
- 基本思路
1、 LeetCode----50. Pow(x, n)
https://leetcode-cn.com/problems/powx-n/submissions/
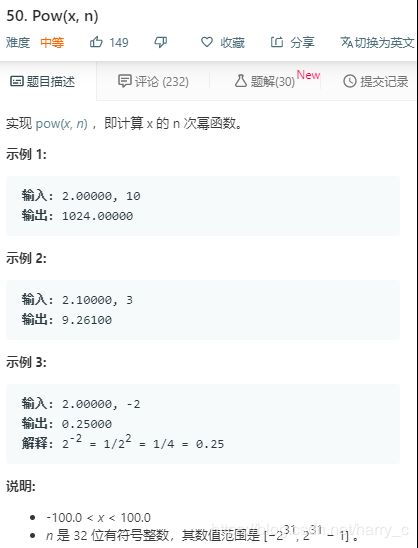
基本思路
#首先判断是否符合条件,若果n为0则返回1,如果n为-1,则返回1/x
#然后通过递归求解使用每次整除2的方法,递归之后,判断n的奇偶性,如果为偶数,则答案为其平方
#如果为奇数,则答案除了平方之外还应该乘以一个x。
#依次递归返回最终答案
class Solution:
def myPow(self, x: float, n: int) -> float:
if not n:
return 1
if n == -1:
return 1/x
answer = self.myPow(x, n//2)
if n % 2:
return x * answer * answer
else:
return answer * answer
2、LeetCode----169. 求众数
https://leetcode-cn.com/problems/majority-element/
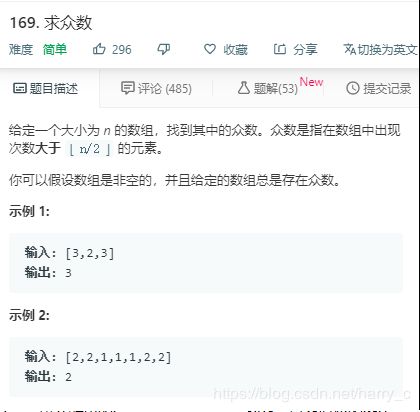
基本思路
#首先求众数应该要把每一种数统计出来个数。
#统计出来的个数存储到字典中,然后进行遍历。
#每次都要保存最大的value,以及对应的key
#最后得到的key就是我们要找的众数。
class Solution:
def majorityElement(self, nums: List[int]) -> int:
check = {}
for num in nums:
try:
check[num]
except:
check[num] = 0
check[num] += 1
tem_key = ''
tem_value = 0
for key,value in check.items():
if value >= tem_value:
tem_key = key
tem_value = value
return tem_key
3、LeetCode----121. 买卖股票的最佳时机 I
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/
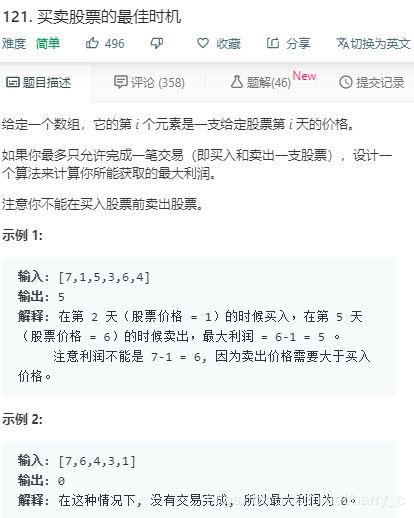
Solution1
#暴力法,利用两层循环直接进行暴力破解,当然有需要优化的地方
#如果第一个数的后两个数都比前一个小,那么此数无需进入第二层的循环
#依次暴力求解出最优的内容
#这显然不是一个好的方法
class Solution1:
def maxProfit(self, prices: List[int]) -> int:
answer = 0
check = 999999999
for i in range(len(prices)):
if i+1 ==len(prices):
break
if prices[i] <= check:
check = prices[i]
if prices[i] <= check and prices[i+1] <= check:
continue
for j in range(i, len(prices)):
if prices[j] - prices[i] >= answer:
answer = prices[j] - prices[i]
return answer
Solution2
#仔细观察发现,最高的收益等于max(当前收益,当前价格-之前最低价格)
#所以可将算法的时间复杂度优化到O(n),使用依次循环遍历
#每次求解出两个值,一个是历史最低价,一个是历史最高收益。
#依次遍历求解,所得即为所有股票价格中最高的一次收益价钱。
class Solution2:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
min_p = prices[0]
ans = 0
for i in prices:
min_p = min(min_p, i)
ans = max(ans, i-min_p)
return ans
4、LeetCode----122. 买卖股票的最佳时机 II
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/
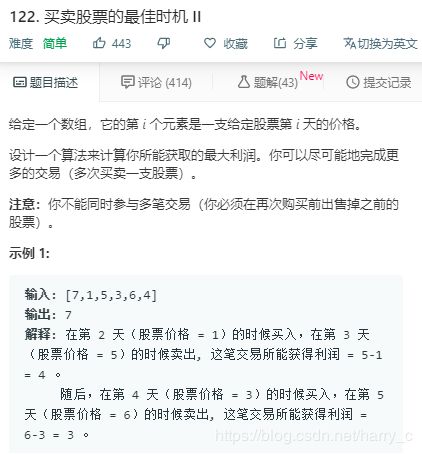
基本思路
#对于题给的信息我们知道,股票操作无限次数,没有交易费用。
#很明显是一个贪心算法的例程
#通过遍历价格列表
#我们将每天的价格与下一天的价格求差值,大于0,则可以产生收益。加入到我们的收益中去
#依次遍历求解,最终求得的结果肯定是我们所能获得的最大收益率。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
answer = 0
n = len(prices)
for i in range(n):
if i+1 == n:
break
if prices[i+1] - prices[i] >= 0:
answer = answer + prices[i+1] - prices[i]
return answer
5、LeetCode----22. 括号生成
https://leetcode-cn.com/problems/generate-parentheses/submissions/、

基本思路
#在做题之前应该先好好思考问题,避免一看到题目就以为自己想到思路的,结果很有可能是一个无法完成的方案。
#首先想到的是使用递归算法,本题的递归算法其实还是稍微有点绕的。
#我们可以这样想,把括号当成是n个左括号,n个右括号一次填入到一个盒子中,但是我们一个个保证括号是配对的。
#首先肯定是取一个左括号添加到盒子中,接着我们可以添加左括号也可以添加又括号,但是要保证一些基本的规则。
#首先括号是成对出现的,所以我们剩余的左括号的数量肯定应该比右括号的数量低的。
#其次不管左括号还是又括号个数都是小于n的,所以当一家用了n个的时候我们不能继续使用此括号
#最后是想如何将生成的括号序列添加到答案中呢,我们使用了self定义变量,当两种种类的括号都已经使用完毕的时候,并且都是在以上条件下使用的,#此时就是我们应该生成的括号,将其添加到我们的括号列表中即可
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
self.ans = []
self.create(n, n, '')
return self.ans
def create(self, left, right, result):
if left == 0 and right == 0:
self.ans.append(result)
return
if left > 0:
self.create(left - 1, right, result + '(')
if right > 0 and left < right:
self.create(left, right - 1, result + ')')