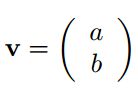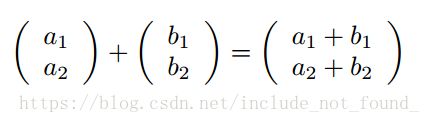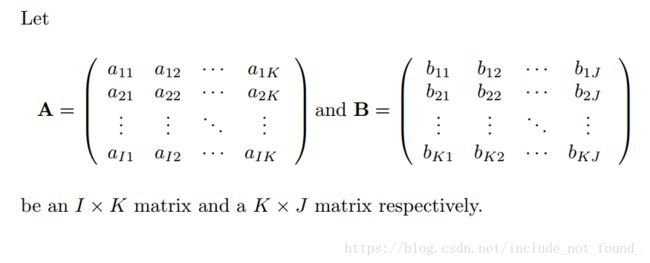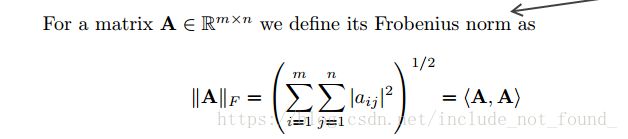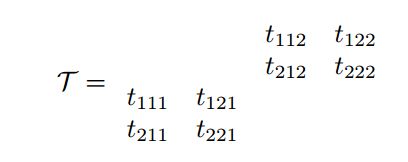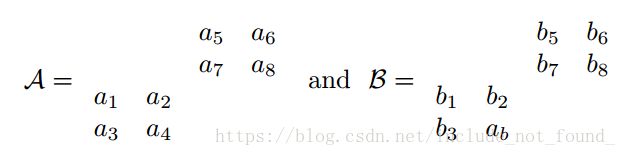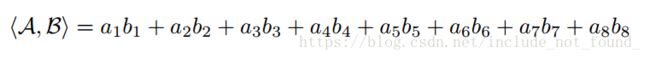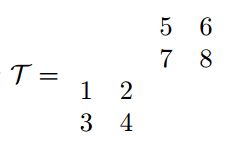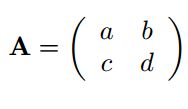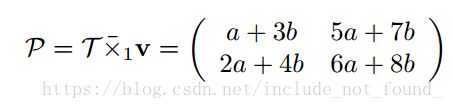向量、矩阵、张量基础知识

前言
学习并且做这篇笔记目的：学习张量，初步了解张量分解（tensor decomposition）领域。
那么什么是张量分解呢？研究它具体的应用是什么？
为了便于理解，我们先从矩阵分解讲起。
我们知道现在的数据大部分都是以矩阵形式存储的。然而在收集数据或者处理数据时总会有矩阵元素丢失的情况。这个时候矩阵分解就可以派上用场了。矩阵分解的另一个例子是根据矩阵中已有数据值去预测未知位置的值。比方说我们要做一个推荐系统，假设我们把每一个用户的偏好设为一行，我们现在已经有大量用户的偏好数据，现在来了一个新用户（即新的一行），但只有部分偏好值，我们可以通过矩阵分解来填充缺失值。

如图

但是现实中的数据往往特征很多，维数很高，我们一般用高维张量来表示。
而传统的方法是把高维张量展开（类似于flatten）成二维矩阵。但是这样处理会使数据的空间结构信息丢失，使得最终结果往往出现问题。所以我们能不能直接使用张量存储信息并且通过张量分解的方式解决上述问题呢？

---

一、向量

1.定义

只有一行或者一列的数组被称作为向量。因此我们把向量定义为一个一维数组。我们用黑体的小写字母来表示向量。

2.向量加法

对应位置元素相加即可。

3.向量乘法

▪内积（Inner product）
对应位置元素相乘之后再累加得出结果。

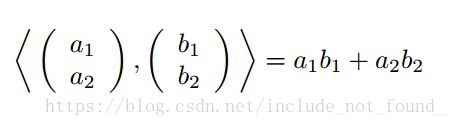
可以看到内积的结果是一个标量。

▪外积(Outter product)
使用符号 ◦ 表示

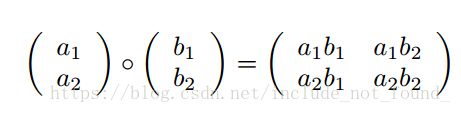
外积的结果是一个矩阵。

注：此处的外积是线性代数中的外积而非解析几何中的外积（叉乘Cross Product）

4.范数以及标准化
我们使用范数来衡量一个向量的长度。将一个向量变换为单位长度的操作叫做标准化。

▪欧几里得范数(Euclidean Vector Norm)

---

二、矩阵
矩阵使用大写粗体字体定义。

1.定义
我们定义一个二维矩阵A，有m行n列。

2.矩阵加法
大小相同的矩阵做加法对应位置元素相加即可。

3.矩阵乘法

▪普通向量乘法
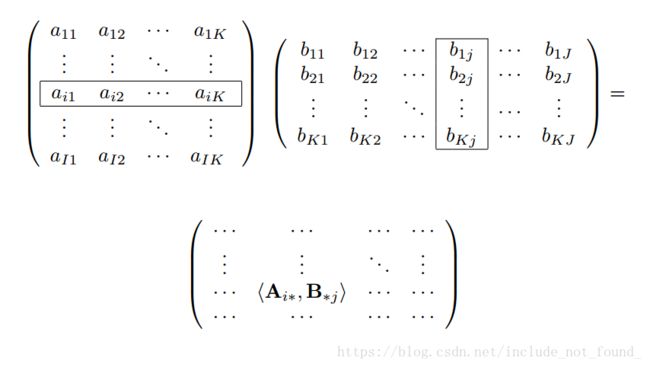
最为人熟知的矩阵乘法。

尖括号表示向量乘法。乘出来的矩阵大小为I*J。

▪Hadamard Product
符号为 ∗ ，两个矩阵大小需相同

对应位置的元素直接相乘作为一个新的矩阵。

▪Kronecker Product
符号为 ⊗

▪Khatri-Rao Product

A中的元素和B中对应的每一列相乘。
假设A和B都是向量的话，那么Khatri-Rao Product和Kronecker Product的结果是一样的。

▪Matrix Scalar Product

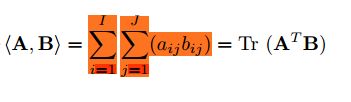
对应位置上的元素最终相加。结果为标量。

4.矩阵的范数
常用的是Frobenius范数。

5.逆矩阵
给出等式 Ax = b。如何求解？
一个直接的方法是在等式两边同时乘上A的逆矩阵

然而直接求逆只有在矩阵满足方阵，非奇异且行列式值不为0的情况下才可行。
对于一般的矩阵，我们采用伪逆矩阵来近似逆矩阵。

A为一个m*n的矩阵，秩为n时采用上面一个式子求逆，秩为m时采用下面一个式子求逆。
然而，求逆是一个不连续的函数，在计算时有可能会导致数值计算错误。

---

三、张量

1.定义
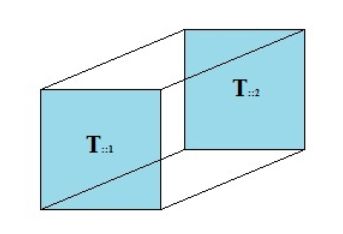
三维以及以上的数组我们称作为张量，在这里我们只研究三维的2*2*2张量。
值得一提的是，虽然张量应用在心理学，计量学和信号处理等领域仅有几十年的时间，但是它的数学理论在19世纪就已经被提出。
张量在本文中采用书法艺术字体来表示，如
我们可以将一个三维向量可视化，类似一个管道。

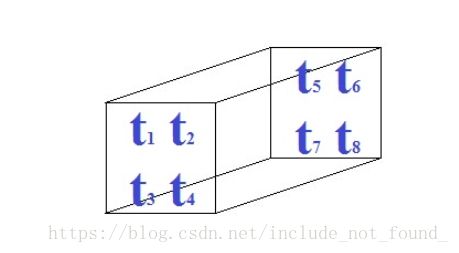
采用数据表示为

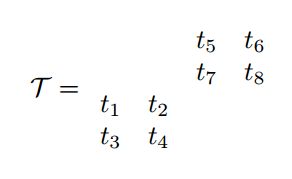
矩阵采用行和列来确定一个元素，我们也需要采用某种方式来确定某个位置的元素，我们可以使用三个索引的方式。

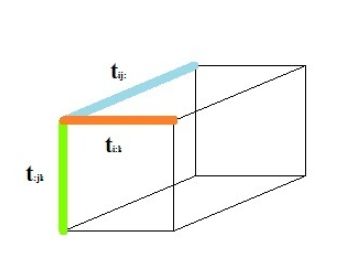
▪（纤维束）Fibers
我们固定三个索引中的两个索引来定义一个Fibers。
-张量的行定义为mode-1 fibers,符号为

-张量的列定义为mode-2 fibers，符号为

-剩下的维度定义为mode-3 fibers，符号为

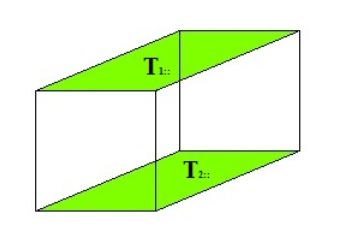
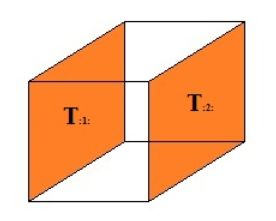
▪（切片）Slices
固定三个索引中的一个索引，得到一个平面，我们称之为slice

固定第一个索引：

固定第二个索引：

固定第三个索引：

因此我们可以将一个2*2*2张量以三个索引下标表示为

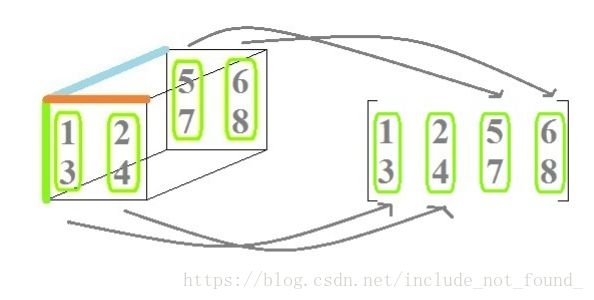
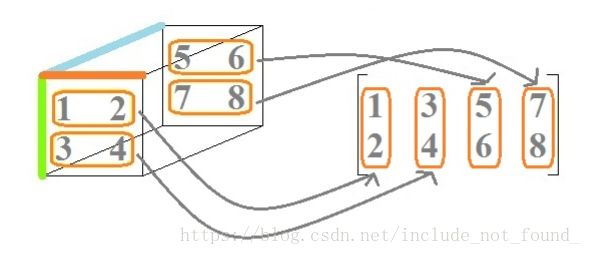
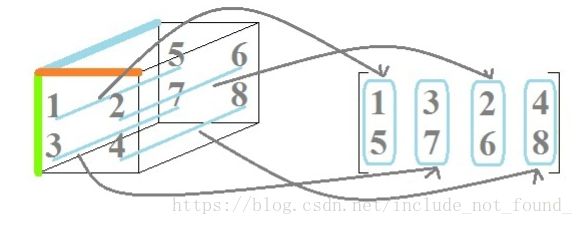
2.矩阵化
矩阵化就是将一个张量变换成一个矩阵。可以根据fiber的方向来进行不同的句矩阵化。
假如我们有下面一个张量：

mode-1 Matricization:

mode-2 Matricization:

mode-3 Matricization:

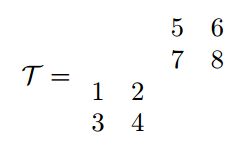
3.张量乘法
我们可以定义三种不同的张量乘法，分别是
- 同样大小的张量相乘，乘积为表来那个
- 张量乘以矩阵
- 张量乘以向量

▪ 张量内积

▪ 张量乘以矩阵
先将张量矩阵化，再将张量和矩阵相乘。不同的mode-n矩阵化会使得相乘结果不同。
乘法过程可用下图表示：

例子：如果我们有一个张量

和一个矩阵

我们对张量进行mode-1 matricization得到

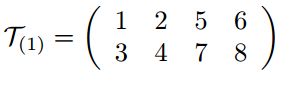
再将得到的矩阵和矩阵A相乘

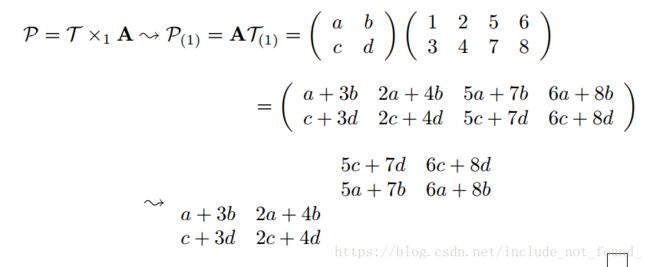
▪ 张量乘以向量
跟张量乘以矩阵类似，要将张量矩阵化。
假设还是上面的那个张量，给定的向量为

则1-mode matricization后与该向量相乘得到的结果为

4.张量的范数
张量的Frobenius范数：