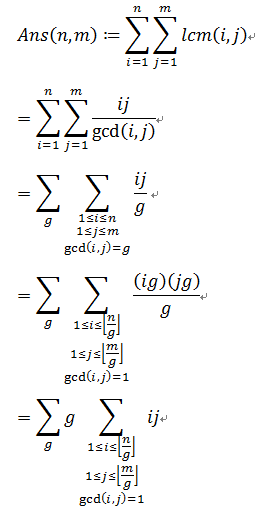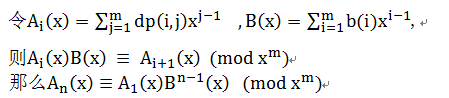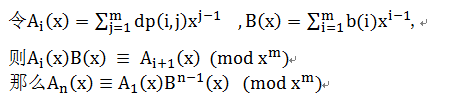题目：
http://www.lydsy.com/JudgeOnline/problem.php?id=2154
http://www.lydsy.com/JudgeOnline/problem.php?id=2693
（发题解攒RP啦~~~本来这两题一直拖着没写的，然后LJT大神问了之后没事就去想了一下，顺便A掉除除草嗯，这次要写一篇详细题解！（谁叫我是数论渣渣。。。））
大意是给定n,m求sigma(lcm(i,j))1<=i<=n,1<=j<=m，2154只处理一个查询，2693要求多个查询 N,M<=1000W
首先还是暴力的来推一推公式嗯，还是公式最明了了嗯：
10dfa9ec8a136327a8aaa8f9938fa0ec09fac7b1.jpg.png
考虑求解：
0ff41bd5ad6eddc44ad53b3e3bdbb6fd536633c0.jpg.png
那么
0ff41bd5ad6eddc44ad53b3e3bdbb6fd536633c0.jpg.png
再来考虑求最终答案：
0ff41bd5ad6eddc44ad53b3e3bdbb6fd536633c0.jpg.png
事实上到了这一步之后就可以求解2154了，在求F(n,m)中分块，在求Ans(n,m)中也分块处理，这样的时间复杂度是O(sqrt(n)*sqrt(n))=O(n)，用线性筛法求u(d)d^2（u(d)表示莫比乌斯函数），总复杂度仍然是O（n），但是这样没法做到快速支持多组查询，所以还要继续化简：
0ff41bd5ad6eddc44ad53b3e3bdbb6fd536633c0.jpg.png
然后我们惊奇的发现H（D）是可以用线性筛顺便求出，那么对D分块，处理出一个H（D）的前缀和，这样就可以在O（sqrt(n)）的时间内处理出一个询问了，所以总复杂度是O(n)-O(sqrt(n))，这样就可以解决2693啦。
代码：
2693:
#include
#include
#include
using namespace std ;
typedef long long ll ;
const ll maxn = 10100000 ;
const ll maxt = 10100 ;
const ll mod = 100000009 ;
bool flag[ maxn ] ;
ll p[ maxn ] , pn = 0 , query[ maxt ][ 2 ] , t , mn = 0 ;
ll H[ maxn ] , pre[ maxn ] ;
inline void Init( ) {
for ( ll i = 0 ; i ++ < mn ; ) flag[ i ] = true ;
H[ 1 ] = 1 ;
for ( ll i = 2 ; i <= mn ; ++ i ) {
if ( flag[ i ] ) {
p[ ++ pn ] = i , H[ i ] = ( - ( ( i * i ) % mod ) + i + mod ) % mod ;
}
for ( ll j = 1 ; j <= pn && i * p[ j ] <= mn ; ++ j ) {
flag[ i * p[ j ] ] = false ;
if ( i % p[ j ] ) H[ i * p[ j ] ] = H[ i ] * H[ p[ j ] ] % mod ; else {
H[ i * p[ j ] ] = ll( p[ j ] ) * H[ i ] % mod ; break ;
}
}
}
pre[ 0 ] = 0 ;
for ( ll i = 0 ; i ++ < mn ; ) pre[ i ] = ( pre[ i - 1 ] + H[ i ] ) % mod ;
}
inline ll sum( ll n , ll m ) {
return ( ( n * ( n + 1 ) / ll( 2 ) ) % mod ) * ( ( m * ( m + 1 ) / ll( 2 ) ) % mod ) % mod ;
}
#define sumh( l , r ) ( ( pre[ r ] - pre[ l - 1 ] + mod ) % mod )
inline ll solve( ll n , ll m ) {
ll ans = 0 ;
if ( n > m ) swap( n , m ) ;
for ( ll i = 1 , j , v ; i <= n ; ) {
j = min( n / ( n / i ) , m / ( m / i ) ) ;
v = ( sumh( i , j ) * sum( n / i , m / i ) ) % mod ;
( ans += v ) %= mod ;
i = j + 1 ;
}
return ll( ans ) ;
}
int main( ) {
scanf( "%lld" , &t ) ;
for ( ll i = 0 ; i ++ < t ; ) {
scanf( "%lld%lld" , query[ i ] , query[ i ] + 1 ) ;
mn = max( mn , max( query[ i ][ 0 ] , query[ i ][ 1 ] ) ) ;
}
Init( ) ;
for ( ll i = 0 ; i ++ < t ; ) printf( "%lld\n" , solve( ll( query[ i ][ 0 ] ) , ll( query[ i ][ 1 ] ) ) ) ;
return 0 ;
}
2154:
#include
#include
#include
using namespace std ;
typedef long long ll ;
const ll maxn = 10100000 ;
const ll maxt = 10100 ;
const ll mod = 20101009 ;
bool flag[ maxn ] ;
ll p[ maxn ] , pn = 0 , query[ maxt ][ 2 ] , t , mn = 0 ;
ll H[ maxn ] , pre[ maxn ] ;
inline void Init( ) {
for ( ll i = 0 ; i ++ < mn ; ) flag[ i ] = true ;
H[ 1 ] = 1 ;
for ( ll i = 2 ; i <= mn ; ++ i ) {
if ( flag[ i ] ) {
p[ ++ pn ] = i , H[ i ] = ( - ( ( i * i ) % mod ) + i + mod ) % mod ;
}
for ( ll j = 1 ; j <= pn && i * p[ j ] <= mn ; ++ j ) {
flag[ i * p[ j ] ] = false ;
if ( i % p[ j ] ) H[ i * p[ j ] ] = H[ i ] * H[ p[ j ] ] % mod ; else {
H[ i * p[ j ] ] = ll( p[ j ] ) * H[ i ] % mod ; break ;
}
}
}
pre[ 0 ] = 0 ;
for ( ll i = 0 ; i ++ < mn ; ) pre[ i ] = ( pre[ i - 1 ] + H[ i ] ) % mod ;
}
inline ll sum( ll n , ll m ) {
return ( ( n * ( n + 1 ) / ll( 2 ) ) % mod ) * ( ( m * ( m + 1 ) / ll( 2 ) ) % mod ) % mod ;
}
#define sumh( l , r ) ( ( pre[ r ] - pre[ l - 1 ] + mod ) % mod )
inline ll solve( ll n , ll m ) {
ll ans = 0 ;
if ( n > m ) swap( n , m ) ;
for ( ll i = 1 , j , v ; i <= n ; ) {
j = min( n / ( n / i ) , m / ( m / i ) ) ;
v = ( sumh( i , j ) * sum( n / i , m / i ) ) % mod ;
( ans += v ) %= mod ;
i = j + 1 ;
}
return ll( ans ) ;
}
int main( ) {
t = 1 ;
for ( ll i = 0 ; i ++ < t ; ) {
scanf( "%lld%lld" , query[ i ] , query[ i ] + 1 ) ;
mn = max( mn , max( query[ i ][ 0 ] , query[ i ][ 1 ] ) ) ;
}
Init( ) ;
for ( ll i = 0 ; i ++ < t ; ) printf( "%lld\n" , solve( ll( query[ i ][ 0 ] ) , ll( query[ i ][ 1 ] ) ) ) ;
return 0 ;
}