深度学习之PyTorch——Deep NN实现手写MNIST数字分类

MNIST 数据集

mnist 数据集是一个非常出名的数据集，基本上很多网络都将其作为一个测试的标准，其来自美国国家标准与技术研究所, National Institute of Standards and Technology (NIST)。 训练集 (training set) 由来自 250 个不同人手写的数字构成, 其中 50% 是高中学生, 50% 来自人口普查局 (the Census Bureau) 的工作人员，一共有 60000 张图片。 测试集(test set) 也是同样比例的手写数字数据，一共有 10000 张图片。

每张图片大小是 28 x 28 的灰度图，如下：

                                   

所以我们的任务就是给出一张图片，我们希望区别出其到底属于 0 到 9 这 10 个数字中的哪一个。

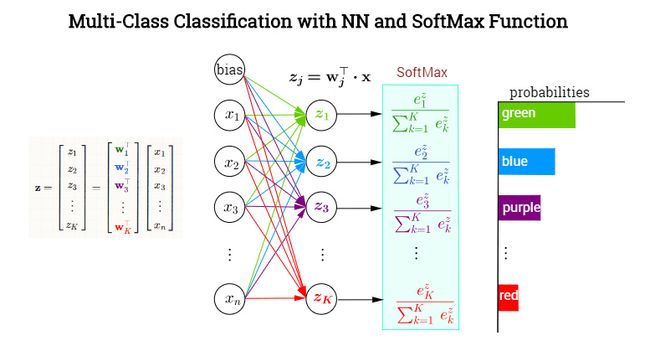
softmax

交叉熵

对于多分类问题，这样并不行，需要知道其属于每一类的概率，这个时候就需要 softmax 函数了。

                    

对于网络的输出 ，我们首先对他们每个都取指数变成 ，那么每一项都除以他们的求和，也就是

                                                                                     

如果对经过 softmax 函数的所有项求和就等于 1，所以他们每一项都分别表示属于其中某一类的概率。

交叉熵

交叉熵衡量两个分布相似性的一种度量方式，前面讲的二分类问题的 loss 函数就是交叉熵的一种特殊情况，交叉熵的一般公式为

                                             

对于二分类问题我们可以写成

                                             

 

import numpy as np
import torch
from torchvision.datasets import mnist

from torch import nn
from torch.autograd import Variable
from torch.utils.data import DataLoader
from torchvision import transforms
from torch import optim
# 使用内置函数下载mnist数据集
train_set = mnist.MNIST('./data',train=True)
test_set = mnist.MNIST('./data',train=False)

# 预处理=>将各种预处理组合在一起
data_tf = transforms.Compose(
                [transforms.ToTensor(),
                transforms.Normalize([0.5],[0.5])])

train_set = mnist.MNIST('./data',train=True,transform=data_tf,download=True)
test_set = mnist.MNIST('./data',train=False,transform=data_tf,download=True)

train_data = DataLoader(train_set,batch_size=64,shuffle=True)
test_data = DataLoader(test_set,batch_size=128,shuffle=False)

net = nn.Sequential(
        nn.Linear(784,400),
        nn.ReLU(),
        nn.Linear(400,200),
        nn.ReLU(),
        nn.Linear(200,100),
        nn.Linear(100,10))

criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(),1e-1)

nums_epoch = 20

# 开始训练
losses =[]
acces = []
eval_losses = []
eval_acces = []

for epoch in range(nums_epoch):
    train_loss = 0
    train_acc = 0
    net.train()
    for img , label in train_data:
        img = img.reshape(img.size(0),-1)
        #print(img.shape)
        img = Variable(img)
        label = Variable(label)
        
        # 前向传播
        out = net(img)
        loss = criterion(out,label)
        # 反向传播
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        # 记录误差
        train_loss += loss.item()
        # 计算分类的准确率
        _,pred = out.max(1)
        num_correct = (pred == label).sum().item()
        acc = num_correct / img.shape[0]
        train_acc += acc
    
    losses.append(train_loss / len(train_data))
    acces.append(train_acc / len(train_data))
    
    eval_loss = 0
    eval_acc = 0
    # 测试集不训练
    for img , label in test_data:
        img = img.reshape(img.size(0),-1)
        img = Variable(img)
        label = Variable(label)
        
        out = net(img)
        
        loss = criterion(out,label)
        
        # 记录误差
        eval_loss += loss.item()
        
        _ , pred = out.max(1)
        num_correct = (pred==label).sum().item()
        acc = num_correct / img.shape[0]
        eval_acc += acc
    eval_losses.append(eval_loss / len(test_data))
    eval_acces.append(eval_acc / len(test_data))
    print('Epoch {} Train Loss {} Train  Accuracy {} Teat Loss {} Test Accuracy {}'.format(
        epoch+1, train_loss / len(train_data),train_acc / len(train_data), eval_loss / len(test_data), eval_acc / len(test_data)))
    

输出：

Epoch 1 Train Loss 0.4592200527940668 Train  Accuracy 0.8540111940298507 Teat Loss 0.19474682688147207 Test Accuracy 0.9397745253164557
Epoch 2 Train Loss 0.15851766427855757 Train  Accuracy 0.9513259594882729 Teat Loss 0.12005600000767014 Test Accuracy 0.9638053797468354
Epoch 3 Train Loss 0.11475954767959967 Train  Accuracy 0.9645522388059702 Teat Loss 0.0904244807654921 Test Accuracy 0.971815664556962
Epoch 4 Train Loss 0.08745556761588115 Train  Accuracy 0.9721315298507462 Teat Loss 0.082516247948891 Test Accuracy 0.9746835443037974
Epoch 5 Train Loss 0.07025120377159322 Train  Accuracy 0.9772621268656716 Teat Loss 0.08604731969535351 Test Accuracy 0.9727056962025317
Epoch 6 Train Loss 0.05930126050530848 Train  Accuracy 0.9808935234541578 Teat Loss 0.08420209442795831 Test Accuracy 0.9721123417721519
Epoch 7 Train Loss 0.05124543002768874 Train  Accuracy 0.9834754797441365 Teat Loss 0.08631095639135264 Test Accuracy 0.9732001582278481
Epoch 8 Train Loss 0.04208977160645701 Train  Accuracy 0.986273987206823 Teat Loss 0.10187279088776323 Test Accuracy 0.969442246835443
Epoch 9 Train Loss 0.03568428441056056 Train  Accuracy 0.9885394456289979 Teat Loss 0.07184304212090335 Test Accuracy 0.9770569620253164
Epoch 10 Train Loss 0.031014378220319494 Train  Accuracy 0.9900719616204691 Teat Loss 0.06579126743010327 Test Accuracy 0.9791337025316456
Epoch 11 Train Loss 0.02508823178025451 Train  Accuracy 0.9920375799573561 Teat Loss 0.06799504674876793 Test Accuracy 0.9801226265822784
Epoch 12 Train Loss 0.023241530943002655 Train  Accuracy 0.9920209221748401 Teat Loss 0.2710842944068622 Test Accuracy 0.9364121835443038
Epoch 13 Train Loss 0.020258964756245553 Train  Accuracy 0.9934868070362474 Teat Loss 0.07330781534974333 Test Accuracy 0.9788370253164557
Epoch 14 Train Loss 0.018026590387005288 Train  Accuracy 0.994119802771855 Teat Loss 0.09561694470010226 Test Accuracy 0.9751780063291139
Epoch 15 Train Loss 0.01984227079747201 Train  Accuracy 0.9934701492537313 Teat Loss 0.06697431777285624 Test Accuracy 0.9814082278481012
Epoch 16 Train Loss 0.011230442394961172 Train  Accuracy 0.9962353411513859 Teat Loss 0.07196543846703783 Test Accuracy 0.9806170886075949
Epoch 17 Train Loss 0.012429191641557192 Train  Accuracy 0.9959521588486141 Teat Loss 0.1388555477031424 Test Accuracy 0.968057753164557
Epoch 18 Train Loss 0.014077426277911231 Train  Accuracy 0.9952691897654584 Teat Loss 0.07612939190732528 Test Accuracy 0.9816060126582279
Epoch 19 Train Loss 0.00572546272040176 Train  Accuracy 0.9985507729211087 Teat Loss 0.08512433384887025 Test Accuracy 0.9785403481012658
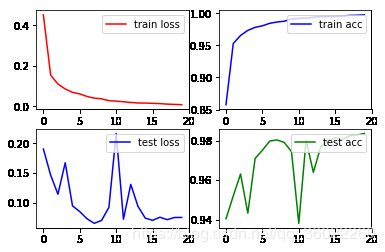
Epoch 20 Train Loss 0.00924977514821329 Train  Accuracy 0.9972181503198294 Teat Loss 0.07306018092115468 Test Accuracy 0.982001582278481

画出 loss 曲线和 准确率曲线

import matplotlib.pyplot as plt
%matplotlib inline
fig = plt.figure()

ax1 = plt.subplot(221)
ax1.plot(np.arange(len(losses)),losses,'r',label='train loss')
ax1.legend(loc='upper right')

ax2 = plt.subplot(222)
ax2.plot(np.arange(len(acces)),acces,'b',label='train acc')
ax2.legend(loc='upper right')

ax3 = plt.subplot(223)
ax3.plot(np.arange(len(eval_losses)),eval_losses,'b',label='test loss')
ax3.legend(loc='upper right')

ax4 = plt.subplot(224)
ax4.plot(np.arange(len(eval_acces)),eval_acces,'g',label='test acc')
ax4.legend(loc='upper right')
plt.show()

可以看出训练集正确率是99% 测试集可以达到98%。PS:（数据是由PyTorch内置包mnist中的数据）