HandsOn-ML学习笔记（1）用机器学习方法解决简单回归问题

很久没法博客了，可能自己也变懒了，正好最近在看一本大神推荐的书，准备写写笔记，把自己不会的，解决了的记录下来。文中的中文全部来自作者蹩脚的翻译，还望理解

书名叫《Hands-On Machine Learning with Scikit-Learn & Tensorflow》，我用的是东南大学的影印版，封面大概是这个样子（图片来自京东）

第一章主要是讲了机器学习的基础知识，主要的几个分类（监督学习与无监督学习，基于实例和基于模型的学习，线上学习和批量学习等等）和一些机器学习过程中容易遇到的一些问题，包括过拟合、欠拟合、测试集和验证集的划分等等，比较基础，在此一笔带过

我们的正文从第二章开始吧。第二章用一个房价预测例子来描述了一个完整的机器学习项目过程
主要任务有以下：

1. 获取数据
2. 数据可视化，发现数据的内在关系
3. 数据前期处理以便于机器学习算法
4. 选择模型并训练
5. 结果展示及更多

Step by step！

获取数据

关于获取数据，书中提到了几个开源的数据社区：

• UC Irvine Machine Learning Repository
• Kaggle datesets
• Amazon’s AWS datasets

这些社区的数据全部来自于真实数据，对想要熟悉机器学习的人来说比较合适，可以拿来练手

在获取了数据集之后，我们需要解决两个问题：

• 我们的业务目标究竟是什么？
• 当前的解决方案是怎么样的？

第一个问题也许你该问问你的BOSS，或许我们的目标是给下游的系统提供输入，或者别的目的；第二个问题可以看看相似问题在现实中是怎么解决的，效率和损耗怎么样，给机器学习的效果提供一个参照（我们要超越的目标）

下面我们需要确定我们的模型表现的评价标准，主要有下面几种方式：

1. RMSE（又叫L2范数、欧几里得范数）：
   
   1m∑i=1m(h(xi)−yi)2−−−−−−−−−−−−−−−√
2. MAE（L1范数、曼哈顿范数）：
   
   1m∑i−1m|h(xi−yi|

其中，范数的级别越高，就越对较大数值的数据敏感，越忽略较小的数据。故RMSE（Root Mean Square Error）比MAE（Mean Absolute Error）对异常值更敏感，当异常值很少时，RMSE表现出色

好了，可以开始我们的代码工作了

#读取代码并检查基本信息

import pandas as pd
housing = pd.read_csv('housing.csv')
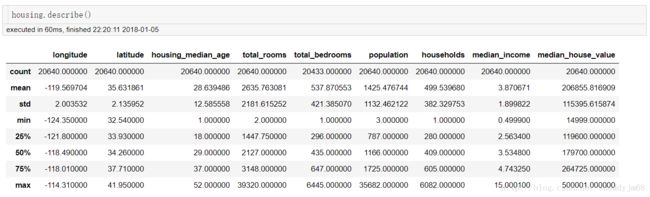
housing.info()#使用info查看各特征的基本信息

housing.describe()#使用describe查看数值型特征的数值特征

可以注意到ocean_proximity这个特征并不是数值型数据，这个我们会在数据预处理时单独处理

接下来看一下数值型数据的分布，用的是matplotlib

%matplorlib inline
import matplotlib.pyplot as plt
housing.hist(bins = 50, figsize = (15,12))#调整每个直方的宽度和图像的大小
plt.show()

从分布图中我们可以看出：

• housing_median_age 和 median_house_value 这两个特征有异常的数据，似乎是被数据采集人员截断了，我们后面可以选择删除错误数据或者给异常的数据添加新的标签
• 数据的范围不统一，后面为了模型更好地训练可能会使数据均一化
• 很多直方图的“尾巴”很长，我们可能要对这些数据进行处理使其更贴近钟型曲线（正态分布曲线）

接下来我们要划分数据集，将数据划分为训练集和测试集，最简单的方式是调用 sklearn.model_selection.train_test_split

from sklearn.model_selection import train_test_split

train_set, test_set = train_test_split(housing, test_size = 0.2\
                        ,random_state = 43)

当然，这种简单的划分方式并没有考虑到一些深层次的问题，如果数据集是分层抽样获取的，那么这样划分会打乱数据集原有的分层结构。下面我们新建一个特征，来帮助描述这个问题

#将收入除以1.5以避免收入跨度太大，再取上值
housing['income_cat'] = np.ceil(housing['median_income'] / 1.5)

#将income_cat中大于5的值全部转换成5
housing['income_cat'].where(housing['income_cat'] < 5, 5.0, inplace = True

from sklearn.model_selection import StratifiedShuffleSplit

split = StratifiedShuffleSplit(n_splits = 1, test_size = 0.2, random_state = 42)
for train_index, test_index in split.split(housing, housing['income_cat']):
    strat_train_set = housing.loc[train_index]
    strat_test_set = housing.loc[test_index]

使用 sklearn.model_selection.StratifiedShuffleSplit 就能轻松地实现分层的划分，划分后的数据集：

现在你可以把我们刚才新建的 income_cat 特征删掉，因为我们并不打算使用这个特征

for set in (strat_train_set, strat_test_set):
    set.drop(['income_cat'], axis = 1, inplace = True)

数据可视化

下面我们来看看数据可视化能帮助我们发现什么有用的信息

housing = strat_train_set.copy()
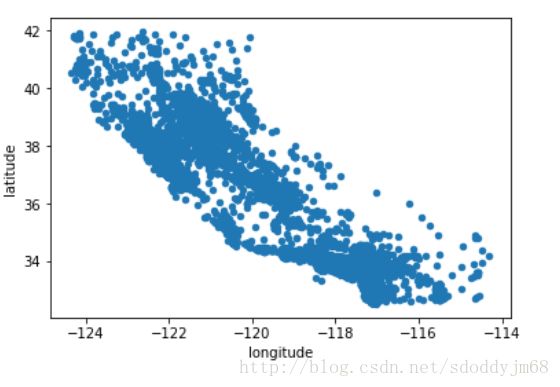
housing.plot(kind = 'scatter', x = 'longitude', y = 'latitude')

有些地方过于密集，不方便观察，调整一下透明度
housing.plot(kind = 'scatter', x = 'longitude', y = 'latitude', aplha = 0.1)
这样就能看出最密集的地区了

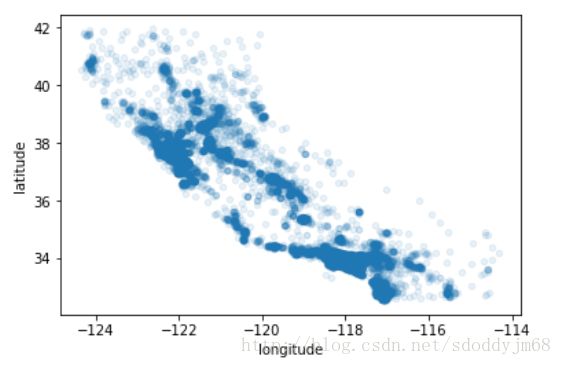
再加上一点点美化

housing.plot(kind = 'scatter', x = 'longitude', y = 'latitude', 
            alpha = 0.4,
            s = housing['population'] / 100, label = 'population',
            c = 'median_house_value', cmap = 'jet', colorbar = True)
plt.legend()

差不多就这个样子了，点的大小表示了人口的毕竟程度，颜色表示房价高低，可以看出在西边的地区人口密集程度很大，房价很高，东边人口很稀疏。看来地区的不同对房价确实是有影响的

下面我们看一下特征之间的相关程度，计算的方法是Pearson 方法，这种方法能检验特征之间是否存在正负线性关系

from pandas.tools.plotting import scatter_matrix

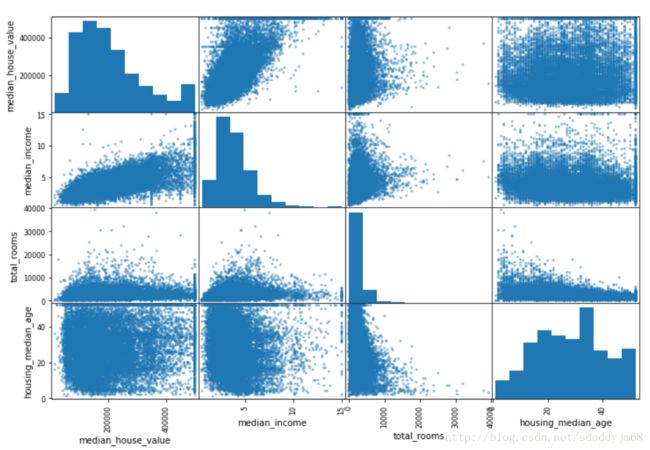
attributes = ['median_house_value', 'median_income', 'total_rooms', 'housing_median_age']
scatter_matrix(housing[attributes], figsize = (12,8))

画出来大概就是这样了，斜对角线画的直方图因为自己对自己的相关性肯定是1是一条直线没什么用。从图中可以看出，或许median_value这个特征和我们的目标特征关系密切，可以关注一下

除此之外，我们尝试加入三个新特征

housing['rooms_per_household'] = housing['total_rooms'] / housing['house_holds']
housing['bedrooms_per_room'] = housing['total_bedrooms'] / housing['total_rooms']
housing['population_per_household'] = housing['population'] / housing['households']

看看我们添加的特征有没有什么作用呢：

新添加的特征有一个甚至在与目标特征的相关性排名中拍到了第三，不错不错

下面我们要开始调整数据集以便模型的训练

#将标签分离出来
housing = strat_train_set.drop('median_house_value', axis = 1)
housing_labels = strat_train_set['median_house_value']

从之前info我们可以知道，部分特征是有缺失值的，对付缺失值我们有三个办法：

• 删掉该条样本
• 删掉整条特征
• 填充缺失值（0，平均值，中值等等）、

在sklearn中，我们可以使用sklearn.preprocessing.Imputer 来完成这一项任务

from sklearn.preprocessing import Imputer

imputer = Imputer(strategy = 'median')
housing_num = housing.drop('ocean_proximity', axis = 1)
X = imputer.fit_transform(housing_num)

终于要处理之前说到的ocean_proximity特征了，对于非数值型数据，我们一般转化为分类型数据（one-hot数组）

from sklearn.preprocessing import LabelBinarizer

housing_cat = housing['ocean_proximity']
encoder = LabelBinarizer()
housing_cat_1hot = encoder.fit_transform(housing_cat)

对与特征内部数据跨度太大的问题，我们可以进行Feature Scaling，主要使用的方法有两种：min-max scaling 和 standardization 。Min-max Scaling（也被称为normalization），通常把数据调整到0-1的范围内。Standardization一般不会把数据调整到具体的范围。两种调整方式中，Min-max对异常值非常敏感，比如大量数据处于0-15，有一个异常值100，经过Min-max处理之后所有数据就会在0-0.15的范围内，而Standardization在这方面就健壮地多

from sklearn.preprocssing import StandardScaler

std = StandardScaler()
housing_prepared = std.fit_transform(housing_num)
#合并两个数据
housing_prepared = np.concatenate([housing_prepared, housing_cat_1hot], axis = 1)

选择模型并训练

在这里我们选用的模型是随机森林回归，使用交叉验证的方式来对模型的性能做微小提升，关于交叉验证可以百度，这里使用的交叉验证方法是KFold验证，

from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_score

def  display_scores(scores):
    print('Scores: ', scores)
    print('Mean: ', scores.mean())
    print('Standard deviation: ', scores.std())

forest_reg = RandomForestRegressor()
scores = cross_val_score(forest_reg, housing_prepared, housing_labels, scoring = 'neg_mean_squared_error', cv = 10)

rmse_scores = np.sqrt(-scores)

display_scores(rmse_scores)

emmmmm，这个表现只能说也不算太坏

下面开始微调一下模型的参数，使用的方法是网格搜索，原理很简单，对每个参数组合进行训练，得分最高的模型就是最好的模型，在sklearn中我们可以用sklearn.model_selection.GridSearchCV ，而且找出最优参数之后，这个函数会帮你再fit一遍，省时省力

from sklearn.model_selection import GridSearchCV

#不同的花括号表示不同的批次
param_grid = [
    {'n_estimators': [8,16,32,64,128], 'max_features': [2,4,6,8,10]},
    {'bootstrap': [False], 'n_estimators': [10,50,100], 'max_features': [2,3,4]}
]

forest_reg = RandomForestRegressor()
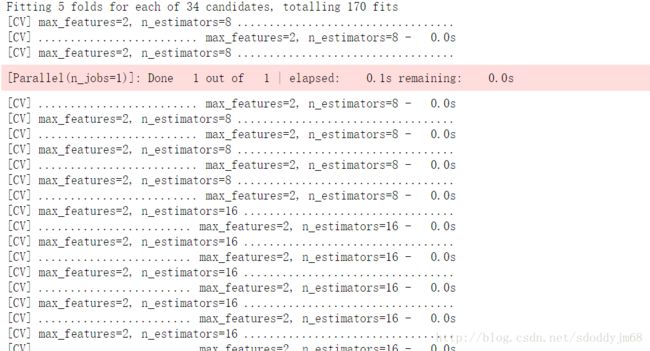
grid_search = GridSearchCV(forest_reg, param_grid, cv = 5, scoring = 'neg_mean_squared_error', verbose = 2)

grid_search.fit(housing_prepared, housing_labels)

搜索进行中：

跑个9分钟左右，输入grid_search.best_estimator_ 就能查看分析出来的最佳参数组合了

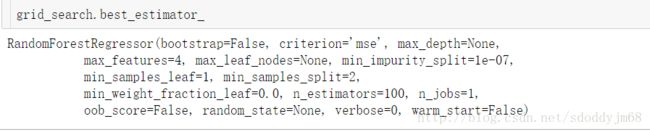
进行预测：

from sklearn.metrics import mean_squared_error
final_model = grid_search.best_estimator_
X_test = strat_test.drop('median_house_value', axis = 1)
y_test = strat_test['median_house_value']

X_test_cat = X_test['ocean_proximity']
X_test_cat_1hot = encoder.fit_transform(X_test_cat)

X_test_num = X_test.drop('ocean_proximity', axis = 1)
X_test_num = imputer.fit_transform(X_test_num)
X_test_num = std.fit_transform(X_test_num)

X_test = np.concatenate([X_test_num, X_test_cat_1hot], axis = 1)

final_predictions = final_model.predict(X_test)
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
print(final_rmse)

我的最后结果是47286.8，差不多都在这个数值左右吧

那这期就到这了，下一期尽量早点更新，这一次下定决定坚持写博客了