数学建模workflow
本人原创,转载请注明出处:https://blog.csdn.net/tyhj_sf/article/details/85227117
0. 引言
数学建模过程是一个创造性地将数学知识直接运用于生产实践以解决工程实际中的问题的工作过程。
不知道同学们有没有发现,理工科专业越往深入学发现涉及数学知识就越多,比如自动化、力学、计算机、管理科学等等,由专业背景知识抽象出的模型都是一堆的公式,此时数学知识就派上了用场。
个人认为每个理工科人都应该熟练掌握数学建模的方法,要具有数学建模的思维并将其用于解决实际工程问题的能力。
从本文开始我们将陆续用一些篇幅系统地总结数学建模的方法与技术,欢迎持续关注。
1. 数学建模与运筹优化
运筹学与数学建模是啥关系呢?
运筹学致力于运用数学建模的方法解决管理学和经济学中的实际问题,数学建模是运筹学中最基本的工作。
一般运筹学模型可以用一下格式数学形式描述:
max 或者 min 目标函数,
s.t. 约束条件
满足所有约束条件的解是可行解,同时使目标函数取值最佳的解称为最优解。
由于生活中的大部分问题都可以用如上形式描述,即优化类问题,这恰是数学建模要解决的问题之一,所以运筹学与数学建模有时候并没有明确的区分,可以说运筹学就是一个数学建模的过程。
需要搞清的是,数学建模不仅仅涵盖了运筹学,其涉及的面更广。
数学建模是根据现实对象的信息建立数学模型,并用数学方法求解,得到模型的解用来解释或验证现实的现象。
2. 数学建模的完整步骤
数学建模是一个从提出问题到解决问题的过程,完整的建模过程一般可以分为如7步:
第1步 根据需求提出问题并用数学语言描述
实际工业应用中的问题往往比较复杂,涉及领域背景知识比较多且约束条件多,问题的描述一般都是文字性的,读懂问题可能都不那么容易。因此来说,对于要解决的问题,首先就是用数学语言重新表达清楚,可以分以下几个小步骤解决:
(1)如果问题的背景知识不了解,需要先查阅文献了解领域相关知识;
(2)如果问题描述看不懂,就多阅读几遍直到看懂意思为止;
(3)列出问题中涉及到的所有变量包括适当的单位,用数学符号表示出来,注意区分出变量和常量;
(4)列出整个问题描述的假设以及我们已知的假设(即约束条件),当然是用数学语言描述,比如等式、不等式;
(5)用准确的数学语言写出整个问题想求解的目标的表达式,即目标函数;
第2步 选择建模方法
有了第1步对问题的数学描述后,我们需要选择一个或多个数学方法来获得问题的解,我们可以称这个解决方法为算法。要选择一个合适的方法求解问题,需要识别出问题的类型、理解各种类型问题的算法及其优缺点,还需要一些技巧及对相关文献有一定了解,这对问题解决者的能力要求较高,需要不断地训练和经验积累。
第3步 推导模型的公式
在第2步确定了解决算法后,需要对问题的数学描述进行变形、推导转化成算法要求的标准形式,注意记下任何补充假设,这些假设是为了使第1步中描述的问题与第2步选择的算法的数学结构标准形式相适应而做出的。
第4步 求解模型
求解模型有很多工具可以利用:
统计与数据分析:SPSS,、Eviews、SAS、Python、R等;
微分方程:MATLAB、Mathematics等;
运筹优化:Lingo、cplex、gurobi等;
时序预测和智能算法:R、Python等;
图像处理:MATLAB、C++等;
以上比较推荐还是用Python语言,它工具库及其丰富、编程简洁灵活,当前在数据分析、机器学习等领域被广泛使用。
第5步 验证模型
收集实际数据检验模型的合理性。检查一个模型是否正确的一般方法是:把模型的输出结果与历史输出数据进行比较,如果在相似的输入条件下,模型合理地重现了过去的情形,则这个模型就是合理的。对于没有历史数据的情况,我们可以模拟系统的运作来检验数学模型的输出结果的正确性。
第6步 实施模型
实施是把经过正确性检验的模型的解转换成能让人明白的操作指令,下达给系统执行。
这一步需要关注模型对用户友好。一个好的模型必须是数据输入方便,结果的输出具备可解释性,能够使用户或者决策者明白模型是否对他们有用。
第7步 维护模型
模型也是有有效期的,有些问题可能会随时间发生变化,某些先前忽略的因素会变得重要起来,原有的模型将不再有效,这就需要我们重新定义问题根据变化调整模型。
注意:
以上7步中,应重点关注第1步的数学语言描述问题和第4步的求解模型,这是两大难点,第一步中问题的数学定义的好坏直接影响后续算法的选择,第4步的模型求解关系到解的优劣、求解速度等重要问题。
3. 建模案例
以一个线性规划问题的数学建模为例:
需求:
某机床厂生产甲、乙两种机床,每台销售后的利润分别为4000 元与3000 元。
生产甲机床需用 A、B机器加工,加工时间分别为每台 2 小时和 1 小时;生产乙机床
需用 A、B、C三种机器加工,加工时间为每台各一小时。若每天可用于加工的机器时
数分别为A 机器10 小时、B 机器8 小时和C 机器7 小时,问该厂应生产甲、乙机床各
几台,才能使总利润最大?
第一步:将需求用数学语言描述
(1)首先问题定义出数学变量(包括自变量和因变量)
x 1 x_1 x1, 为该厂生产甲机床的数量;
x 2 x_2 x2, 为该厂生产乙机床的数量;
z z z, 为该厂生产的甲乙机床的总利润;
(2)列出约束条件的数学描述
约束条件1:A机器的每天工作时间不能超时,生产甲机床每台需用 A机器2个小时,生产已机床每台需用 A机器1个小时,每天可使用A机器的时间为10小时
数学描述: 2 x 1 + x 2 ≤ 10 2x_1 + x_2 \leq 10 2x1+x2≤10
约束条件2:B机器的每天工作时间不能超时,生产甲机床每台需用 B机器1个小时,生产乙机床需用 B机器1小时,每天可使用B机器的时间为8小时
数学描述: x 1 + x 2 ≤ 8 x_1 + x_2 \leq 8 x1+x2≤8
约束条件3:C机器的每天工作时间不能超时,生产甲机床每台需用C机器0个小时,生产乙机床需用C机器1小时,每天可使用C机器的时间为7小时
数学描述: x 2 ≤ 7 x_2 \leq 7 x2≤7
约束条件4:每天生产的机器数量不能为负值
数学描述: x 1 ≥ 0 , x 2 ≥ 0 x_1 \geq 0,x_2 \geq 0 x1≥0,x2≥0
(3)列出目标函数
需求问题:问该厂应生产甲、乙机床各几台,才能使总利润最大?(甲机床利润为4000,乙机床利润为3000)
数学描述为: m a x z = 4 x 1 + 3 x 2 max\ z=4x_1+3x_2 max z=4x1+3x2等价于
m a x z = 4000 x 1 + 3000 x 2 max\ z=4000x_1+3000x_2 max z=4000x1+3000x2
最终,问题的数学模型如下:
m a x z = 4000 x 1 + 3000 x 2 max\ z=4000x_1+3000x_2 max z=4000x1+3000x2
s . t . s.t. s.t.
2 x 1 + x 2 ≤ 10 \ \ \ \ 2x_1 + x_2 \leq 10 2x1+x2≤10
x 1 + x 2 ≤ 8 \ \ \ \ x_1 + x_2 \leq 8 x1+x2≤8
x 2 ≤ 7 \ \ \ \ x_2 \leq 7 x2≤7
x 1 ≥ 0 , x 2 ≥ 0 \ \ \ \ x_1 \geq 0,x_2 \geq 0 x1≥0,x2≥0
第2步 选择建模方法
根据第1步建立的数学模型可以很容易看出,目标函数及其约束条件均为线性函数,故这是为线性规划问题,可以考虑用现有的求解器求解,比如OR-tools,后续文章将主要用此工具来讲解运筹优化问题案例求解。关于线性规划,我们将在后续文章中专门介绍,本节暂不细说。
第3步 推导模型的公式
我们建好的数学模型并不符合求解器规定的形式,需要做适当的等价变换、推导等操作:
(1)将目标函数由 m a x z = 4000 x 1 + 3000 x 2 max\ z=4000x_1+3000x_2 max z=4000x1+3000x2简化为 m i x z = − 4 x 1 − 3 x 2 mix\ z=-4x_1-3x_2 mix z=−4x1−3x2,其最优解并不会变化;
(2) x 1 ≥ 0 , x 2 ≥ 0 \ \ \ \ x_1 \geq 0,x_2 \geq 0 x1≥0,x2≥0改变为 − x 1 ≤ 0 , − x 2 ≤ 0 \ \ \ \ -x_1 \leq 0,-x_2 \leq 0 −x1≤0,−x2≤0
经过以上变换,满足某些求解器的以下标准形式:
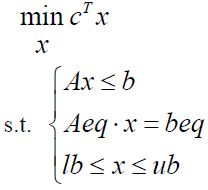
其中, c 和x 为n 维列向量, A 、Aeq 为适当维数的矩阵, b 、beq 为适当维数的列向
量。
最后,我们的数学模型就变成如下形式:
m i x z = − 4 x 1 − 3 x 2 mix\ z=-4x_1-3x_2 mix z=−4x1−3x2
s . t . s.t. s.t.
2 x 1 + x 2 ≤ 10 \ \ \ \ 2x_1 + x_2 \leq 10 2x1+x2≤10
x 1 + x 2 ≤ 8 \ \ \ \ x_1 + x_2 \leq 8 x1+x2≤8
x 2 ≤ 7 \ \ \ \ x_2 \leq 7 x2≤7
− x 1 ≤ 0 , − x 2 ≤ 0 \ \ \ \ -x_1 \leq 0,-x_2 \leq 0 −x1≤0,−x2≤0
第4步 求解模型
一般都是借助计算机求解,使用工具OR-tools +python可以解决这种简单的线性规划问题,这部分将在后续文章中详细讲解。
第5步 验证模型
验证的话有时并不是那么容易,本案例可以将方案与历史数据做对比,就不细说了。
第6步 实施模型
经过求解器求解后,获得了最优方案中 x 1 , x 2 x_1,x_2 x1,x2的值,比如本案例,用在实际生产中就是根据这些值为人员和机器安排生产任务。
第7步 维护模型
模型在生产环境中使用时,会涉及到这一步,比如长期使用后,约束条件随时间发生了改变,数学模型也会随之改变,比如本案例中的机器加工时间发生改变,要及时的修正,这就是维护过程。
4. 建模方法
数学规划类的建模方法有:线性规划、整数规划、非线性规划等几种,可以用来对最优化问题建模并利用一些成熟工具求解,比如cplex、gurobi、lingo、OR-tools等。
多目标优化问题可以考虑用目标规划模型建模并求解。
序列决策问题可以考虑马尔科夫模型,可以用RL类算法来求解。
工程上的一些问题可以用微分方程建模。
时序数据可以根据维数建立单维、多维时间序列模型,如ARMA、ARIMA、Holter-Winter、RNN等算法模型可以使用。
预测问题、数据拟合问题可以用回归分析方法建模,这类问题可以采用SVM、神经网络、线性回归等算法来解决。
本节并不打算细讲各类模型的求解算法,一篇文章是讲不完的,我会在后续文章中针对每类问题逐个讲解。
5. 参考资料
[1].《运筹学导论》第9版,希利尔;
[2].《数学建模》第五版;