深度学习（07）_RNN-循环神经网络-02-Tensorflow中的实现

• 关于基本的RNN和LSTM的概念和BPTT算法可以查看这里
• 本文个人博客地址：点击这里
• 参考文章：
  
  • https://r2rt.com/recurrent-neural-networks-in-tensorflow-i.html
  • https://r2rt.com/styles-of-truncated-backpropagation.html

一、源代码实现一个binary例子

1、例子描述

(1) 数据描述

• 输入数据X是二进制的一串序列, 在t时刻，有50%的概率是1，50%的概率是0，比如：X=[1,1,0,0,1,0.....]

• 输出数据Y：
  
  • 在时刻t，50%的概率是1，50%的概率是0；
  • 如果 Xt−3 是1，则 Yt 100%是1（增加50%）；
  • 如果 Xt−8 是1，则 Yt 25%是1（减少25%）；
  • 所以如果 Xt−3 和 Xt−8 都是1，则 Yt 50%+50%-25%=75%的概率是1
• 所以，输出数据是有两个依赖关系的

(2) 损失函数

• 使用cross-entropy损失函数进行训练
• 这里例子很简单，根据数据生成的规则，我们可以简单的计算一下不同情况下的cross-entropy值
• [1] 如果rnn没有学到两个依赖关系, 则最终预测正确的概率是62.5%，cross entropy值为0.66计算如下
  
  • 
  • 所以正确预测1的概率为：(0.75+1+0.25+0.5)/4=0.625
  • 所以cross entropy值为：-[plog(p)+(1-p)log(1-p)]=0.66
• [2] 如果rnn学到第一个依赖关系，50%的情况下预测准确度为87.5%，50%的情况下预测准确度为62.5%，cross entropy值为0.52
  
  • 因为X是随机生成，0/1各占50%,想象生成了很多的数，根据大数定律，50%的情况是1，对应到 [1] 中的上面的情况就是:(0.75+1)/2=0.875的概率预测正确，其余的50%就和[1]中一样了（去除学到的一个依赖，其余就是没有学到依赖）62.5%
  • 损失值：-0.5 * (0.875 * .log(0.875) + 0.125 * log(0.125))-0.5 * (0.625 * np.log(0.625) + 0.375 * log(0.375)))=0.52
• [3] 如果rnn两个依赖都学到了，则25%的情况下100%预测正确，25%的情况下50%预测正确，50%的情况向75%预测正确，cross entropy值为0.45
  
  • 1/4的情况就是 Xt−3=1和Xt−8=0 100%预测正确
  • 1/4的情况就是 Xt−3=0和Xt−8=0 50%预测正确
  • 1/2的情况75%预测正确（0.5+0.5-0.25）
  • 损失值：-0.50 * (0.75 * np.log(0.75) + 0.25 * np.log(0.25)) - 0.25 * (2 * 0.50 * np.log (0.50)) - 0.25 * (0) = 0.45

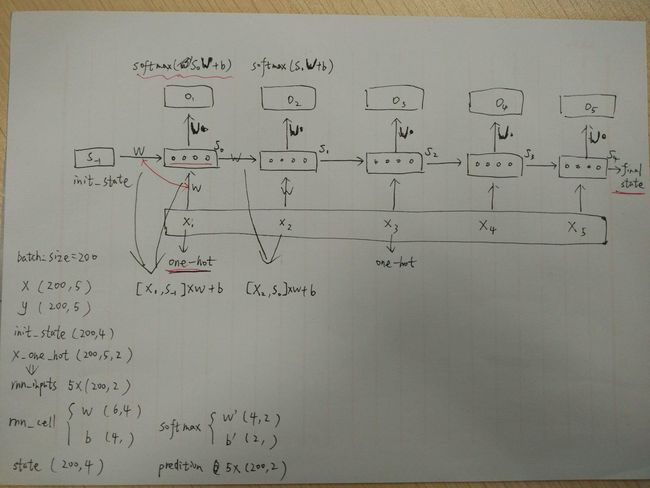
2、网络结构

• 根据时刻t的输入向量 Xt 和时刻t-1的状态向量state St−1 计算得出当前的状态向量 St 和输出的结果概率向量 Pt
• Label数据是Y

• 所以有：

  St=tanh(W(Xt⨁St−1))+bs
  Pt=softmax(USt+bp)
  • 这里 ⨁ 表示向量的拼接
  • W∈Rd×(2+d),bs∈Rd,U∈R2×d,bp∈R2
  • d是 state 向量的长度
  • W是二维的矩阵，因为是将 Xt和St−1 拼接起来和W运算的，2对应输入的X one-hot之后，所以是2

  • U是最后输出预测的权值

  • 初始化state S−1 为0向量

- 需要注意的是 cell 并不一定是只有一个neuron unit，而是有n个hidden units
- 下图的state size=4

3、Tensorflow中RNN BPTT实现方式

1) 截断反向传播（truncated backpropagation）

• 假设我们训练含有1000000个数据的序列，如果全部训练的话，整个的序列都feed进RNN中，容易造成梯度消失或爆炸的问题
• 所以解决的方法就是truncated backpropagation，我们将序列截断来进行训练(num_steps)

2) tensorflow中的BPTT算法实现

• 一般截断的反向传播是：在当前时间t,往前反向传播num_steps步即可
  
  • 如下图，长度为6的序列，截断步数是3

- 但是Tensorflow中的实现并不是这样(如下图)
- 它是将长度为6的序列分为了两部分，每一部分长度为3
- 前一部分计算得到的final state用于下一部分计算的initial state

- 所以tensorflow风格的反向传播并没有有效的反向传播num_steps步(对比一般的方式，依赖关系变的弱一些)
- 所以比如想要学习有8依赖关系的序列（我们的例子中就是），一般要设置的大于8
- 另外，有人做实验比较了两种方式here，发现一般的实现方式中的n步和Tensorflow中截断设置为2n的结果相似

3) 关于这个例子，tensorflow风格的实现

• 如下图，num_steps=5, state_size=4，就是**截断反向传播的步数**truncated backprop steps是5步，state_size就是cell中的神经元的个数
• 如果需要截断的步数增多，可以适当增加state_size来记录更多的信息
  
  • 好比传统的神经网络，就是增加隐藏层的神经元个数
• 途中的注释是下面的列子代码中定义变量的shape, 可以对照参考

4、自己实现例子中的RNN

• 全部代码：https://github.com/lawlite19/Blog-Back-Up/blob/master/code/rnn/rnn_implement.py

1) 实现过程

• 导入包：

import numpy as np
import tensorflow as tf
from tensorflow.python import debug as tf_debug
import matplotlib.pyplot as plt

• 超参数
  
  • 这里num_steps=5就是只能记忆5步, 所以只能学习到一个依赖(因为至少8步才能学到第二个依赖)，我们看结果最后的cross entropy是否在0.52左右

'''超参数'''
num_steps = 5
batch_size = 200
num_classes = 2
state_size = 4
learning_rate = 0.1

• 生成数据
  
  • 就是按照我们描述的规则

'''生成数据
就是按照文章中提到的规则，这里生成1000000个
'''
def gen_data(size=1000000):
    X = np.array(np.random.choice(2, size=(size,)))
    Y = []
    '''根据规则生成Y'''
    for i in range(size):   
        threshold = 0.5
        if X[i-3] == 1:
            threshold += 0.5
        if X[i-8] == 1:
            threshold -=0.25
        if np.random.rand() > threshold:
            Y.append(0)
        else:
            Y.append(1)
    return X, np.array(Y)

• 生成batch数据，因为我们使用sgd训练

'''生成batch数据'''
def gen_batch(raw_data, batch_size, num_step):
    raw_x, raw_y = raw_data
    data_length = len(raw_x)
    batch_patition_length = data_length // batch_size                         # ->5000
    data_x = np.zeros([batch_size, batch_patition_length], dtype=np.int32)    # ->(200, 5000)
    data_y = np.zeros([batch_size, batch_patition_length], dtype=np.int32)    # ->(200, 5000)
    '''填到矩阵的对应位置'''
    for i in range(batch_size):
        data_x[i] = raw_x[batch_patition_length*i:batch_patition_length*(i+1)]# 每一行取batch_patition_length个数，即5000
        data_y[i] = raw_y[batch_patition_length*i:batch_patition_length*(i+1)]
    epoch_size = batch_patition_length // num_steps                           # ->5000/5=1000 就是每一轮的大小
    for i in range(epoch_size):   # 抽取 epoch_size 个数据
        x = data_x[:, i * num_steps:(i + 1) * num_steps]                      # ->(200, 5)
        y = data_y[:, i * num_steps:(i + 1) * num_steps]
        yield (x, y)    # yield 是生成器，生成器函数在生成值后会自动挂起并暂停他们的执行和状态（最后就是for循环结束后的结果，共有1000个(x, y)）
def gen_epochs(n, num_steps):
    for i in range(n):
        yield gen_batch(gen_data(), batch_size, num_steps)

• 定义RNN的输入
  
  • 这里每个数需要one-hot处理
  • unstack方法就是将n维的数据拆成若开个n-1的数据，axis指定根据哪个维度拆的，比如(200,5,2)三维数据，按axis=1会有5个(200,2)的二维数据

'''定义placeholder'''
x = tf.placeholder(tf.int32, [batch_size, num_steps], name="x")
y = tf.placeholder(tf.int32, [batch_size, num_steps], name='y')
init_state = tf.zeros([batch_size, state_size])
'''RNN输入'''
x_one_hot = tf.one_hot(x, num_classes)
rnn_inputs = tf.unstack(x_one_hot, axis=1)

• 定义RNN的cell（关键步骤）
  
  • 这里关于name_scope和variable_scope的用法可以查看这里

'''定义RNN cell'''
with tf.variable_scope('rnn_cell'):
    W = tf.get_variable('W', [num_classes + state_size, state_size])
    b = tf.get_variable('b', [state_size], initializer=tf.constant_initializer(0.0))

def rnn_cell(rnn_input, state):
    with tf.variable_scope('rnn_cell', reuse=True):
        W = tf.get_variable('W', [num_classes+state_size, state_size])
        b = tf.get_variable('b', [state_size], initializer=tf.constant_initializer(0.0))
    return tf.tanh(tf.matmul(tf.concat([rnn_input, state],1),W) + b)

• 将cell添加到计算图中

'''将rnn cell添加到计算图中'''
state = init_state
rnn_outputs = []
for rnn_input in rnn_inputs:
    state = rnn_cell(rnn_input, state)  # state会重复使用，循环
    rnn_outputs.append(state)
final_state = rnn_outputs[-1]        # 得到最后的state

• 定义预测，损失函数，和优化方法
  
  • sparse_softmax_cross_entropy_with_logits会自动one-hot

'''预测，损失，优化'''
with tf.variable_scope('softmax'):
    W = tf.get_variable('W', [state_size, num_classes])
    b = tf.get_variable('b', [num_classes], initializer=tf.constant_initializer(0.0))
logits = [tf.matmul(rnn_output, W) + b for rnn_output in rnn_outputs]
predictions = [tf.nn.softmax(logit) for logit in logits]

y_as_list = tf.unstack(y, num=num_steps, axis=1)
losses = [tf.nn.sparse_softmax_cross_entropy_with_logits(labels=label,logits=logit) for logit, label in zip(logits, y_as_list)]
total_loss = tf.reduce_mean(losses)
train_step = tf.train.AdagradOptimizer(learning_rate).minimize(total_loss)

• 训练网络

'''训练网络'''
def train_rnn(num_epochs, num_steps, state_size=4, verbose=True):
    with tf.Session() as sess:
        sess.run(tf.global_variables_initializer())
        #sess = tf_debug.LocalCLIDebugWrapperSession(sess)
        training_losses = []
        for idx, epoch in enumerate(gen_epochs(num_epochs, num_steps)):
            training_loss = 0
            training_state = np.zeros((batch_size, state_size))   # ->(200, 4)
            if verbose:
                print('\nepoch', idx)
            for step, (X, Y) in enumerate(epoch):
                tr_losses, training_loss_, training_state, _ = \
                    sess.run([losses, total_loss, final_state, train_step], feed_dict={x:X, y:Y, init_state:training_state})
                training_loss += training_loss_
                if step % 100 == 0 and step > 0:
                    if verbose:
                        print('第 {0} 步的平均损失 {1}'.format(step, training_loss/100))
                    training_losses.append(training_loss/100)
                    training_loss = 0
    return training_losses

• 显示结果

training_losses = train_rnn(num_epochs=1, num_steps=num_steps, state_size=state_size)
print(training_losses[0])
plt.plot(training_losses)
plt.show()

2) 实验结果

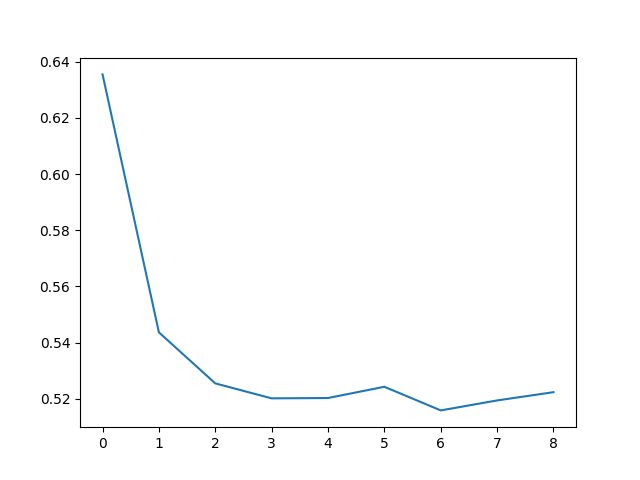
• num_steps=5, state=4
  
  • 可以看到初试的损失值大约0.66, 最后学到一个依赖关系，最终损失值0.52左右

- num_step=10, state=16
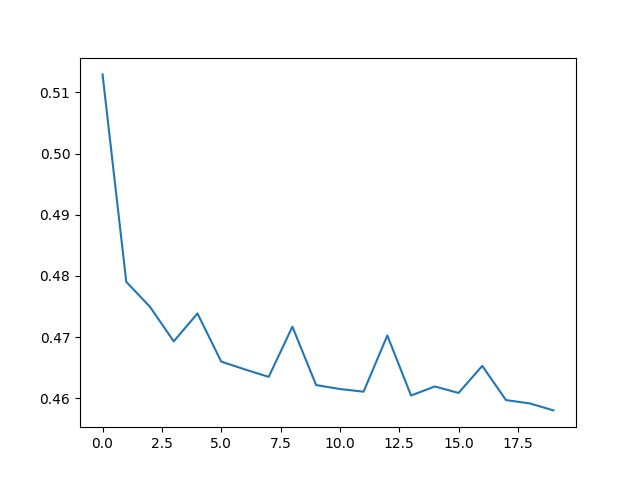
- 学到了两个依赖，最终损失值接近0.45

5、使用Tensorflow的cell实现

1) 使用static rnn方式

• 将我们之前自己实现的cell和添加到计算图中步骤改为如下即可

cell = tf.contrib.rnn.BasicRNNCell(num_units=state_size)
rnn_outputs, final_state = tf.contrib.rnn.static_rnn(cell=cell, inputs=rnn_inputs, 
                                                    initial_state=init_state)

2) 使用dynamic_rnn方式

• 这里仅仅替换cell就不行了，RNN输入
  
  • 直接就是三维的形式

'''RNN输入'''
rnn_inputs = tf.one_hot(x, num_classes)

• 使用dynamic_rnn

cell = tf.contrib.rnn.BasicRNNCell(num_units=state_size)
rnn_outputs, final_state = tf.nn.dynamic_rnn(cell, rnn_inputs, initial_state=init_state)

• 预测，损失
  
  • 由于rnn_inputs是三维的，所以先转成二维的，计算结束后再转换回三维[batch_size, num_steps, num_classes]

    '''因为rnn_outputs是三维的，这里需要将其转成2维的，
       矩阵运算后再转换回来[batch_size, num_steps, num_classes]'''
logits = tf.reshape(tf.matmul(tf.reshape(rnn_outputs, [-1, state_size]), W) +b, \
                    shape=[batch_size, num_steps, num_classes])
predictions = tf.nn.softmax(logits)

y_as_list = tf.unstack(y, num=num_steps, axis=1)
losses = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,logits=logits)
total_loss = tf.reduce_mean(losses)
train_step = tf.train.AdagradOptimizer(learning_rate).minimize(total_loss)

Reference

• https://r2rt.com/recurrent-neural-networks-in-tensorflow-i.html
• https://r2rt.com/styles-of-truncated-backpropagation.html
• https://web.stanford.edu/class/psych209a/ReadingsByDate/02_25/Williams%20Zipser95RecNets.pdf