深度学习入门（一）感知机与激活函数

25天看完了吴恩达的机器学习以及《深度学习入门》和《tensorflow实战》两本书，吴恩达的学习课程只学了理论知识，另外两本书的代码自己敲了一遍，感觉过的太快，趁着跑cGAN的时间把两本书的知识点总结下，然后继续深度学习的课程。欢迎小伙伴一起学习~
另外，本文先把框架搭好，后续会一直补充细节和知识点。
最后，本文参考的书是《深度学习入门》斋藤康毅著，十分推荐初学者使用。

本文的代码地址

感知机

神经网络最早起源于感知机，感知机有与门、非门、或门和异或门。
输入为1或0，输出也是1或零

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    elif tmp > 0:
        return 1

通过调整w的权重可以分别实现与门、或门和非门这里不再赘述，这里我们看下异或门，异或门是指输入相同时为0，输入不同时为1，感知机的局限表现在不能表示异或门，但是可以通过叠加层来实现,通过与非门和或门后再通过与门最后结果就是我们想要d额异或门啦

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

激活函数

上面我们提到感知机有个局限性，无法单层表示非线性变化，而神经网络通过激活函数用来表示非线性变化。
关于激活函数，本文的分享以代码为主，理论建议参考激活函数链接，对于当前的各个激活函数介绍比较详细。

1.sigmoid

$$sig(x)=\frac{1}{1+e^{-x}}$$
sigmoid导数$=(1-sig)\ast sig$
下面代码实际是一个类，类的forward函数就是sigmoid激活函数，backward函数就是反向传播求梯度的过程

class Sigmoid:
    def __init__(self):
        self.out = None
    def forward(self, x):
        out = sigmoid(x)
        self.out = out
        return out
    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out
        return dx

2.tanh

$$tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$$
tanh导数$=1-{tanh(x)}^2$

与sigmoid相比，它的输出均值是0，使得其收敛速度要比sigmoid快，减少迭代次数。目前接触到常见有循环网络计算隐藏状态和cycleGAN的生成器中的解码器最后一层使用的tanh激活函数。

3.relu

$$f(x)=\{\begin{array}{rlr}0& & x<=0\\ x& & x>0\end{array}$$
$$即f(x)=max(x,0)$$
relu 作为激活函数，梯度收敛快，且梯度计算量相对较少。

def sigmoid(x):
    return 1 / (1 + np.exp(-x))
class Relu:
    def __init__(self):
        self.mask = None
    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0
        return out
    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        return dx

4.softmax

softmax输出的是上一层的值指数计算后分别所占比例，为了避免指数函数变得过大，我们采用减去最大值的方式，并不改变最终结果。
$$x_j=\frac{e^{x_j-x_{max}}}{{\sum }_{i=1}^n{e}^{x_i-x_{max}}}$$
softmax分类器用于分类器有比较神奇的作用，我们只考虑一个全连接层神经网络，不含隐藏层，假设输入特征为$x_1,x_2$，只通过全连接层$z^{[1]}=W^{[1]}x+b^{[1]}$，然后应用softamx函数，它可以利用线性函数把空间分为多个类。


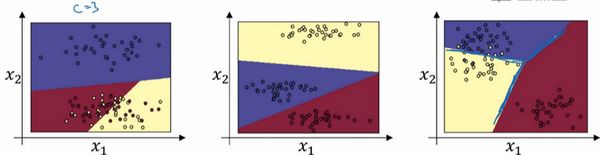
注意：当分类个数C为2时，就变为logistic回归
softmax的损失通过$-{\sum }_j^C{y}_j\log y_j^{\ast }$，由于y只有一个值为1时计算才不为0，这就转化为在y不等于1对应的预测的概率大小，然后转化为最大似然估计，即在确定分布的情况下，求得是该概率最大的参数的取值。
有时间再来推到下softmax反向传播的的计算…

softmax通常和计算loss在一起，这里我们构建了一softmax_with_loss
类

def softmax(a):
	c = np.max(a)
	exp_a = np.exp(a-c)
	exp_sum = np.sum(exp_a)
	return exp_a / exp_sum
class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None
        self.t = None
    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        return self.loss
    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size: # if t is one-hot-vector
            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size
        return dx

softmax参考吴恩达深度学习 第三周 超参数调试、Batch正则化和程序框架