# 莫队算法及各种变体(持续更新)

莫队算法及各种变体(持续更新)

简单介绍

博客安利：

1. OI Wiki
2. 大米饼

解决一类离线区间查询问题，分块思想，时间复杂度\(O(n\sqrt n)\)

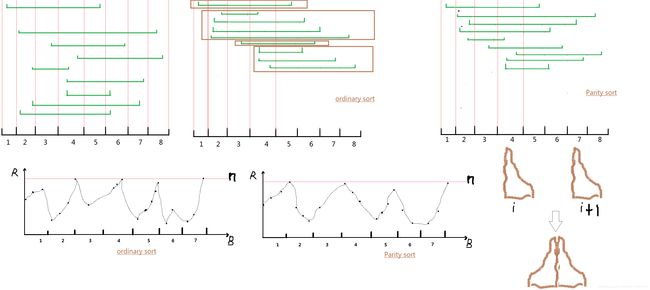
• 排序

  读入的时候对整个数组进行分块，块大小一般使用\(\sqrt n\)，对询问操作排序的时候，先以块号为第一关键字，\(r\)为第二关键字，从小到大排序，然后逐个遍历

  离线后将询问排序，顺序处理每个询问，暴力从上一个区间的答案转移到下一个区间的答案（通过两个指针的\(++\)和\(--\)操作实现）

• 指针移动

  

  当\(l\)指针从绿色区域向右移动一格，更新操作对应，先减去cnt[绿色]的共享，cnt[绿色]\(--\)，再加上cnt[绿色]区域的贡献，其他指针移动操作类似。

基础莫队

• 题目链接：

  给出n只袜子颜色，每次给个区间\([l,r]\)，询问这个区间连续取两只袜子取到同一种颜色的概率。

• 思路：

  对于L,R的询问。

  设其中颜色为x,y,z的袜子的个数为a,b,c..…

  那么答案即为 \((a*(a-1)/2+b*(b-1)/2+c*(c-1)/2....)/((R-L+1)*(R-L)/2)\)

  化简得: \((a^2+b^2+c^2+...x^2-(a+b+c+d+.....))/((R-L+1)*(R-L))\)

  即： \((a^2+b^2+c^2+...x^2-(R-L+1))/((R-L+1)*(R-L))\)

  我们需要解决的一个问题是：求一个区间内每种颜色数目的平方和。

• AcCode：

#include 
#include 
#include 
using namespace std;
typedef long long LL;
const int maxn=5e4+5;
//存储询问区间
struct node{int l,r,id;LL A,B;}q[maxn];
//in[]存储每个数所在的区间
int n,m,a[maxn],in[maxn];
//处理前预排序
inline bool cmp(node& a,node& b){
    return in[a.l]==in[b.l]?a.rq[i].l)update(l-1,1),l--;
        while(rq[i].r)update(r,-1),r--;

        if(l==r){q[i].A=0,q[i].B=1;continue;}
        q[i].A=ans-(r-l+1);
        q[i].B=1LL*(r-l+1)*(r-l);
        LL gc=__gcd(q[i].A,q[i].B);
        q[i].A/=gc,q[i].B/=gc;
    }
}
int main(){
    cin>>n>>m;
    int sqr=sqrt(n);
    for(int i=1;i<=n;++i)cin>>a[i],in[i]=i/sqr+1;
    for(int i=1;i<=m;++i)cin>>q[i].l>>q[i].r,q[i].id=i;
    
    sort(q+1,q+1+m,cmp);
    
    solve();
    
    sort(q+1,q+1+m,CMP);
    
    for(int i=1;i<=m;++i)
        printf("%lld/%lld\n",q[i].A,q[i].B);
    return 0;
}

奇偶排序优化

博客安利： https://oi-wiki.org/misc/mo-algo/ ， https://www.cnblogs.com/WAMonster/p/10118934.html

奇数块中r从小到大排序，偶数块中r从大到小排序（第一块的快数为1，且初始\(l=1,r=0\)，在\(r\)指针从小到大向右跳的时候，正好处理完第一块的询问，此时\(r\)位于第一块中\(r\)最大值的地方，接下来处理偶数块，即第二块，偶数块中\(r\)为从大到小排序，第二块中的第一个询问正好是第二块中的\(r\)的最大值）。

主要原理便是右指针 跳完奇数块往回跳时在同一个方向能顺路把偶数块跳完，然后跳完这个偶数块又能顺带把下一个奇数块跳完。理论上主算法运行时间减半，实际情况有所偏差。

这种优化能让程序快30%左右，据说每个点平均优化200ms

inline bool cmp(node& a, node& b) {
    return (belong[a.l] ^ belong[b.l]) ? belong[a.l] < belong[b.l] : ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r);
}

指针移动的常数优化

运用运算符优先级知识，把

void add(int pos) {
    if(!cnt[aa[pos]]) ++now;
    ++cnt[aa[pos]];
}
void del(int pos) {
    --cnt[aa[pos]];
    if(!cnt[aa[pos]]) --now;
}

和这个

while(l < ql) del(l++);
while(l > ql) add(--l);
while(r < qr) add(++r);
while(r > qr) del(r--);

硬生生压缩成这个：

while(l < ql) now -= !--cnt[aa[l++]];
while(l > ql) now += !cnt[aa[--l]]++;
while(r < qr) now += !cnt[aa[++r]]++;
while(r > qr) now -= !--cnt[aa[r--]];

但是并不是每一次莫队的使用都能这样压缩，视实际情况而定。

带修莫队

类比普通莫队，引入第三关键字“修改时间”， 表示当前询问是发生在前Time个修改操作后的。也就是说，在进行莫队算法时，看看当前的询问和时间指针（第三个指针，别忘了l,r）是否相符，然后进行时光倒流或者时光推移操作来保证答案正确性。 \(O(unit*n+n2/unit+(n/unit)2*n)\) ,\(unit=n^{2/3}\)时，取最小为\(O(n^{5/3})\).

题目链接:

给定n个颜色，m条指令（含修改和查询）

1. \(Q\quad l\quad r\) 询问颜色种数
2. \(R\quad pos\quad y\) 将pos位置的颜色修改为\(y\)

RE代码：

//加减代替取模优化，多数组结构体优化，puts()输出优化，自带换行
#include 
using namespace std;
#define fre freopen("data.in","r",stdin);
#define frew freopen("sol.out","w",stdout);
#define ms(a) memset((a),0,sizeof(a))
#define go(i, a, b) for(register int i=(a);(i)<(b);++(i))
#define rgo(i, a, b) for(register int i=(a);(i)>(b);--(i))
#define re(i, a, b) for(register int i=(a);(i)<=(b);++(i))
#define rre(i, a, b) for(register int i=(a);(i)>=(b);--(i))
#define all(x) (x).begin(),(x).end()
#define pb push_back
#define lson l,m,i<<1
#define rson m+1,r,i<<1|1
#define reg register
typedef long long LL;
const int inf = (0x7f7f7f7f);

inline void sf(int &x) {
    x = 0;
    int w = 0;
    char ch = 0;
    while (!isdigit(ch)) {
        w |= ch == '-';
        ch = getchar();
    }
    while (isdigit(ch)) x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
    x = (w ? -x : x);
}

inline void pf(int x) {
    if (x < 0) putchar('-'), x = -x;
    if (x > 9) pf(x / 10);
    putchar(x % 10 + '0');
}

const int maxn = 10003;
struct query{
    int l,r,tim,id,bk,ans;
}q[maxn];
struct change{
    int pos,nw,od;
}c[maxn];
int now[maxn],a[maxn];
int n,m,T,t,tim;
char op;
int ans;
int cnt[maxn];
inline bool cmp(const query& a,const query& b){
    return a.bk==b.bk?(a.r==b.r?(a.timb.r)):a.l>op>>x>>y;
        scanf(" %c %d %d",&op,&x,&y);
        //cout<q[i].tim)solve(c[tim].pos,c[tim].od,l,r),tim--;

        while(lq[i].l)push(a[l-1],1),l++;
        while(rq[i].r)pop(a[r],1),r--;
        q[i].ans=ans;
    }
    sort(q+1,q+1+t,CMP);
    //cout<<"t :"<

树上莫队

树上带修莫队