ctf-实验吧-crypto
1.trivial
下载文件解压,得到一个py文件,里面又一个加密算法,这是一个类移位加密,加密算法的key和加密之后的密文已知,然后对每个明文在不同范围内进行移位加密,直接解密即可
#!/usr/bin/env python
import sys
alphaL = "abcdefghijklnmopqrstuvqxyz"
alphaU = "ABCDEFGHIJKLMNOPQRSTUVQXYZ"
num = "0123456789"
keychars = num+alphaL+alphaU
key="T0pS3cre7key"
plaintext="Bot kmws mikferuigmzf rmfrxrwqe abs perudsf! Nvm kda ut ab8bv_w4ue0_ab8v_DDU"
ciphertext=""
for i in range(len(plaintext)):
rotate_amount = keychars.index(key[i%len(key)])
if plaintext[i] in alphaL:
enc_char = ord('a') + (ord(plaintext[i])-ord('a')-rotate_amount)%26
elif plaintext[i] in alphaU:
enc_char = ord('A') + (ord(plaintext[i])-ord('A')-rotate_amount)%26
elif plaintext[i] in num:
enc_char = ord('0') + (ord(plaintext[i])-ord('0')-rotate_amount)%10
else:
enc_char = ord(plaintext[i])
ciphertext = ciphertext + chr(enc_char)
print ciphertext
2.rsarsa
rsa加密,已知p,q,e,c,算出n,d,直接解密,提交十进制的明文即可
import gmpy2
p=9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
q=11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
e=65537
c=83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034
n=p*q
d=int(gmpy2.invert(e,(p-1)*(q-1)))
mingwenint=pow(c,d,n)
print mingwenint
3.Marvin is plain Jane
根据题目提示这是Menezes-Vanstone加密(题中提到他的朋友叫menezes或van-stone),这里简单介绍一下Menezes-Vanstone加密,有利于理解下面的内容,Menezes-Vanstone加密是基于椭圆曲线的加密方案,在椭圆曲线上去一个基点G(x,y),A,B选择随机数da,db作为密钥,然后就可以得到公钥DA=da*G,DB=db*G。A将明文M转化为二元组m(m1,m2),然后计算(x1,y1)=da*Db,最后计算x2=(m1*x1)modp,y2=(m2*y1)modp组成二元组(x2,y2)即为密文,而B拿到密文后计算(x1,y1)=db*Da,则可以得到m1=(x2*x1^(-1))modp,m2=(y2*y1^(-1))modp,将m1和m2组合即可。在这道题中提到的brainpool p256r1经查询是椭圆曲线中的一个标准(在rfc5639中),可查到该椭圆曲线的一些标准,而在这里我们已知了二元组m中m1(文中反复提到的"Marvin is"),以及m加密后的(x2,y2),而(x1,y1)所在的椭圆曲线已知(brainpool p256r1),那么首先计算x1=x2*m1^(-1),根据椭圆曲线得到x1对应点y1,在计算m2=y2*y1^(-1)即可得到答案。
def txt(istr):
return int(istr.encode("hex"),16)
x1 = txt("Marvin is")
y1 = 71164450240897430648972143714791734771985061339722673162401654668605658194656
y2 = 12951693517100633909800921421096074083332346613461419370069191654560064909824
p = 0xA9FB57DBA1EEA9BC3E660A909D838D726E3BF623D52620282013481D1F6E5377
A = 0x7D5A0975FC2C3057EEF67530417AFFE7FB8055C126DC5C6CE94A4B44F330B5D9
B = 0x26DC5C6CE94A4B44F330B5D9BBD77CBF958416295CF7E1CE6BCCDC18FF8C07B6
#这里使用Tonelli-shanks算法寻找整数x使得a=(x^2)modp成立
def modular_sqrt(a, p):
if legendre_symbol(a, p) != 1:
return 0
elif a == 0:
return 0
elif p == 2:
return p
elif p % 4 == 3:
return pow(a, (p + 1) / 4, p)
s = p - 1
e = 0
while s % 2 == 0:
s /= 2
e += 1
n = 2
while legendre_symbol(n, p) != -1:
n += 1
x = pow(a, (s + 1) / 2, p)
b = pow(a, s, p)
g = pow(n, s, p)
r = e
while True:
t = b
m = 0
for m in xrange(r):
if t == 1:
break
t = pow(t, 2, p)
if m == 0:
return x
gs = pow(g, 2 ** (r - m - 1), p)
g = (gs * gs) % p
x = (x * gs) % p
b = (b * g) % p
r = m
#这里使用Euler's criterion判别是否存在整数x使得a=(x^2)modp成立
def legendre_symbol(a, p):
ls = pow(a, (p - 1) / 2, p)
return -1 if ls == p - 1 else ls
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('modular inverse does not exist')
else:
return x % m
def gety(x):
y = modular_sqrt(x**3 + A * x + B, p) % p
y2 = -y % p
return y,y2
def hextotext(nbr):
s = hex(nbr)[2:-1]
if len(s) % 2 ==1:
s = "0"+s
return s.decode("hex")
x1_inv = modinv(x1, p)
c1 = (y1 * x1_inv) % p
c2_1, c2_2 = gety(c1)
print repr(hextotext(y2*modinv(c2_1, p) % p))
print repr(hextotext(y2*modinv(c2_2, p) % p))
5.RSAROLL
根据题意可知该题是使用了RSA加密,而在文件中给出了n,e和一些c,这里n比较小,很容易就可以分解成p,q,然后即可解出d,再对c解密发现他们都在128以内,使用ascii表转化组合即可得到答案
import gmpy2
n=920139713
p=18443
q=49891
e=19
d=int(gmpy2.invert(e,(p-1)*(q-1)))
c=[704796792,752211152,274704164,18414022,368270835,483295235,263072905,459788476,483295235,459788476,663551792,475206804,459788476,428313374,475206804,459788476,425392137,704796792,458265677,341524652,483295235,534149509,425392137,428313374,425392137,341524652,458265677,263072905,483295235,828509797,341524652,425392137,475206804,428313374,483295235,475206804,459788476,306220148]
ch=""
for i in c:
m=pow(i,d,n)
ch+=chr(m)
print ch6.神秘字母
阅读链接中的文字可知该加密是hill加密,对密文进行hill解密即可
from numpy import *
a=mat([[1,2],[0,1]])
a=a.I
mistr="dloguszijluswogany"
i=0
mingstr=""
while i0 and ch<=26:
mingstr+=chr(int(ch)+ord('a')-1)
for j in xrange(-2,2):
ch=26*j+c[1][0]
if ch>=0 and ch<26:
mingstr+=chr(int(ch)+ord('a')-1)
print mingstr 7.我喜欢培根
打开文件发现是摩斯电码,解密,发现结尾可能是培根解密,而根据题目提示可以确定,求解。
#encode=utf-8
s='-- --- .-. ... . ..--.- .. ... ..--.- -.-. --- --- .-.. ..--.- -... ..- - ..--.- -... .- -.-. --- -. ..--.- .. ... ..--.- -.-. --- --- .-.. . .-. ..--.- -.. -.-. -.-. -.. -.-. -.-. -.-. -.. -.. -.. -.-. -.. -.-. -.-. -.-. -.. -.. -.-. -.-. -.-. -.-. -.-. -.-. -.-. -.-. -.-. -.. -.. -.-. -.. -.-. -.-. -.-. -.-. -.. -.-. -.-. -.-. -.-. -.-. / -.-. -.. -.-. -.-. -.-. -.. -.-. -.-. -.. -.-. / -.-. -.-. -.-. -.. -.-. -.-. -.. -.. -.. -.-. -.-. -.. -.. -.. -.-. -.-. -.. -.-. -.. -..'
codebook = {
'A':".-",'B':"-...",'C':"-.-.",'D':"-..",'E':".",'F':"..-.",'G':"--.",'H':"....",'I':"..",'J':".---",'K':"-.-",'L':".-..",'M':"--",'N':"-.",'O':"---",'P':".--.",'Q':"--.-",'R':".-.",'S':"...",'T':"-",'U':"..-",'V':".--",'W':".--",'X':"-..-",'Y':"-.--",'Z':"--..",'1':".----",'2':"..---",'3':"...--",'4':"....-",'5':".....",'6':"-....",'7':"--...",'8':"---..",'9':"----.",'0':"-----",'.':".━.━.━",'?':"..--..",'!':"-.-.--",'(':"-.--.",'@':".--.-.",':':"---...",'=':"-...-",'-':"-....-",')':"-.--.-",'+':".-.-.",',':"--..--",'\'':".----.",'_':"..--.-",'$':"...-..-",';':"-.-.-.",'/':"-..-.",'\"':".-..-.",'&':"...."
}
codebook3 = {
'A':"CCCCC",
'B':"CCCCD",
'C':"CCCDC",
'D':"CCCDD",
'E':"CCDCC",
'F':"CCDCD",
'G':"CCDDC",
'H':"CCDDD",
'I':"CDCCC",
'J':"CDCCD",
'K':"CDCDC",
'L':"CDCDD",
'M':"CDDCC",
'N':"CDDCD",
'O':"CDDDC",
'P':"CDDDD",
'Q':"DCCCC",
'R':"DCCCD",
'S':"DCCDC",
'T':"DCCDD",
'U':"DCDCC",
'V':"DCDCD",
'W':"DCDDC",
'X':"DCDDD",
'Y':"DDCCC",
'Z':"DDCCD",
}
def decode(s):
cipher=""
i=0
while i8.Strength
打开文件发现顶部写着n,e,c,说明这是rsa加密,而再仔细看这里的所有n相同,猜测这里是相同明文在不同公钥加密而来的结果,而n有相同,所以这里可以使用rsa共模攻击,只需找到两个互质的e即可
import gmpy2
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def shuchu(mingwenstr):
if mingwenstr[len(mingwenstr)-1]=='L':
mingwenstr=mingwenstr[2:len(mingwenstr)-1]
else:
mingwenstr=mingwenstr[2:len(mingwenstr)]
if not len(mingwenstr)%2==0:
mingwenstr='0'+mingwenstr
i=len(mingwenstr)
mingwen=""
while i>=1:
str1=mingwenstr[i-2:i]
if int(str1,16)>33 and int(str1,16)<126:
mingwen=chr(int(str1,16))+mingwen
else :
mingwen=" "+mingwen
i=i-2
print mingwen
list1=[{'e':0x1614984a0df,'c':0x7ded5789929000e4d7799f910fdbe615824d04b055336de784e88ba2d119f0c708c3b21e9d551c15967eb00074b7f788d3068702b2209e4a3417c0ca09a0a2da4378aa0b16d20f2611c4658e090e7080c67dda287e7a91d8986f4f352625dceb135a84a4a7554e6b5bd95050876e0dca96dc21860df84e53962d7068cebd248dL},
{'e':0x15ef25e10f54a3,'c':0x7c5b756b500801e3ad68bd4f2d4e1a3ff94d049774bc9c37a05d4c18d212c5b223545444e7015a7600ecff9a75488ed7e609c3e931d4b2683b5954a5dc3fc2de9ae3392de4d86d77ee4920fffb13ad59a1e08fd25262a700eb26b3f930cbdc80513df3b7af62ce22ab41d2546b3ac82e7344fedf8a25abfb2cbc717bea46c47eL},
{'e':0x1da0ca25f5a8d,'c':0x65af8559c93c05efecb6a3029dce7e831787878d5539f7b20fc7645ef4892cee23f53384377180a8789e2b2697b7f07fe1e02f3c6b4bb583a072cf27867f558bd51bdc4880b522e2e81c6572b5629241a601acda31356a4fc7767f6a54163f6d16a0bfb6f577c6662e6e1dee78dc6dc51b4d719a1de3d9c2cb5c41a6987cf2b2L},
{'e':0xc2eac4c2b,'c':0x711892a29a738e3ac3b996427e4188f23d1c63d9d9c962bfd65b675698e432f27f0ce4e42101576dacaf7b8c78851d406a2695142103d39fbbdd0c111a8587af65834546a5efa8ab6d622a7408d485fe910aaa3ce44168508ab03ad69b15855913c31406be650a492aad1ddde05ac6e655fd842be659ceed886ec6cae8476f1dL},
{'e':0x1a6c23,'c':0x57ab8d4c79a58718c0db0dd62a8ba97883e03cd7d14cc3366108a37e8998fc55abd555ca54f81fc975c64e1374d253d95cd957bbb26780e09ca411e8c29742de3414e7cf3f572aea0c35c99b733533e3d39efd5c6c2ce28e67831fb7ecb59186ee791670ffaa08eb6f44614553ec89f7cd5fded09c7c14603e5234f63deb3cf9L},
{'e':0x2beccafd,'c':0x6630d2faf104547351da66f760fde920203a041b82f07c0db9034148f9dd17c1f14c2c8ec95ae64e8d0b546f58b998c0412046d48d6057758df3ca300d75106d1ad3210bfce28cd17eebb0fe453d954809aff7ff0fa3044adc6162cfd295cc1d28789e718489c70658758818e5150c09c8fd242d8d5b3699970b042e773b6f7aL},
{'e':0x280554063943,'c':0x5bcc5f5435fd087c9615bf04864a82a8fed19576fd311cfde565ca340303cd72d3842ad7a8de9c7123cacbcb9b8be1af01590ef19ff0ebf71e5fec2314639c0d5626cd9ee74fbc8a21325778ba3ef3e1ea310e51b029b5ff9b162b881a240ef4f285dc3a40f62e8a1267e9d6fb3d425509dedefc05ab38f4db5b3f47ddc7619bL},
{'e':0x23b0d,'c':0x48bd06fba0691da8883286c21cd49e02eb65d0e3b6ee12b2113940cc64d9f6b921fcb6a8aa82aac592e6a9552d9e27d80e5061501892ec1227ab24dca4236474502156dce8f852eebcbe515c79d998037f55b00858bd16c4ea6fb7b4bea193f6893be766f234b1aa0a38eebaefc2a11264493ea11fb2c103a7552968d8f808bcL},
{'e':0x6b8a5ae7,'c':0x6fdcbfb5cd2cacd032ef7200fd49b9f304a6dbd8399f4a91a72d1d9150f97b3b513f44dfc56f6f7c8ec41a8ef9b93a80230a1e65e29d2ef519bb83931d4b0c7a589059cfdf2d571660ab790a9c7e085e3018bf19748abd6d521952b68bc9594c1ad34726658bd9bd445d3b6381ceee57328838e8a129867e505be0ca0d1a1da5L},
{'e':0x360f1c91fed,'c':0xa149bb3969479d5b9eff15099ce863d36899d1146c731a91db91ef15869358df4dbe82eaca128d5cd977eeafcb306f949603e5261e9262820f890f8b5dd145718d7af46590eb6474883fe38f399a724d027e04b015d76fd98376d1c5a6d2f63cbc95f15d523692180ca505b327255a67294e5eb69157b3c1230818ac116e48eeL},
{'e':0xefe30ec7dabb,'c':0x6fce7de911abe59864e01b9b306c167bdde17da28dfcfb7b3c768ec47d0ae4160cebedae9e482468c65c412eab54ed5d422c3b7b7f818fb6813412b0c1d710f02c763a3cbe4a24140f7a48f543190bfc61a838344ce13e093728a285ec9671c93230aa6abb5f52b83e3f065c9fef894c6c2cb17176e8c2c5cb09f03300de66abL},
{'e':0x753fdb5,'c':0xa2403b99c19c2a882bbca51ee414486e1d60db003d16fdf8f30290bae586aaa5500c74b6e8dfe7a3081092da567fd38c57fa04e8a49a94daf229ede6e27fe2571420025aafe123e95b3bcf00a7b64a5e5f48528c8788303c148a4558ab4104b58b2846fde31466f2540b9c5926ffeebfd540ab8da05f9a82db791d72806b74ffL},
{'e':0x12546aff963f4b6b35fL,'c':0x7293cec4d46c8073ce78b4ec8d97c086124376cf75fbcc4c0a57159b02e9c7a8545d4fa73f89b0f05d99371b56a565f3b08c8c9725f4f07a513e21c26c4e2a60984ace3f38dab7d84b1208a1a80147377f2552ab040fae4d151939f094543276a823674659dc8de329e47765a8ece154bc9a1aaacee2c7de58876b706690c0cfL},
{'e':0x11d2843e693,'c':0x9d96bc542c7afe105b6415d7f0f6d55114d81761f46bfaebbfbf36188f9fbc3759c4693645f4605d17611b9324386333ab0d44505737a8b9a9e73a71fb698f1d0a57fa1e99b18aae8f728a6cee9d774df4ebb5835c9b844ee77817ca04dab9f3cd0ff085c5001100d5e08df98bd1eb6597fb5c1ddf6afd787b2d5274fa03eb7fL},
{'e':0x9d540226f,'c':0x4c17528a0d1e36030f882d9c1060ccf974e48178cb7c4c8630968846ca668773881e41a780ba686315ccc487bd12c4389271c51a2c63306b78a2b2f8d8d7736f3ac35d65c9702a5f45d064aa1c7b43cbf2a0723becd8694c325f75d3ef8bf8703690da625c2b139e816bc070f9126067912317d0a3c59e24b87ed611e285e5deL},
{'e':0xee4c39df4ed4c0f,'c':0x9fdf693d41e020a9eff786f87f12dc2e2b518ecaa178c8991d06a3ef2e8e136aba94441bc8dbd5be69b05621b635f244afc0f8f5114b7e4c9ace80bb53163acf67bfd4af4ffc5b5bb727c3a0abf794a6494a425ff0e4c08d967dd3ab0e58f4b573d539c5a55a2cecd3d043f23faf2554b6c11c8e25f90084ac0474ee70b70c3bL},
{'e':0x213901ef4052b8b251c3L,'c':0xefa14d35d75b629673e8d983f1253134e4584ef16fd13618b23ea4e281f775942d370b384cf2888fb92b3e2f83d1a21448d16676efc9b824afb8992c6fa98530ba28d01fb81fe060ee67f065018562ea513f4da00e00e8a5b3efa966825577960318790f1f76f97f6fd72dde80d0a649687e3237efda595c50da1cf105c1138L},
{'e':0xe93f,'c':0x2e1622191a5d6092ef23dabb82bdbf0f5f9eb018f27184c05512679a38be06fc23ca57c1bd4129720e5d562ffebdb30034c655aaea0b78fb996a7264b665488c8c703f1f0169a37688497ab715a4c6bbc5db5839e6800d5f79129c3f2155ad6a07edbaf8f2dfe524c68a41cf7456bf87e2367ded2a8387a6fdc812589375f25cL},
{'e':0x4042c3955,'c':0x8caeaa7d272f9606fee9222efd1d922143db738b95bd64746b27bc4c0fd979a2c57b4735131a4391a81bf5f0c0c8eea41d4f91bed4d17784b1956fd89882b97c98009051ac3a03964499c864524d3ddc10299c0290e91707b62ce89b118afe558151be39d61de0483def52c6cb546132ecab85143715bc593a2892b1e41b37b9L},
{'e':0x61553816b407935,'c':0x9eade5cb88d453b00c0558f76ab78dc76537588ed1212ffdfdc4ecff98c55457a4b581d157901131c32936d09b6a18238ab243bc40c90af4c73741cd2fc122b8803680b2609eba6af1215a94017ad6d2840203532e3268b7b7dc50c541c281069f1c4b243bff83520481adb5e2b3386bd14c91df1a4b70d2a6b2c725e3e880f2L}]
n=0xa5f7f8aaa82921f70aad9ece4eb77b62112f51ac2be75910b3137a28d22d7ef3be3d734dabb9d853221f1a17b1afb956a50236a7e858569cdfec3edf350e1f88ad13c1efdd1e98b151ce2a207e5d8b6ab31c2b66e6114b1d5384c5fa0aad92cc079965d4127339847477877d0a057335e2a761562d2d56f1bebb21374b729743L
gcdlist=[]
for i in xrange(0,len(list1)):
j=i+1
while j9.唯密文攻击
根据后面作者提示可知,在200个密文中有一个明文与n有公因子,找到这个明文,求出其与n的公因子,即可找到n的素因子中最小的那个,求其md5值按要求填入答案即可
import hashlib
def gcd(a,b):
if b>a:
temp=a
a=b
b=temp
c=1
while not c==0:
c=a%b
a=b
b=c
return a
list1=[]
file = open("ciphertext.txt")
line = file.readline()
n=file.readline()
n=int(n)
while 1:
line = file.readline()
if not line:
break
elif line[0]>='0' and line[0]<='9':
list1.append(line)
file.close()
for i in list1:
b=int(i)
if not gcd(n,b)==1:
g=gcd(n,b)
break
ga=n/g
if ga>g:
print (hashlib.md5(str(g)).hexdigest()).upper()[:6]
else:
print (hashlib.md5(str(ga)).hexdigest()).upper()[:6]
10.RSA
下载文件打开,发现开头有“pk”,猜测只是zip压缩文件(可用binwalk检测),添加后缀后解压,发现enc文件和pem文件,pem文件打开时openssl的公钥文件,而enc不是数据包文件,所以enc文件应该时公钥文件加密后的密文文件,使用openssl得到RSA的n,e,用yafu对n分解获得p,q,从而得到d,用密钥(n,d)对密文解密即可
import sys
import os
import gmpy2
def shuchu(mingwenstr):
if mingwenstr[len(mingwenstr)-1]=='L':
mingwenstr=mingwenstr[2:len(mingwenstr)-1]
else:
mingwenstr=mingwenstr[2:len(mingwenstr)]
if not len(mingwenstr)%2==0:
mingwenstr='0'+mingwenstr
i=len(mingwenstr)
mingwen=""
while i>=1:
str1=mingwenstr[i-2:i]
if int(str1,16)>33 and int(str1,16)<126:
mingwen=chr(int(str1,16))+mingwen
else :
mingwen=" "+mingwen
i=i-2
print mingwen
p=258631601377848992211685134376492365269
q=286924040788547268861394901519826758027
e=65537
n=p*q
d=int(gmpy2.invert(e,(p-1)*(q-1)))
with open("flag.enc" , "rb") as f:
s=f.read()
miwen=long(s.encode('hex'),16)
mingwenint=pow(miwen,d,n)
mingwenstr=hex(mingwenint)
shuchu(mingwenstr)
11.NSCTF crypto200
这个题准确的说应该是一道隐写题,下载得到一张图片,放入stegsolve中,发现在blue plane 0时这是个二维码,对其反色扫描即可得到答案
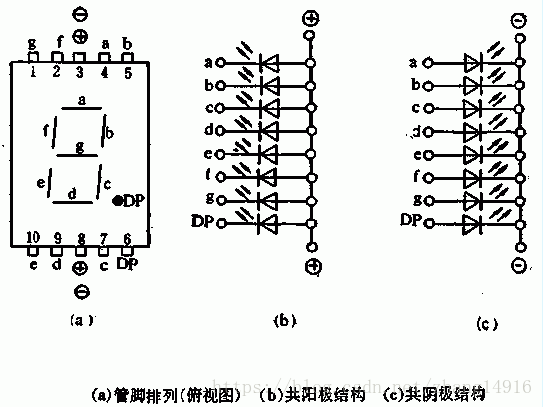
12.数码管
打开文件发现一张数码管的图片,查询有关数码管的资料,得知一个数码管需要8个电位(即0,1)控制,而且有共阴显示和共阳显示两种(即发光对应高电位还是低电位),这里的8个电位可组成一个ascii值,而颜色的不同是表示是其是否发光所对电位不同,尝试求解即可(从dp到a为从二进制高位到低位的方向)
13.压缩的问题
打开链接,发现一串16进制字符串,看开头就知道这大概是rar文件,用winhex将16进制写入文件,生成rar文件,解压,发现需要密码,根据题目提示取出65h-71h字符输入,解压成功,获得txt文件,计算文件sha1值输入即可(可直接使用linux下命令)
from hashlib import sha1
sha1Obj = sha1()
with open("秒破测试By天易love.txt", 'rb') as f:
sha1Obj.update(f.read())
print sha1Obj.hexdigest()[:8]