算法:动态规划经典题目
做一个简单整理与汇总。详情见给出的链接。
算法之美:动态规划
1. 最大子数组和问题——O(N)
关键思路:考虑数组的第一个元素,以及最大的一段数组(A[i], ..., A[j]),和A[0]的关系,有一下几种情况:
(1)当0 = i = j 时,元素A[0]本身构成和最大的一段;
(2)当0 = i < j 时,和最大的一段以A[0]开始;
(3)当0 < i 时, 元素A[0]和最大的一段没有关系。
Start = max( A[i], A[i] + Start);
All = max(Start, All);
核心代码:单层for循环
int MaxSubString(int* A, int n)
{
int Start = A[n - 1];
int All = A[n - 1];
for(int i = n - 2; i >= 0; i--) //从后向前遍历,反之亦可。
{
Start = max( A[i], A[i] + Start);
All = max(Start, All);
}
return All[0]; //All[0] 中存放结果
}2. 基础背包问题——O(N*V)
简单描述:有N件物品和一个容量为V的背包。第i件物品的体积是c[i],价值是v[i]。求解将哪些物品装入背包可使价值总和最大。特点是:每种物品仅有一件,可以选择放或不放。
关键思路:
如果一个问题的最优解包含了物品n,即Xn = 1,那么其余X1, X2, .....,Xn-1 一定构成子问题1,2,.....,n-1在容量C - cn时的最优解。
如果这个最优解不包含物品n,即Xn = 0; 那么其余 X1, X2.....Xn-1一定构成了子问题 1,2,....n-1在容量C时的最优解。
f[i][v] = max{ f[i-1][v] , f[i-1][v - c[i]] + w[i]}
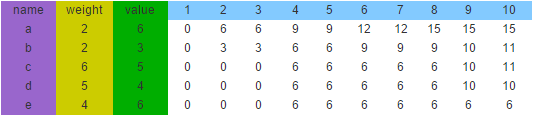
见下图,顺序为左下到右上。(仅供理解,代码与图不匹配)
核心代码:双层for循环:物品i、体积j
#include
#define max(a,b) ((a) > (b) ? a : b)
int c[5] = {3,5,2,7,4};
int v[5] = {2,4,1,6,5};
int f[6][10] = {0};
//f[i][v] = max{ f[i-1][v] , f[i-1][v - c[i]] + w[i]}
int main()
{
for(int i = 1; i < 6; i++)
for(int j = 1; j < 10 ;j++)
{
if(c[i] > j)//如果背包的容量,放不下c[i],则不选c[i]
f[i][j] = f[i-1][j];
else
{
f[i][j] = max(f[i-1][j], f[i-1][j - c[i]] + v[i]);//转移方程式
}
}
std::cout< 3. 矩阵联乘问题——O(N^3)
简单描述:给定n个矩阵{A1,A2,...,An},矩阵A1的维数为p(i-1)×p(i), i = 1,2, ..., n,设p数组为[30,35,15,5,10,20,25].
如何给矩阵连乘A1*A2*....*An完全加上括号使用矩阵乘法中计算次数最少。
关键思路:假定问题Ai*Ai+1*...Aj被完全加括号的最优方式是在Ak与Ak+1之间被分裂,设m[i,j]表示计算Ai...j所需的最小计算次数。
m[i,j] = min{m[i,k]+m[k+1,j]+p(i-1)*p(k)*p(j) }
见下表输出:
数组m如下,m[1,6]是需要的解。
[[0, 0, 0, 0, 0, 0, 0],
[0, 0, 15750, 7875, 9375, 11875, 15125],
[0, 0, 0, 2625, 4375, 7125, 10500],
[0, 0, 0, 0, 750, 2500, 5375],
[0, 0, 0, 0, 0, 1000, 3500],
[0, 0, 0, 0, 0, 0, 5000],
[0, 0, 0, 0, 0, 0, 0]]数组middle如下:[[0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 3, 3, 3],
[0, 0, 0, 2, 3, 3, 3],
[0, 0, 0, 0, 3, 3, 3],
[0, 0, 0, 0, 0, 4, 5],
[0, 0, 0, 0, 0, 0, 5],
[0, 0, 0, 0, 0, 0, 0]]核心代码:三层for循环——增量、起点、划分点
void main()
{
int n=7,min;
int m[n][n],middle[n][n];
int r[n] = {30,35,15,5,10,20,25}; /* 矩阵维数 */
/* 初始化 */
memset(m,0,sizeof(m));
for (int a = 1; a < n-1; a++) // 确定增量,最大为n-1
{
for (int i = 1; i <= (n-1) - a; i++) // 确定差值为a的两个数i与j
{
j = i + a;
min = m[i][i] + m[i+1][j] + r[i-1] * r[i] * r[j]; // 初始化最小值,即k=i时候
middle[i][j] = i;
for (int k = i + 1; k < j; k++) //遍历不同k分点,并记录最小值及最小值得划分点
{
if (min > m[i][k] + m[k+1][j] + r[i-1] * r[k] * r[j])
{
min = m[i][k] + m[k+1][j] + r[i-1] *r[k]* r[j];
middle[i][j] = k;
}
}
m[i][j] = min;
}
}
std::cout<
4. 完美平方数
简单描述:给定一个数,求其最少能表示成几个完全平方数的和表示。
关键思路:核心代码:
# coding:utf-8
import math
class Solution(object):
def numSquares(self,n):
def isSquare(m):
b=int(math.sqrt(m))
return b*b == m
a=[float("inf") for i in range(n)]
if (n==0 or n==1 or isSquare(n)):
print "1"
return 1
for i in range(1,n+1): # 依次计算每个数的最小平方次数,从1到n
if isSquare(i):
a[i-1]=1;
else:
for j in range(1,i): # 动态规划
a[i-1] = min(a[j-1] + a[i-j-1],a[i-1])
print a[n-1]
# print a
return 1
def __init__(self,n):
self.numSquares(n)
S=Solution(20)