置信区间
作者:chen_h
微信号 & QQ:862251340
微信公众号:coderpai
介绍
在统计中,置信区间用于表示可能存在正确答案的范围。他们是量化不确定性的优雅方式,在统计测试的许多部分中它是无处不在的。
样本均值和总体均值
样本均值和总体均值是不同的,通常,我们想要了解总体均值,但我们只能计算样本均值。然后,我们希望使用样本均值来估计总体均值。我们使用置信区间来尝试确定我们的样本均值估计总体均值的准确程度。
置信区间
如果我要求你估计美国女生的平均身高,你可以通过测量 10 名女生的身高,然后估计该样本的平均值来计算总体均值。接下来让我们来试试吧:
import numpy as np
import seaborn as sns
from scipy import stats
import matplotlib.pyplot as plt
# We'll set a seed here so our runs are consistent
np.random.seed(10)
# Let's define some 'true' population parameters, we'll pretend we don't know these.
POPULATION_MU = 64
POPULATION_SIGMA = 5
# Generate our sample by drawing from the population distribution
sample_size = 10
heights = np.random.normal(POPULATION_MU, POPULATION_SIGMA, sample_size)
print(heights)
mean_height = np.mean(heights)
print('sample mean: ', mean_height)
[70.65793252 67.57639487 56.27299854 63.95808075 67.10667987 60.3995722
65.32755793 64.54274263 64.02145715 63.12699895]
sample mean: 64.29904154070394
不幸的是,简单的计算样本均值对我们没有太大作用,因为我们不知道它与总体均值的关系。为了了解它的相关性,我们可以查看样本中存在多少差异,方差越大表明不稳定和不确定性越大。
print('sample standard deviation: ', np.std(heights))
sample standard deviation: 3.759878018454642
这对我们来说仍然不够,真正了解我们的样本均值和总体的关系意味着我们需要计算标准误差。标准误差是样本均值方差的度量。
重要的事!!!
计算标准误差设计假设你采样的方式,并且数据是正常且独立的。如果违反这些条件,你的标准误差将是误差的。标准误差的公式是:
S E = σ n SE = \frac{\sigma}{\sqrt{n}} SE=nσ
其中, σ \sigma σ 是标准偏差, n n n 是样本数。
SE = np.std(heights) / np.sqrt(sample_size)
print('standard error: ', SE)
standard error: 1.1889778262717268
Scipy 的统计库中有一个函数用于计算标准误差。请注意,默认情况下,此功能包含通常不需要的自由度矫正(对于足够大的样本,它实际上是无关紧要的)。你可以通过将参数 ddof 设置为 0 来省略校正。
stats.sem(heights, ddof=0)
1.1889778262717268
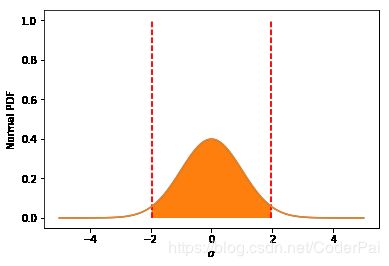
假设我们的数据是正太分布的,我们可以使用标准误差来计算置信区间。为此,我们首先设置所需的执行水平,比如 95%,然后我们确定有多少标准偏差包含 95% 的质量。事实证明,在标准正太分布上,95% 的系数是位于 -1.96 和 1.96 之间的。当样本足够大时(通常 > 30 作为阈值),中心极限定理适用,并且可以安全的假设正态性。如果样本量较小,则更安全的方法是使用具有适当指定自由度的分布。计算值的实际方法是使用累积分布函数(CDF)。如果你不熟悉(CDF),反向CDF及其伴随PDF,你可以阅读这几个链接,1,2,3。
注意:在应用中心极限定理时要小心,因为金融中的许多数据集基本上是非正太的,并且随意应用定理或不注意微妙性是非常不安全的。
我们可以在这里可视化 95% 置信区间:
# Set up the x axis
x = np.linspace(-5,5,100)
# Here's the normal distribution
y = stats.norm.pdf(x,0,1)
plt.plot(x,y)
# Plot our bounds
plt.vlines(-1.96, 0, 1, colors='r', linestyles='dashed')
plt.vlines(1.96, 0, 1, colors='r', linestyles='dashed')
# Shade the area
fill_x = np.linspace(-1.96, 1.96, 500)
fill_y = stats.norm.pdf(fill_x, 0, 1)
plt.fill_between(fill_x, fill_y)
plt.xlabel('$\sigma$')
plt.ylabel('Normal PDF');
plt.show()
一些诀窍
现在,我们可以计算一个区间,而不是报告我们的样本均值没有任何正确的概率,我们可以计算一个区间,并且更有信心总体均值位于该区间内。为此,我们采用样本均值和区间: ( μ − 1.96 S E , μ + 1.96 S E ) (\mu - 1.96SE, \mu + 1.96SE) (μ−1.96SE,μ+1.96SE) 。
这是有效的,因为我们假设正太分布 。
细微之处
在任何给定的情况下,估计的真实值和置信区间的界限是固定的。说“全国平均女性身高在 63 到 65 英寸之间,概率为 95%” 是不正确的,但不幸的是,这是一个非常常见的误解。相反,95% 指的是这样一个事实:在 95% 置信区间的许多计算中,真实值将在 95% 的情况下在区间内。但事实上,对于单个样本和从中计算的单个置信区间,我们无法评估区间包含总体均值的概率。下面的可视化演示了这一点。
在下面的代码块中,有两点需要注意。首先,虽然样本来那个足够大到保持正太,但我们使用分布只是为了演示我们是如何使用它的。其次,所需的值(类似于上面的使用)是根据反向累积密度函数计算的,即 scipy.stats 中的 ppf 。
np.random.seed(8309)
n = 100 # number of samples to take
samples = [np.random.normal(loc=0, scale=1, size=100) for _ in range(n)]
fig, ax = plt.subplots(figsize=(10, 7))
for i in np.arange(1, n, 1):
sample_mean = np.mean(samples[i]) # calculate sample mean
se = stats.sem(samples[i]) # calculate sample standard error
h = se*stats.t.ppf((1+0.95)/2, len(samples[i])-1) # calculate t; 2nd param is d.o.f.
sample_ci = [sample_mean - h, sample_mean + h]
if ((sample_ci[0] <= 0) and (0 <= sample_ci[1])):
plt.plot((sample_ci[0], sample_ci[1]), (i, i), color='blue', linewidth=1);
plt.plot(np.mean(samples[i]), i, 'bo');
else:
plt.plot((sample_ci[0], sample_ci[1]), (i, i), color='red', linewidth=1);
plt.plot(np.mean(samples[i]), i, 'ro');
plt.axvline(x=0, ymin=0, ymax=1, linestyle='--', label = 'Population Mean');
plt.legend(loc='best');
plt.title('100 95% Confidence Intervals for mean of 0');
plt.show()