八大排序算法、稳定性及时间复杂度

①、什么是稳定性？

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

②、什么是时间复杂度？

计算机科学中，算法的时间复杂度是一个函数，它定性描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。

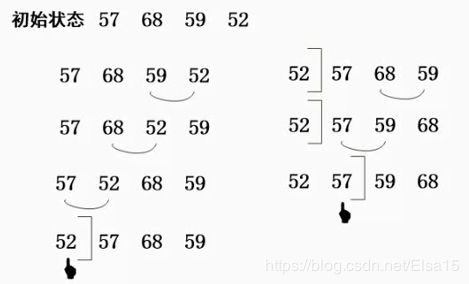
1、直接插入排序

在插入第i个记录时，R1,R2,R3...Rn已经排好序，这时将Ri的关键字ki依次与关键字ki-1,ki-2进行比较，从而找到插入的位置。

从图可以看出，插入排序是从第一个元素开始，进行两两比较，把小的放到前面。

如果碰到一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序并没有发生变化，所以插入排序是稳定的。

时间复杂度：O(n²）

2、冒泡排序

从序列的最后一位开始，两两比较，每当两相邻的数比较后，发现它们的排序与要求的排序相反时，就将他们互换。

从图可以看出， 冒泡排序是从最后一个元素开始的，进行两两比较。遇到相同的元素时，便放到相同元素的后面，所以此排序也是稳定的。

时间复杂度与插入排序一样O(n²）

3、简单选择排序

在要排序的一组数中，选出最小（或者最大）的一个数与第1个位置的数交换，然后在剩下的数当中再找最小（或者最大）的与第2个位置的数交换，以此类推，直到倒数第二个与倒数第一个比较为止。

在此排序方法中，相同的两个数顺序可能会被调换，所以此排序不稳定。

时间复杂度： O(n²）

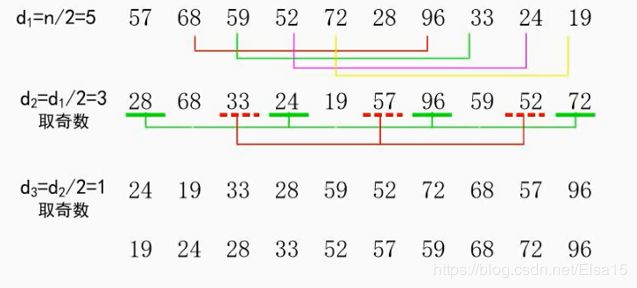
4、希尔排序（缩小增量排序）

先将整个待排序的记录序列分割成若干个子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，在对全体记录进行依次直接插入排序。

由图可以看出，重复的数据49前后顺序转换，所以该排序是不稳定的。

时间复杂度为：O(n的1.3次方)

5、快速排序

第一步：在待排序的n个记录中任取一个记录，以该记录的排序码为准，将所有记录都分成两组，第一组都小于该数，第2组都大于该数，如图所示。

第二步：采用相同的方法对左右两组分别进行排序，知道所有记录都排到相对应的位置为止。

该算法的排序过程是二叉树过程，所以时间复杂度为O(nlogn)

因为是前后快速排序，所以不稳定。

6、堆排序

堆的定义如下：具有n个元素的序列（k1,k2,...,kn),当且仅当满足

时称之为堆。由堆的定义可以看出，堆顶元素（即第一个元素）必为最小项（小顶堆）。
若以一维数组存储一个堆，则堆对应一棵完全二叉树，且所有非叶结点的值均不大于(或不小于)其子女的值，根结点（堆顶元素）的值是最小(或最大)的。如：
(a) 大顶堆序列：(96, 83,27,38,11,09)
(b) 小顶堆序列：(12，36，24，85，47，30，53，91)

 该排序的时间复杂度O(nlogn)，不稳定。

7、归并排序

所谓“归并”是将两个或两个以上的有序文件合并成为一个新的有序文件。

归并排序时间复杂度为O(nlogn)，不稳定。

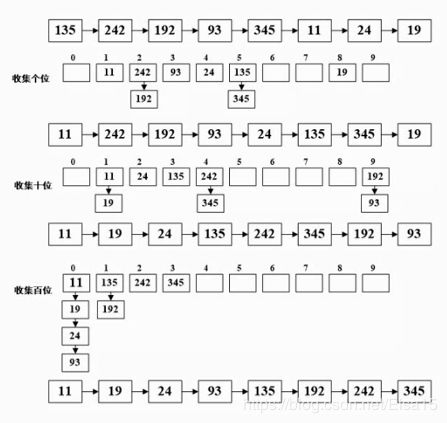
8、基数排序

 借助多关键字排序思想对单逻辑关键字进行排序的方法。基础排序不是基于关键字比较的排序方法，它适合于元素很多而关键字较少的排序。基数的选择和关键字的分解是根据关键字的类型来决定的。例如关键字是十进制数，则按个位、十位来分解。

概述：

①、稳定性判断：

从前往后或者从后往前，逐一（两两）进行比较的排序算法都具有稳定性的特征，如：冒泡排序，插入排序，基数排序，归并排序。

而较快比较出来的算法往往是不稳定的，如：快速排序，简单选择排序，堆排序，希尔排序。

②、时间复杂度判断：

涉及到两两递归或二叉树的排序时间复杂度为O(nlogn)，如堆排序，归并排序，快速排序