扩展卡尔曼滤波建模及应用
一、公式
1、卡尔曼滤波
![]()
![]()
![]()
![]()
![]()
A:状态向量 F:状态转移矩阵 P:状态协方差矩阵 Q:过程噪声矩阵 Z:测量向量 H:测量矩阵 R:测量噪声矩阵
本质上讲,建立卡尔曼滤波数学模型的过程就是建立以上矩阵的过程。
Kalman滤波基本的模型假设包括:
(1)系统的状态方程是线性的;
(2)观测方程是线性的;
(3)过程噪声符合零均值高斯分布;
(4)观测噪声符合零均值高斯分布;从而,一直在线性变化的空间中操作高斯分布,状态的概率密度符合高斯分布
使用卡尔曼滤波特别需要明确下面几点:
(1) 状态变量是什么?
(2) 状态方程是什么?
(3) 观测方程是什么?
2、扩展卡尔曼滤波
![]()
![]()
![]()
![]()
![]()
推导:卡尔曼滤波(Kalman Filter)原理与公式推导
二、应用
1、毫米波雷达跟踪目标建模过程
毫米波雷达观察世界的方式与激光雷达有所不同。激光雷达测量的原理是光的直线传播,因此在测量时能直接获得障碍物在笛卡尔坐标系下x方向、y方向和z方向上的距离;而毫米波雷达的原理是多普勒效应,它所测量的数据都是在极坐标系下的。
如下图所示,毫米波雷达能够测量障碍物在极坐标下离雷达的距离ρ、方向角ϕ以及距离的变化率(径向速度)ρ',如下图所示。
以2维的匀速运动为例,状态向量x为:
根据
F矩阵为
状态协方差矩阵P需要设定初值,在后续迭代过程会自动更新:
在扩展卡尔曼滤波过程中,Q和R矩阵的大小会影响卡尔曼增益K的大小,进而影响整个滤波器预测和观测的占比。
卡尔曼滤波的Q矩阵要比R矩阵更难准确获得,因此,先确定R矩阵,之后经验性地给定Q矩阵,观察滤波效果以决定对Q矩阵的调整。R矩阵一般可以根据传感器自身的属性给定。
扩展卡尔曼滤波中,由于系统是非线性的,H矩阵往往不能直接得到。
Z向量为:
![]() 为
为
毫米波雷达观测z是包含位置、角度和径向速度的3x1的列向量,状态向量x'是包含位置和速度信息的4x1的列向量,根据公式y=z-Hx'可知测量矩阵(Measurement Matrix)H的维度是3行4列。即:
从上面的公式很容易看出,等式两边的转化是非线性的,并不存在一个常数矩阵H,能够使得等式两边成立。
如果将高斯分布作为输入,输入到一个非线性函数中,得到的结果将不再符合高斯分布,也就将导致卡尔曼滤波器的公式不再适用。因此我们需要将上面的非线性函数转化为近似的线性函数求解。
非线性函数y=h(x)可通过泰勒公式在点(x0,y0)处展开为泰勒级数:
忽略二次以上的高阶项,即可得到近似的线性化方程,用以替代非线性函数h(x),即:
将非线性函数h(x)拓展到多维,即求各个变量的偏导数,即:
对x求偏导数所对应的这一项被称为雅可比(Jacobian)式。
我们将求偏导数的公式与我们的之前推导的公式对应起来看x的系数,会发现这里的测量矩阵H其实就是泰勒公式中的雅可比式。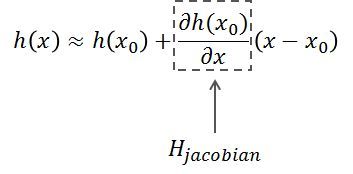
雅可比矩阵结果:
求得非线性函数h(x')对px,py,vx,vy的一阶偏导数,并排列成的矩阵,最终得到雅克比(Jacobian)矩阵H:
其中:
最终得到的雅克比矩阵H为:
根据以上公式可知,在每次预测障碍物的状态后,需要根据预测的位置和速度计算出对应的测量矩阵H,这个测量矩阵为非线性函数h(x')在x'所在位置进行求导的结果。
参考:https://zhuanlan.zhihu.com/p/63641680
卡尔曼滤波(kalman)相关理论以及与HMM、最小二乘法关系














