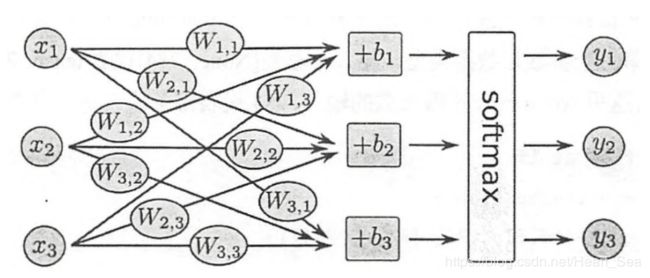
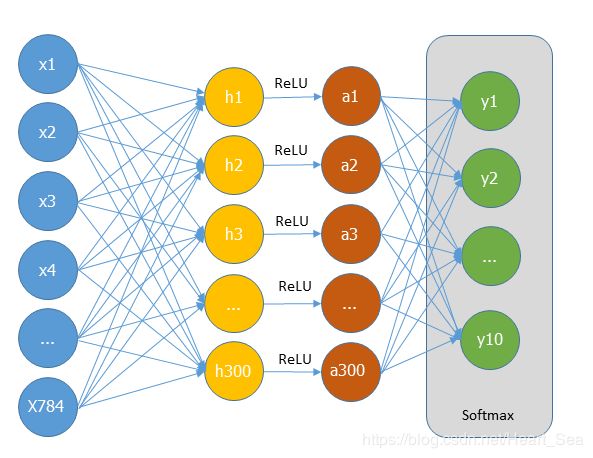
TensorFlow基于minist数据集实现手写字识别实战的三个模型
手写字识别
- model1:输入层→全连接→输出层softmax
- model2:输入层→全连接→隐含层→全连接→输出层softmax
- model3:输入层→卷积层1→卷积层2→全连接→dropout层→全连接→输出层softmax
model1:输入层→全连接→输出层softmax
"""
作者:Heart Sea
功能:实现softmax regression 识别手写数字
Model:
1个输入层
全连接
1个输出层 softmax,取概率值最大的那个
1.0:数据集位置与执行文件在同一个文件夹中
版本:1.0
日期:10/10/2019
"""
import tensorflow.examples.tutorials.mnist.input_data as input_data
mnist = input_data.read_data_sets("D:/software/pycharm/shizhan/softmax/MNIST_data/", one_hot=True)
print(mnist.train.images.shape, mnist.train.labels.shape) # 训练集
print(mnist.test.images.shape, mnist.test.labels.shape) # 测试集
print(mnist.validation.images.shape, mnist.validation.labels.shape) # 验证集
# (55000, 784) (55000, 10)
# (10000, 784) (10000, 10)
# (5000, 784) (5000, 10)
import tensorflow as tf
x = tf.placeholder(tf.float32, [None, 784]) # 创建输入数据的地方,数据类型float32,数据尺寸[None, 784]。None表示不限条数的输入,784是每条输入是一个784维的向量
W = tf.Variable(tf.zeros([784, 10])) # 创建权值参数矩阵,尺寸[784, 10]
b = tf.Variable(tf.zeros([10])) # 创建bias参数向量,尺寸[10],python执行结果是一行10列,matlab执行结果是10行10列
y = tf.nn.softmax(tf.matmul(x, W) + b) # 进行Softmax Regression算法,y是预测的概率分布,y的shape为(None, 10)
# softmax是tf.nn下面的一个函数,而tf.nn则包含了大量神经网络的组件。
# 训练模型
# 对多分类问题,经常使用交叉熵作为loss function
# softmax的交叉熵公式:对所有样本的交叉熵损失求和再平均,再负
# 计算交叉熵,判断模型对真实概率分布估计的准确程度
# y_ * tf.log(y)维度都是[None, 10],因此两者相乘(不是矩阵相乘),实质是对应行相乘
# 用 tf.reduce_sum 根据 reduction_indices=[1] 按照列,所有元素的总和(10个类别求和),
# tf.reduce_mean用来对每个batch数据求均值
y_ = tf.placeholder(tf.float32, [None, 10]) # 定义placeholder,y_是真实的概率分布
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))
# 选择随机梯度下降SGD以0.5的学习速率最小化交叉熵
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)
# 上面三行可改写为下面一行
# tf.global_variables_initiallizer().run()
for i in range(1000): # 模型循环训练1000次,从0开始,999结束
batch_xs, batch_ys = mnist.train.next_batch(100) # 随机抓取训练数据中的100个批处理数据点
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
# 完成模型训练
# 评估模型
# tf.argmax是从一个tensor中寻找最大值的序号,tf.argmax(y,1)求预测数字中概率最大的那一个,tf.argmax(y_,1)求样本的真实数字类别
# tf.equal 判断预测的数字类别是否就是正确的类别
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
# 用tf.cast将之前的correct_prediction输出的bool值转换为float32,再求平均值
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels})) #输入数据,计算准确率
# 0.9192
model2:输入层→全连接→隐含层→全连接→输出层softmax
"""
作者:Heart Sea
功能:tessorflow实现多层感知机/多层神经网络 Multi-Layer Perceptron, MLP
加入:减轻过拟合的Dropout, 自适应学习速率的Adagrad, 可解决梯度弥散的激活函数ReLU
Model:
1个输入层
全连接
1个隐含层, 激活ReLU, Dropout
全连接
1个输出层, softmax
版本:2.0
日期:10/10/2019
"""
# 载入tensorflow加载数据集mnist
from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
# 创建默认的InteractiveSession,后面各项操作无须指定session了
sess = tf.InteractiveSession()
in_units = 784 # 输入层节点数
h1_units = 300 # 隐含层节点数
# W1,b1为隐含层的权重和偏置
# W2,b2为输出层的权重和偏置,全部置为0,因为对于sigmoid,在0处最敏感,梯度最大
# 初始化参数W1为截断的正态分布,标准差为0.1
# 由于使用ReLU,需要使用正态分布给参数加噪声,来打破完全对称并且避免0梯度
# 在其他的一些模型中,还需要给偏置赋值小的非零值来避免死亡神经元
W1 = tf.Variable(tf.truncated_normal([in_units, h1_units], stddev=0.1))
b1 = tf.Variable(tf.zeros([h1_units]))
W2 = tf.Variable(tf.zeros([h1_units, 10]))
b2 = tf.Variable(tf.zeros([10]))
# 定义输入x的placeholder,由于Dropout的比率keep_prob在测试和训练时不一样,训练时小于1,预测时大于1
# keep_prob训练时小于1,用以制造随机性,防止过拟合;预测时大于1,即使用全部特征来预测样本的类别
# 所以也把Dropout的比率keep_prob作为计算图的输入,并定义成一个placeholder
x = tf.placeholder(tf.float32, [None, in_units])
keep_prob = tf.placeholder(tf.float32) # 保留节点的概率(保留数据而不置0的比例)
# 建立隐藏层和输出层,并且调用Dropout函数处理隐含层输出数据
# ReLU的优点:单侧抑制,相对宽阔的兴奋边界,稀疏激活性
# 隐含层的激活函数用ReLU可以提高训练速度和模型准确率
hidden1 = tf.nn.relu(tf.matmul(x, W1) + b1) # 隐含层激活函数为ReLU
hidden1_drop = tf.nn.dropout(hidden1, keep_prob) # 实现Dropout的功能,即随机将一部分节点置为0
y = tf.nn.softmax(tf.matmul(hidden1_drop, W2) + b2) # 输出层,shape和y_一样,[None, 10]
# 定义损失函数cross_entropy,并指定自适应优化器Adagrad优化损失函数
# y_和y是相同的维度[None, 10],两者相乘,实质求内积,求和按照[1]列求和(一个样本的所有类别求和),求和后为一维向量,平均后为1个数
y_ = tf.placeholder(tf.float32, [None, 10])
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))
train_step = tf.train.AdagradOptimizer(0.3).minimize(cross_entropy)
tf.global_variables_initializer().run()
# 由于加入隐含层,需要更多的训练迭代来优化模型参数达到一个比较好的效果
# 进行训练3000个batch,每个batch有100个样本,一共30万的样本,相当于对全数据进行5轮迭代
for i in range(3000):
batch_xs, batch_ys = mnist.train.next_batch(100)
train_step.run({x: batch_xs, y_: batch_ys, keep_prob: 0.75})
# 对模型进行准确性评测,其中加入了keep_prob=1
# tf.cast是将correct_prediction输出的bool值转换为float32
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print(accuracy.eval({x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))
# 0.9778
最终我们再测试集上可以达到98%的准确率,相比于Softmax,我们的误差由8%降到了2%。
多层神经网络依靠隐藏层,可以组合出高阶特征,比如横线、竖线、圆圈等,之后可以将这个高阶特征再组合成数字,实现精确的匹配和分类。隐藏层输出的高阶特征经常是可以复用的,所以每一类的判别、概率输出都共享这些高阶特征,而不是各自连接独立的高阶特征。
我们也可以发现,新增一个隐藏层,并使用了Dropout、Adagrad和ReLU,而代码并没有增加很多,这就是TensorFlow的优势。它的代码非常简洁,没有太多冗余,可以方便的将有用的模块拼装在一起。
当然使用全连接的深度神经网络也是有局限的,即使我们使用很深的网络、很多隐藏节点、进行很多次迭代,也很难在MNIST数据集上获得99%以上的准确率。这时就该卷积神经网络(CNN)出场了。
model3:输入层→卷积层1→卷积层2→全连接→dropout层→全连接→输出层softmax
卷积神经网络CNN
特点:
- 卷积的权值共享结构,可以大幅减少神经网络的参数量,防止过拟合的同时又降低了神经网络的复杂度。
- CNN训练的模型对缩放,平移,旋转等畸变具有不变性,泛化性强。
- 降低图像预处理的要求,避免复杂的特征工程
- 首个可进行多层训练的网络结构(全连接不行,因为有参数过多,梯度弥散问题)
CNN一般由多个卷积层构成,卷积层操作:
- 图像通过多个不同的卷积核的滤波,并加偏置(bias),提取局部特征,每个卷积核会映射出一个新的2D图像。
- 将卷积核的输出结果,进行非线性的激活函数(ReLU最常用)处理。
- 对激活函数的结果再进行池化操作,即降采样,一般采用最大池化方法,保留最显著的特征,并提升模型的畸变容错能力。
权值共享解释:
- 一个卷积核对应一个新图像,新图像的每个像素来自相同的卷积核,这就是权值共享
- 参数量只和卷积核大小有无,与多少隐含节点和图片有多大无关。
CNN要点:
局部连接,权值共享,池化层的降采样(赋予模型轻度形变的容忍性,提高了模型泛化能力)
代码: 两个卷积层加一个全连接层构建一个简单但非常有代表性的卷积神经网络。
"""
作者:Heart Sea
功能:基于minist, CNN实现识别手写数字
Model:
输入层, 1D转换2D
卷积层, 卷积, 激活relu, 最大池化
卷积层, 卷积, 激活relu, 最大池化
全连接, 2D转换1D, 激活relu
隐藏层(Dropout层)
全连接, softmax
输出层
版本:3.0
日期:10/11/2019
"""
from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
sess = tf.InteractiveSession()
# 由于使用ReLU
# 需要使用正态分布给参数加噪声(这里加入截断的正态分布噪声),来打破完全对称并且避免0梯度
# 还需要给偏置赋值小的非零值来避免死亡神经元
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
# 定义卷积层函数,strides代表卷积模板移动的步长,都是1表示划过图片每一个点
# padding表示边界处理方式,SAME让卷积的输入和输出保持同样的尺寸
# x是输入,w卷积的参数
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
# 定义最大池化函数,ksize参数是滤波器大小,表示2*2的滤波器,
# strides设为横竖两个方向以2为步长,步长如果为1,得到一个尺寸不变的图片
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# CNN会利用到空间的结构信息,需要将1D转换成2D
# 利用tf.reshape函数对输入的一维向量还原为28x28的结构,-1代表样本数量不固定,最后1代表颜色通道数量
# x特征,y_真实的label
x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])
x_image = tf.reshape(x, [-1, 28, 28, 1])
# 定义第一个卷积层,[5, 5, 1, 32]代表 卷积核尺寸为5x5,1个通道,32个不同卷积核
# 对权重、偏置初始化,然后经卷积层和激活函数激活,最后池化操作
# h_pool1尺寸:14*14*32
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
# 定义第二个卷积层,64是卷积核的数量,提取64种特征
# h_pool2尺寸:7*7*64(经过两次池化)
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
# 经过两层池化,边长变为7*7,所以第二个卷积层输出的tensor尺寸为7*7*64
# 全连接层处理
# h_fc1尺寸:1*1024
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
# 减轻过拟合,使用Dropout层
# h_fc1尺寸:1*1024
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
# 建立Softmax层与Dropout层连接,最后输出概率
# y_conv尺寸:1*10
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
# 定义损失函数,指定Adam优化器优化
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y_conv), reduction_indices=[1]))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
# 计算分类准确率
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
tf.global_variables_initializer().run()
# 开始训练,训练2万次,mini_batch为50,每100次显示分类精度
# 评测时,keep_prob设为1,用以实时监测模型性能
for i in range(20000):
batch = mnist.train.next_batch(50)
if i % 100 == 0:
train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0})
print("step %d, training accuracy %g" % (i, train_accuracy))
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
# 对测试集上进行测试
print("test accuracy %g" % accuracy.eval(feed_dict={x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))
# 99.2%
step 0, training accuracy 0.1
step 100, training accuracy 0.88
。
。
。
这个简单的卷积神经网络模型的准确率大约为99.2%,基本可以满足对手写数字识别准确率的要求。相比之前的深度神经网络2%的错误率,CNN的错误率下降了60%。这其中主要的性能提升都来自更优秀的网络模型设计,充分说明卷积网络对图像特征的提取和抽象能力。依靠卷积核的权值共享,CNN的参数数量并没有爆炸,降低计算量的同时也减轻了过拟合,整个模型的性能有着较大的提升。