二叉堆(最小堆, 最大堆)介绍与实现

二叉堆是一种特殊的二叉树, 它总是保证一棵树的最小元素(最小堆)或者最大元素(最大堆)处于树根上, 常见的应用场景就是用于构建优先队列, 在jdk中Doug Lea所实现的ScheduledThreadPoolExecutor中就用到了最小堆;

---

• 二叉堆介绍
• 二叉堆的编程实现
• 应用场景

二叉堆介绍

什么是树？

计算机中树是一种数据结构(有向无环图), 因为它看起来像一颗倒挂的树, 所以被称为树。在计算机中对现实世界中的事物进行模拟与呈现, 树类型数据结构被应用在很多地方,
比如一个国家的行政区域划分

国家–>省—>市—>县—>乡—>镇—>村—>组

再如一个学校里学生的组织结构,

学校—>年级—>班级—>小组—>组成员

树里面的二叉树

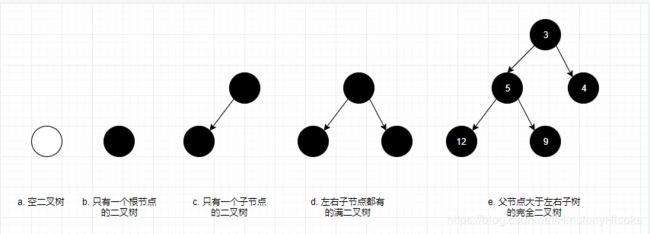
• 二叉树是树中的一类, 它里面要求每个父节点最多只能有两个子节点(左和右);
• 满二叉树指除了叶结点外树中其他每一个结点都有左右子叶且叶子结点都处在最底层的二叉树;
• 完全二叉树则要比满二叉树规则松一点, 指若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布, 一颗满二叉树也一定是完全二叉树；
• 二叉堆就是在完全二叉树的规则之上再约定, 每个父节点一定比其左右子节点的值要小(最小堆)/大(最大堆)；

下面画图举例二叉堆的数据规则:

二叉堆的编程实现

算法实现

这里以最小堆为例讲解算法

假设这里要将一组无序整数构建到一棵最小堆里面去; {3, 5, 9, 1, 10, 8, 2, 12, 7, 4}
算法说明：首先最小堆的特性有, 规则一堆顶(二叉堆的根节点)为此堆中最小元素, 规则二每个节点的值大于其左右两节点的值, 针对同一组被构建的数据集合, 第一点规则下来, 确保跟节点的元素必定是固定的某一个值, 但是第二个规则下, 除了跟节点外的其他节点可能不同的构建算法最后得到的树是不一样的(具体哪个元素在哪个节点上); 规则二下, 我们发现树的左右子节点是无差别的;

1. 初始态堆中无元素, 当放入第一个节点时, 自然是放到堆顶(跟节点);
   
2. 继续放入第二个元素, 为了保证堆顶元素最小, 我们就用要放入的元素和堆顶元素比较, 如果比它小, 那就占了堆顶位置, 将原来的堆顶元素拿出来往下比较移动, 这里自然就是放在跟节点的左子树, 如果比它大, 那就直接把第二个元素放到左子树;
   
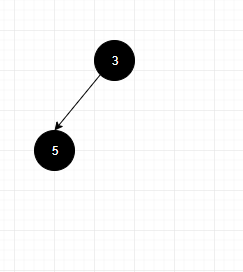
3. 接下来准备放入第三个元素, 现在我们要思考一个问题, 是从堆顶开始比较还是堆底呢?
   分析一下: 因为我们每插入一个元素都要保证树是完全二叉树, 这里我们先从堆顶以广度搜索的方式进行比较放入, 把腰放入的新元素和比较路径上的元素进行依次比较, 碰到比自己小的元素, 就进行置换, 直到比较至最后一个元素, 然后进行树的分支添加;
   
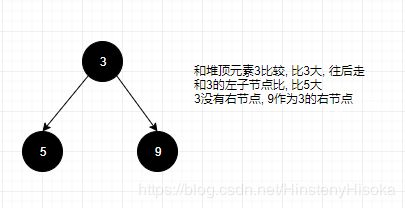
4. 继续放入第四个元素
   
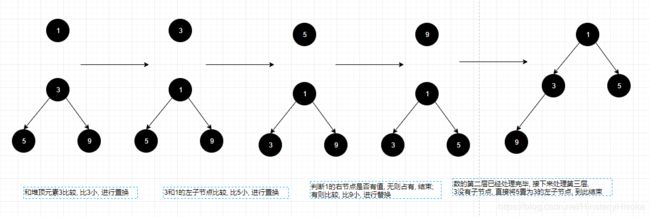
5. 不断放入元素, 直至最后一个;
   
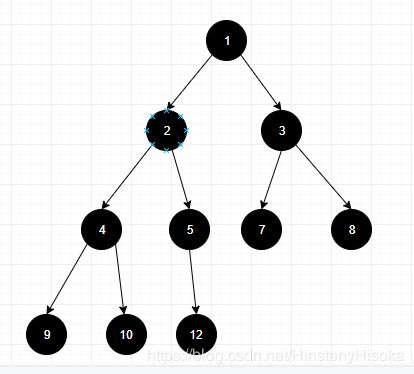
   思考: 这个插入构建堆的算法时间复杂度为(O2), 效率有点低, 而且我们可以发现最后构成的堆, 太规则了, 实现了全堆排序, 做了很多无用功呀, 下面我们用java代码实现一个从堆底比较插入的构建算法, 算法复杂度为(log2N);

这里使用java语言实现，如下

将上面的二叉堆构建算法用编程语言实现时, 这里我们使用数组作为堆的底层数据结构, 转化与映射关系如下

1. 堆的插入, 需要保持堆特性, 从堆底最后一个元素的父节点开始比较, 进行替换, 依次向上直到父节点
   (这里采用数组的数据结构, 我们的比较插入会天然形成一棵完全二叉树, 就比上面算法中为了保证完全树结构高效);

    /**
     * add one element to heap
     *
     * @param e element
     * @return add result
     */
    private boolean addToHeap(E e) {
        final ReentrantLock lock = this.lock;
        lock.lock();
        try {
            if (this.size == heaps.length) {
                heaps = grow();
            }
            siftUp(size++, e);
            return true;
        } finally {
            lock.unlock();
        }
    }
    /**
     * Sifts element added at bottom up to its heap-ordered spot.
     *
     * @param k bottom index
     * @param item to bo moving
     */
    private void siftUp(int k, E item) {
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            E e = (E) heaps[parent];
            if (compareTo(item, e) >= 0) {
                break;
            }
            heaps[k] = e;
            k = parent;
        }
        heaps[k] = item;
    }

2. 弹出堆顶元素, 将最后一个元素从堆顶开始依次往下沉, 放置合适的位置(因为二叉堆只规定父节点比左右子节点大(小), 所以我们不用考虑左右子节点之间的大小, 直接找到一个比当前元素小的地方放置它);

    /**
     * remove element from heap
     *
     * @param x to be remove
     * @return remove result
     */
    private boolean remove(E x) {
        final ReentrantLock lock = this.lock;
        lock.lock();
        try {
            int i = indexOf(x);
            if (i < 0) {
                return false;
            }
            int s = --size;
            E replacement = (E) heaps[s];
            heaps[s] = null;
            if (s != i) {
                siftDown(i, replacement);
                if (heaps[i] == replacement) {
                    siftUp(i, replacement);
                }
            }
            return true;
        } finally {
            lock.unlock();
        }
    }

    /**
     * Sifts element added at top down to its heap-ordered spot. Call only when holding lock.
     *
     * @param k start index for siftDown
     * @param item the item to be sift
     */
    private void siftDown(int k, E item) {
        int half = size >>> 1;
        while (k < half) {
            int child = (k << 1) + 1;
            E c = (E) heaps[child];
            int right = child + 1;
            if (right < size && compareTo(c, (E) heaps[right]) > 0) {
                c = (E) heaps[child = right];
            }
            if (compareTo(item, c) <= 0) {
                break;
            }
            heaps[k] = c;
            k = child;
        }
        heaps[k] = item;
    }

3. 使用二叉堆进行堆排序

    /**
     * sort the heap by HeapSort
     *
     * @return the top of element
     */
    public List sort() {
        return size > 0 ? sort(false) : null;
    }

    /**
     * sort the heap by HeapSort
     *
     * @param newHeap if use newHeap for use less time
     * @return sort arrays
     */
    private List sort(boolean newHeap) {
        final ReentrantLock lock = this.lock;
        lock.lock();
        try {
            if (size <= 0) {
                return null;
            }
            Object[] newHeaps = newHeap ? Arrays.copyOf(heaps, size) : heaps;
            int heapSize = this.size;
            for (int i = 0; size-- > 0; i++) {
                Object top = heaps[0];
                heaps[0] = heaps[size];
                siftDown(0, (E) heaps[0]);
                if (newHeap) {
                    newHeaps[i] = top;
                } else {
                    newHeaps[size] = top;
                }
            }
            this.size = heapSize;
            if (!newHeap) {
                // not use new-heap in sort, so we need to do a reverse
                for (int i = 0, j = this.size >>> 1, k = this.size - 1; i < j; i++) {
                    Object temporary = newHeaps[i];
                    newHeaps[i] = newHeaps[k - i];
                    newHeaps[k - i] = temporary;
                }
            }
            return Arrays.asList(newHeaps).stream().map(item -> (E) item).collect(Collectors.toList());
        } finally {
            lock.unlock();
        }
    }

4. 单元测试一下

    @Test(testName = "测试使用二叉堆示例")
    public void testAesUtilEncryptAndDecryptToStr() {
        // 构建一个二叉堆, 内部存放int数据
        Integer[] data = {3, 5, 9, 1, 10, 8, 2, 12, 7, 4};
        System.out.println("============== 最小堆示例 ==============");
        BinaryHeap heap = new BinaryHeap();
        for (int i = 0; i < data.length; i++) {
            heap.add(data[i]);
        }
        System.out.println(heap);
        System.out.println("============== 最小堆构建好了, 现在依次弹出堆顶元素, 再看堆中数据排布 ==============");
        while (heap.size() > 0) {
            heap.popTop();
            System.out.println(heap);
        }
        System.out.println("============== 最大堆示例 ==============");
        heap = new BinaryHeap(true);
        for (int i = 0; i < data.length; i++) {
            heap.add(data[i]);
        }
        System.out.println(heap);
        System.out.println("============== 最大堆构建好了, 现在依次弹出堆顶元素, 再看堆中数据排布 ==============");
        while (heap.size() > 0) {
            heap.popTop();
            System.out.println(heap);
        }
        System.out.println("============== 堆排序示例 ==============");
        heap = new BinaryHeap();
        for (int i = 0; i < data.length; i++) {
            heap.add(data[i]);
        }
        List sort = heap.sort();
        System.out.println(sort);
    }

5. 单元测试输出

============== 最小堆示例 ==============
BinaryHeap{heaps=[1, 3, 2, 5, 4, 9, 8, 12, 7, 10]}
============== 最小堆构建好了, 现在依次弹出堆顶元素, 再看堆中数据排布 ==============
BinaryHeap{heaps=[2, 3, 8, 5, 4, 9, 10, 12, 7]}
BinaryHeap{heaps=[3, 4, 8, 5, 7, 9, 10, 12]}
BinaryHeap{heaps=[4, 5, 8, 12, 7, 9, 10]}
BinaryHeap{heaps=[5, 7, 8, 12, 10, 9]}
BinaryHeap{heaps=[7, 9, 8, 12, 10]}
BinaryHeap{heaps=[8, 9, 10, 12]}
BinaryHeap{heaps=[9, 12, 10]}
BinaryHeap{heaps=[10, 12]}
BinaryHeap{heaps=[12]}
BinaryHeap{heaps=[]}
============== 最大堆示例 ==============
BinaryHeap{heaps=[12, 10, 8, 9, 4, 5, 2, 1, 7, 3]}
============== 最大堆构建好了, 现在依次弹出堆顶元素, 再看堆中数据排布 ==============
BinaryHeap{heaps=[10, 9, 8, 7, 4, 5, 2, 1, 3]}
BinaryHeap{heaps=[9, 7, 8, 3, 4, 5, 2, 1]}
BinaryHeap{heaps=[8, 7, 5, 3, 4, 1, 2]}
BinaryHeap{heaps=[7, 4, 5, 3, 2, 1]}
BinaryHeap{heaps=[5, 4, 1, 3, 2]}
BinaryHeap{heaps=[4, 3, 1, 2]}
BinaryHeap{heaps=[3, 2, 1]}
BinaryHeap{heaps=[2, 1]}
BinaryHeap{heaps=[1]}
BinaryHeap{heaps=[]}
============== 堆排序示例 ==============
[1, 2, 3, 4, 5, 7, 8, 9, 10, 12]

应用场景

堆排序

堆排序可以, 我们可以把堆顶元素挪到堆的最后一个元素位置, 然后将前面n-1个元素重新构建堆, 如此反复, 就能形成一个有序的堆;

优先队列

在jdk中有一个定时调度线程池, 它的内部便是采用一个最小堆保存需要被调度执行的任务, 堆顶便是未来最先需要被调度的任务, 插入和弹出操作都需要维护堆的有效性, 都需要加同步锁,;

注:

1. 一棵树当中没有子结点（即度为0）的结点称为叶子结点，简称“叶子”。 叶子是指度为0的结点，又称为终端结点。
2. 全部代码见: commons