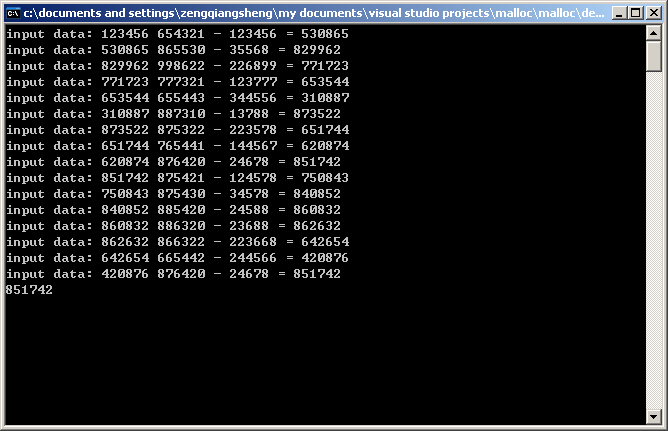
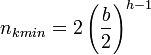Is Natural Number N Powered

make judge on a natural number: if it's equals to pow(x, 2) and x is a natural number too.

bool isPowered2( int n, int low, int hig, int dvd)
{
     int mid = (low + hig) / dvd;
     int pwr = mid * mid;
     if (pwr == n) return true ;
     else if (low == hig) return false ;

     if (pwr > n) { // target number is in [low, mid-1]
         return isPowered2(n, low, mid - 1 , dvd);
    }

     if (pwr < n) { // target number is in [mid+1, hig]
         return isPowered2(n, mid + 1 , hig, 2 ); // use binary searching here.
    }
}

bool isPowered( int n)
{
     if (n <= 100 ) {
         if (n <= 25 )
             if (n == 1 || n == 4 || n == 9 || n == 16 || n == 25 ) return true ;
         if (n == 36 || n == 49 || n == 64 || n == 81 || n == 100 ) return true ;
         else return false ;
    }

     return isPowered2(n, 1, n-1, 10); // why use 10 here ?
}

posted @ 2010-12-07 10:50 JonsenElizee 阅读(33) | 评论 (0) | 编辑收藏

IPC waitpid

#include < sys / types.h >
#include < sys / wait.h >

pid_t waitpid(pid_t pid, int * status, int options);

pid < - 1 wait for any process with group id value = - pid;
pid = - 1 same as wait();
pid = 0 wait for any subprocess of this process;
pid > 0 wait for process with it ' s id = pid;

options = 0 don ' t use options;
    WNOHANG  : just return if no subprocess finished.
    WUNTRACED: just return if subprocess is hanged up now.

status the return status of subprocess is stored in this int value.
    to make sure what happed, we can use following macro:
    WIFEXITED(status)      如果子进程正常结束则为非0值。
    WEXITSTATUS(status)    取得子进程exit()返回的结束代码,一般会先用WIFEXITED来判断是否正常结束才能使用此宏。
    WIFSIGNALED(status)    如果子进程是因为信号而结束则此宏值为真
    WTERMSIG(status)       取得子进程因信号而中止的信号代码,一般会先用WIFSIGNALED来判断后才使用此宏。
    WIFSTOPPED(status)     如果子进程处于暂停执行情况则此宏值为真。一般只有使用WUNTRACED时才会有此情况。
    WSTOPSIG(status)       取得引发子进程暂停的信号代码,一般会先用WIFSTOPPED来判断后才使用此宏。

return pid the subprocess id, else - 1 for error, and errno is set .

posted @ 2010-12-02 15:28 JonsenElizee 阅读(31) | 评论 (0) | 编辑收藏

B+Tree

B+ tree

From Wikipedia, the free encyclopedia

Jump to: navigation, search

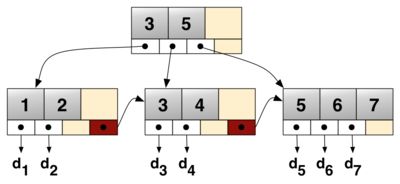
A simple B+ tree example linking the keys 1–7 to data values d ₁-d ₇. The linked list (red) allows rapid in-order traversal.

In computer science, a B+ tree or B plus tree is a type of treewhich represents sorted data in a way that allows for efficientinsertion, retrieval and removal of records, each of which is identifiedby a key. It is a dynamic, multilevel index, with maximum andminimum bounds on the number of keys in each index segment (usuallycalled a "block" or "node"). In a B+ tree, in contrast to a B-tree, all records are stored at the leaf level of the tree; only keys are stored in interior nodes.

The primary value of a B+ tree is in storing data for efficient retrieval in a block-oriented storage context—in particular, filesystems. This is primarily because unlike binary search trees,B+ trees have very high fanout (typically on the order of 100 or more),which reduces the number of I/O operations required to find an elementin the tree.

NTFS, ReiserFS, NSS, XFS, and JFS filesystems all use this type of tree for metadata indexing. Relational database management systems such as IBM DB2^[1], Informix^[1], Microsoft SQL Server^[1], Oracle 8^[1], Sybase ASE^[1], PostgreSQL^[2], Firebird, MySQL^[3] and SQLite^[4] support this type of tree for table indices. Key-value database management systems such as CouchDB^[5], Tokyo Cabinet^[6] and Tokyo Tyrant support this type of tree for data access. InfinityDB^[7] is a concurrent BTree.

[edit] Details

The order, or branching factor b of a B+ tree measures thecapacity of nodes (i.e. the number of children nodes) for internal nodesin the tree. The actual number of children for a node, referred to hereas m, is constrained for internal nodes so that 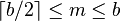$\lceil b/2 \rceil \le m \le b$ . The root is an exception: it is allowed to have as few as two children. For example, if the order of a B+ tree is 7, each internal node(except for the root) may have between 4 and 7 children; the root mayhave between 2 and 7. Leaf nodes have no children , but are constrainedso that the number of keys must be at least 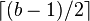$\lceil (b-1)/2 \rceil$ and at most b − 1.In the situation where a B+ tree is nearly empty, it only contains onenode, which is a leaf node. (The root is also the single leaf, in thiscase.) This node is permitted to have as little as one key if necessary.

[edit] Search

The algorithm to perform a search for a record r follows pointers tothe correct child of each node until a leaf is reached. Then, the leafis scanned until the correct record is found (or until failure).

  function search(record r)
    u := root
    while (u is not a leaf) do
      choose the correct pointer in the node
      move to the first node following the pointer
      u := current node
    scan u for r

This pseudocode assumes that no repetition is allowed.

[edit] Insertion

Perform a search to determine what bucket the new record should go in.

if the bucket is not full, add the record.
otherwise, split the bucket.
- allocate new leaf and move half the bucket's elements to the new bucket
- insert the new leaf's smallest key and address into the parent.
- if the parent is full, split it also
  - add the middle key to the parent node
- repeat until a parent is found that need not split
if the root splits, create a new root which has one key and two pointers.

[edit] Characteristics

For a b-order B+ tree with h levels of index:

The maximum number of records stored is n_max = b^h − b^{h − 1}
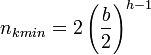
The minimum number of keys is $n_{kmin} = 2\left(\frac{b}{2}\right)^{h-1}$
The space required to store the tree is O(n)
Inserting a record requires O(log_bn) operations in the worst case
Finding a record requires O(log_bn) operations in the worst case
Removing a (previously located) record requires O(log_bn) operations in the worst case
Performing a range query with k elements occurring within the range requires O(log_bn + k) operations in the worst case.

[edit] Implementation

The leaves (the bottom-most index blocks) of the B+ tree are often linked to one another in a linked list; this makes range queriesor an (ordered) iteration through the blocks simpler and more efficient(though the aforementioned upper bound can be achieved even withoutthis addition). This does not substantially increase space consumptionor maintenance on the tree. This illustrates one of the significantadvantages of a B+-tree over a B-tree;in a B-tree, since not all keys are present in the leaves, such anordered linked list cannot be constructed. A B+-tree is thusparticularly useful as a database system index, where the data typicallyresides on disk, as it allows the B+-tree to actually provide anefficient structure for housing the data itself (this is described in ^[8] as index structure "Alternative 1").

If a storage system has a block size of B bytes, and the keys to be stored have a size of k, arguably the most efficient B+ tree is one where b = (B / k) − 1.Although theoretically the one-off is unnecessary, in practice there isoften a little extra space taken up by the index blocks (for example,the linked list references in the leaf blocks). Having an index blockwhich is slightly larger than the storage system's actual blockrepresents a significant performance decrease; therefore erring on theside of caution is preferable.

If nodes of the B+ tree are organized as arrays of elements, then itmay take a considerable time to insert or delete an element as half ofthe array will need to be shifted on average. To overcome this problem,elements inside a node can be organized in a binary tree or a B+ treeinstead of an array.

B+ trees can also be used for data stored in RAM. In this case areasonable choice for block size would be the size of processor's cache line.However, some studies have proved that a block size a few times largerthan the processor's cache line can deliver better performance if cache prefetching is used.

Space efficiency of B+ trees can be improved by using some compression techniques. One possibility is to use delta encodingto compress keys stored into each block. For internal blocks, spacesaving can be achieved by either compressing keys or pointers. Forstring keys, space can be saved by using the following technique:Normally the ith entry of an internal block contains the firstkey of block i+1. Instead of storing the full key, we could store theshortest prefix of the first key of block i+1 that is strictly greater(in lexicographic order) than last key of block i. There is also asimple way to compress pointers: if we suppose that some consecutiveblocks i, i+1...i+k are stored contiguously, then it will suffice tostore only a pointer to the first block and the count of consecutiveblocks.

All the above compression techniques have some drawbacks. First, afull block must be decompressed to extract a single element. Onetechnique to overcome this problem is to divide each block intosub-blocks and compress them separately. In this case searching orinserting an element will only need to decompress or compress asub-block instead of a full block. Another drawback of compressiontechniques is that the number of stored elements may vary considerablyfrom a block to another depending on how well the elements arecompressed inside each block.

[edit] History

The B tree was first described in the paper Organization and Maintenance of Large Ordered Indices. Acta Informatica 1: 173–189 (1972) by Rudolf Bayerand Edward M. McCreight. There is no single paper introducing the B+tree concept. Instead, the notion of maintaining all data in leaf nodesis repeatedly brought up as an interesting variant. An early survey of Btrees also covering B+ trees is Douglas Comer: "The Ubiquitous B-Tree",ACM Computing Surveys 11(2): 121–137 (1979). Comer notes that the B+tree was used in IBM's VSAM data access software and he refers to an IBMpublished article from 1973.

[edit] See also

Binary Search Tree
B# Tree
B-tree
Bitmap index
Divide and conquer algorithm

[edit] References

^ ^a ^b ^c ^d ^e Ramakrishnan Raghu, Gehrke Johannes - Database Management Systems, McGraw-Hill Higher Education (2000), 2nd edition (en) page 267
^ PostgreSQL documentation
^ Colin Charles Agenda - Morning sessions at MySQL MiniConf
^ SQLite Version 3 Overview
^ CouchDB Guide (see note after 3rd paragraph)
^ Tokyo Cabinet reference
^ The Design Of The InfinityDB Database Engine
^ Ramakrishnan, R. and Gehrke, J. Database Management Systems, McGraw-Hill Higher Education (2002), 3rd edition

[edit] External links

Wikibooks has a book on the topic of

Transwiki:B+ tree

B+ tree in Python, used to implement a list
B+ tree implementation as C++ template library
Dr. Monge's B+ Tree index notes
Open Source C++ B+ Tree Implementation
Interactive B+ Tree Implementation in C
Open Source Javascript B+ Tree Implementation
Perl implementation of B+ trees
java/C#/python implementations of B+ trees
Evaluating the performance of CSB+-trees on Mutithreaded Architectures
Effect of node size on the performance of cache conscious B+-trees
Fractal Prefetching B+-trees
Towards pB+-trees in the field: implementations Choices and performance
Cache-Conscious Index Structures for Main-Memory Databases
Cache Oblivious B(+)-trees
The Power of B-Trees: CouchDB B+ Tree Implementation

posted @ 2010-12-01 11:48 JonsenElizee 阅读(484) | 评论 (0) | 编辑收藏

R-Tree

R-tree

From Wikipedia, the free encyclopedia

Jump to: navigation, search

This article is about the data structure. For the type of metric space, see Real tree.

Simple example of an R-tree for 2D rectangles

Visualization of an R*-tree for 3D cubes using ELKI

R-trees are tree data structures that are similar to B-trees, but are used for spatial access methods,i.e., for indexing multi-dimensional information; for example, the (X,Y) coordinates of geographical data. A common real-world usage for anR-tree might be: "Find all museums within 2 kilometres (1.2 mi) of mycurrent location".

The data structure splits space with hierarchically nested, and possibly overlapping, minimum bounding rectangles (MBRs, otherwise known as bounding boxes, i.e. "rectangle", what the "R" in R-tree stands for).

Each node of an R-tree has a variable number of entries (up to some pre-defined maximum). Each entry within a non-leaf node stores two pieces of data: a way of identifying a child node, and the bounding box of all entries within this child node.

The insertion and deletion algorithms use the bounding boxes from thenodes to ensure that "nearby" elements are placed in the same leaf node(in particular, a new element will go into the leaf node that requiresthe least enlargement in its bounding box). Each entry within a leafnode stores two pieces of information; a way of identifying the actualdata element (which, alternatively, may be placed directly in the node),and the bounding box of the data element.

Similarly, the searching algorithms (e.g., intersection,containment, nearest) use the bounding boxes to decide whether or notto search inside a child node. In this way, most of the nodes in thetree are never "touched" during a search. Like B-trees, this makesR-trees suitable for databases, where nodes can be paged to memory when needed.

Different algorithms can be used to split nodes when they become too full, resulting in the quadratic and linear R-tree sub-types.

R-trees do not historically guarantee good worst-case performance, but generally perform well with real-world data.^{[citation needed]} However, a new algorithm was published in 2004 that defines the Priority R-Tree, which claims to be as efficient as the most efficient methods of 2004 and is at the same time worst-case optimal.^[1]

When data is organized in an R-Tree, the k nearest neighbors (for any L^p-Norm) of all points can efficiently be computed using a spatial join^[2]. This is beneficial for many algorithms based on the k nearest neighbors, for example the Local Outlier Factor.

[edit] Variants

R* tree
R+ tree
Hilbert R-tree
Priority R-Tree (PR-Tree) - The PR-tree performs similarly to the best known R-tree variants on real-life and relatively evenly distributed data, but outperforms them significantly on more extreme data.^[1]

[edit] Algorithm

[edit] Search

The input is a search rectangle (Query box). Searching is quite similar to searching in a B+tree.The search starts from the root node of the tree. Every internal nodecontains a set of rectangles and pointers to the corresponding childnode and every leaf node contains the rectangles of spatial objects (thepointer to some spatial object can be there). For every rectangle in anode, it has to be decided if it overlaps the search rectangle or not.If yes, the corresponding child node has to be searched also. Searchingis done like this in a recursive manner until all overlapping nodes havebeen traversed. When a leaf node is reached, the contained boundingboxes (rectangles) are tested against the search rectangle and theirobjects (if there are any) are put into the result set if they liewithin the search rectangle.

[edit] Insertion

To insert an object, the tree is traversed recursively from the rootnode. All rectangles in the current internal node are examined. Theconstraint of least coverage is employed to insert an object, i.e., thebox that needs least enlargement to enclose the new object is selected.In the case where there is more than one rectangle that meets thiscriterion, the one with the smallest area is chosen. Inserting continuesrecursively in the chosen node. Once a leaf node is reached, astraightforward insertion is made if the leaf node is not full. If theleaf node is full, it must be split before the insertion is made. A fewsplitting algorithms have been proposed for good R-tree performance.

This section requires expansion.

[edit] Bulk-loading

Sort-Tile-Recursive (STR) ^[3]
Packed Hilbert R-Tree - Uses the Hilbert value of the center of a rectangle to sort the leaf nodes and recursively builds the tree.
Nearest-X - Rectangles are sorted on the x-coordinate and nodes are created.

This section requires expansion.

[edit] See also

Segment tree
Interval tree - A degenerate R-Tree for 1 dimension (usually time).
Bounding volume hierarchy
Spatial index
GiST

[edit] References

^ ^a ^b Lars Arge, Mark de Berg, Herman J. Haverkort, Ke Yi: ""The Priority R-Tree: A Practically Efficient and Worst-Case Optimal RTree"", SIGMOD 2004, June 13–18, Paris, France
^ Brinkhoff, T.; Kriegel, H. P.; Seeger, B. (1993). "Efficient processing of spatial joins using R-trees". ACM SIGMOD Record 22: 237. doi:10.1145/170036.170075. edit
^ Scott T. Leutenegger, Jeffrey M. Edgington and Mario A. Lopez: STR: A Simple and Efficient Algorithm for R-Tree Packing

Antonin Guttman: R-Trees: A Dynamic Index Structure for Spatial Searching, Proc. 1984 ACM SIGMOD International Conference on Management of Data, pp. 47–57. ISBN 0-89791-128-8
Yannis Manolopoulos, Alexandros Nanopoulos, Apostolos N. Papadopoulos, Yannis Theodoridis: R-Trees: Theory and Applications, Springer, 2005. ISBN 1-85233-977-2
N. Beckmann, H.-P. Kriegel, R. Schneider, B. Seeger: The R*-Tree: An Efficient and Robust Access Method for Points and Rectangles. SIGMOD Conference 1990: 322-331

[edit] External links

R-tree portal
R-Tree implementations: C & C++, Java applet, Common Lisp, Python, Javascript.

[hide] v • d • e Trees in computer science

Binary trees	Binary search tree (BST) · Van Emde Boas tree · Cartesian tree · Top Tree · T-tree

Self-balancing binary search trees	Red-black tree · AVL tree · AA tree · Splay tree · Scapegoat tree · Treap

B-trees	B+ tree · B*-tree · UB-tree · 2-3 tree · 2-3-4 tree · (a,b)-tree · Dancing tree · Htree · B ^x-tree

Tries	Suffix tree · Radix tree · Ternary search tree

Binary space partitioning (BSP) trees	Quadtree · Octree · kd-tree ( implicit) · VP-tree

Non-binary trees	Exponential tree · Fusion tree · Interval tree · PQ tree · Range tree · SPQR tree

Spatial data partitioning trees	*R-tree · R+ tree · R tree · X-tree · M-tree · Segment tree · Fenwick tree · Hilbert R-tree**

Other trees	Heap · Hash tree · Finger tree · Metric tree · Cover tree · BK-tree · Doubly-chained tree · iDistance

Retrieved from " http://en.wikipedia.org/wiki/R-tree"

Categories: R-tree | Database index techniques

posted @ 2010-12-01 11:46 JonsenElizee 阅读(560) | 评论 (0) | 编辑收藏

HOW TO CONNECT APACHE AND TOMCAT

简介： 整合 Apache Http Server 和 Tomcat 可以提升对静态文件的处理性能、利用 Web 服务器来做负载均衡以及容错、无缝的升级应用程序。本文介绍了三种整合 Apache 和 Tomcat 的方式

Author LiuDong

首先我们先介绍一下为什么要让 Apache 与 Tomcat 之间进行连接。事实上 Tomcat 本身已经提供了 HTTP服务，该服务默认的端口是 8080，装好 tomcat 后通过 8080 端口可以直接使用 Tomcat 所运行的应用程序，你也可以将该端口改为80。

既然 Tomcat 本身已经可以提供这样的服务，我们为什么还要引入 Apache 或者其他的一些专门的 HTTP 服务器呢？原因有下面几个：

1. 提升对静态文件的处理性能

2. 利用 Web 服务器来做负载均衡以及容错

3. 无缝的升级应用程序

这三点对一个 web 网站来说是非常之重要的，我们希望我们的网站不仅是速度快，而且要稳定，不能因为某个 Tomcat宕机或者是升级程序导致用户访问不了，而能完成这几个功能的、最好的 HTTP 服务器也就只有 apache 的 http server 了，它跟tomcat 的结合是最紧密和可靠的。

接下来我们介绍三种方法将 apache 和 tomcat 整合在一起。

JK

这是最常见的方式，你可以在网上找到很多关于配置JK的网页，当然最全的还是其官方所提供的文档。JK 本身有两个版本分别是 1 和 2，目前 1 最新的版本是 1.2.19，而版本 2 早已经废弃了，以后不再有新版本的推出了，所以建议你采用版本 1。

JK 是通过 AJP 协议与 Tomcat 服务器进行通讯的，Tomcat 默认的 AJP Connector 的端口是8009。JK 本身提供了一个监控以及管理的页面 jkstatus，通过 jkstatus 可以监控 JK 目前的工作状态以及对到 tomcat的连接进行设置，如下图所示：

图 1：监控以及管理的页面 jkstatus

在这个图中我们可以看到当前JK配了两个连接分别到 8109 和 8209 端口上，目前 s2 这个连接是停止状态，而 s1这个连接自上次重启后已经处理了 47 万多个请求，流量达到 6.2 个 G，最大的并发数有 13 等等。我们也可以利用 jkstatus的管理功能来切换 JK 到不同的 Tomcat 上，例如将 s2 启用，并停用s1，这个在更新应用程序的时候非常有用，而且整个切换过程对用户来说是透明的，也就达到了无缝升级的目的。关于 JK的配置文章网上已经非常多了，这里我们不再详细的介绍整个配置过程，但我要讲一下配置的思路，只要明白了配置的思路，JK 就是一个非常灵活的组件。

JK 的配置最关键的有三个文件，分别是

httpd.conf
Apache 服务器的配置文件，用来加载 JK 模块以及指定 JK 配置文件信息

workers.properties
到 Tomcat 服务器的连接定义文件

uriworkermap.properties
URI 映射文件，用来指定哪些 URL 由 Tomcat 处理，你也可以直接在 httpd.conf 中配置这些 URI，但是独立这些配置的好处是 JK 模块会定期更新该文件的内容，使得我们修改配置的时候无需重新启动 Apache 服务器。

其中第二、三个配置文件名都可以自定义。下面是一个典型的 httpd.conf 对 JK 的配置

# (httpd.conf)
# 加载 mod_jk 模块
LoadModule jk_module modules/mod_jk.so

#
# Configure mod_jk
#

JkWorkersFile conf/workers.properties
JkMountFile conf/uriworkermap.properties
JkLogFile logs/mod_jk.log
JkLogLevel warn

接下来我们在 Apache 的 conf 目录下新建两个文件分别是 workers.properties、uriworkermap.properties。这两个文件的内容大概如下

#
# workers.properties
#


# list the workers by name

worker.list=DLOG4J, status

# localhost server 1
# ------------------------
worker.s1.port=8109
worker.s1.host=localhost
worker.s1.type=ajp13

# localhost server 2
# ------------------------
worker.s2.port=8209
worker.s2.host=localhost
worker.s2.type=ajp13
worker.s2.stopped=1

worker.DLOG4J.type=lb
worker.retries=3
worker.DLOG4J.balanced_workers=s1, s2
worker.DLOG4J.sticky_session=1

worker.status.type=status

以上的 workers.properties 配置就是我们前面那个屏幕抓图的页面所用的配置。首先我们配置了两个类型为 ajp13 的worker 分别是 s1 和 s2，它们指向同一台服务器上运行在两个不同端口 8109 和 8209 的 Tomcat上。接下来我们配置了一个类型为 lb（也就是负载均衡的意思）的 worker，它的名字是 DLOG4J，这是一个逻辑的worker，它用来管理前面配置的两个物理连接 s1 和 s2。最后还配置了一个类型为 status 的 worker，这是用来监控 JK本身的模块。有了这三个 worker 还不够，我们还需要告诉 JK，哪些 worker 是可用的，所以就有 worker.list = DLOG4J, status 这行配置。

接下来便是 URI 的映射配置了，我们需要指定哪些链接是由 Tomcat 处理的，哪些是由 Apache 直接处理的，看看下面这个文件你就能明白其中配置的意义

/*=DLOG4J
/jkstatus=status

!/*.gif=DLOG4J
!/*.jpg=DLOG4J
!/*.png=DLOG4J
!/*.css=DLOG4J
!/*.js=DLOG4J
!/*.htm=DLOG4J
!/*.html=DLOG4J

相信你已经明白了一大半了：所有的请求都由 DLOG4J 这个 worker 进行处理，但是有几个例外，/jkstatus 请求由status 这个 worker 处理。另外这个配置中每一行数据前面的感叹号是什么意思呢？感叹号表示接下来的 URI 不要由 JK进行处理，也就是 Apache 直接处理所有的图片、css 文件、js 文件以及静态 html 文本文件。

通过对 workers.properties 和 uriworkermap.properties 的配置，可以有各种各样的组合来满足我们前面提出对一个 web 网站的要求。您不妨动手试试！

回页首

http_proxy

这是利用 Apache 自带的 mod_proxy 模块使用代理技术来连接 Tomcat。在配置之前请确保是否使用的是 2.2.x 版本的 Apache 服务器。因为 2.2.x 版本对这个模块进行了重写，大大的增强了其功能和稳定性。

http_proxy 模式是基于 HTTP 协议的代理，因此它要求 Tomcat 必须提供 HTTP 服务，也就是说必须启用 Tomcat 的 HTTP Connector。一个最简单的配置如下

ProxyPass /images !
ProxyPass /css !
ProxyPass /js !
ProxyPass / http://localhost:8080/

在这个配置中，我们把所有 http://localhost 的请求代理到 http://localhost:8080/ ，这也就是Tomcat 的访问地址，除了 images、css、js 几个目录除外。我们同样可以利用 mod_proxy 来做负载均衡，再看看下面这个配置

ProxyPass /images !
ProxyPass /css ! 
ProxyPass /js !

ProxyPass / balancer://example/

BalancerMember http://server1:8080/
BalancerMember http://server2:8080/
BalancerMember http://server3:8080/

配置比 JK 简单多了，而且它也可以通过一个页面来监控集群运行的状态，并做一些简单的维护设置。

图 2：监控集群运行状态

回页首

ajp_proxy

ajp_proxy 连接方式其实跟 http_proxy 方式一样，都是由 mod_proxy 所提供的功能。配置也是一样，只需要把http:// 换成 ajp:// ，同时连接的是 Tomcat 的 AJP Connector 所在的端口。上面例子的配置可以改为：

ProxyPass /images !
ProxyPass /css ! 
ProxyPass /js !

ProxyPass / balancer://example/

BalancerMember ajp://server1:8080/
BalancerMember ajp://server2:8080/
BalancerMember ajp://server3:8080/

采用 proxy 的连接方式，需要在 Apache 上加载所需的模块，mod_proxy 相关的模块有mod_proxy.so、mod_proxy_connect.so、mod_proxy_http.so、mod_proxy_ftp.so、mod_proxy_ajp.so，其中 mod_proxy_ajp.so 只在 Apache 2.2.x 中才有。如果是采用http_proxy 方式则需要加载 mod_proxy.so 和 mod_proxy_http.so；如果是 ajp_proxy 则需要加载mod_proxy.so 和 mod_proxy_ajp.so这两个模块。

回页首

三者比较

相对于 JK 的连接方式，后两种在配置上是比较简单的，灵活性方面也一点都不逊色。但就稳定性而言就不像 JK 这样久经考验，毕竟Apache 2.2.3 推出的时间并不长，采用这种连接方式的网站还不多，因此，如果是应用于关键的互联网网站，还是建议采用 JK 的连接方式。

参考资料

获得 Apache Http Server。
获得 Apache Tomcat。
JK 文档。

关于作者

posted @ 2010-11-29 13:07 JonsenElizee 阅读(69) | 评论 (0) | 编辑收藏

Such a Nice Java Music Player

Look for this kind of nice player long long time.
It's promoted by "QianLiBingFeng" and completed at 2008/08/02 with continuing mantenance on google code web site:
http://code.google.com/p/yoyoplayer

posted @ 2010-11-25 11:44 JonsenElizee 阅读(26) | 评论 (0) | 编辑收藏

Alizee

MTV

posted @ 2010-11-12 20:04 JonsenElizee 阅读(25) | 评论 (0) | 编辑收藏

Add Dictionary Pane on Any Webpage

save this line as a url:
javascript:void((function()%20{var%20element=document.createElement('script');%20element.setAttribute('src',%20'http://dict.cn/hc/init.php');%20document.body.appendChild(element);})())

posted @ 2010-11-10 08:54 JonsenElizee 阅读(25) | 评论 (0) | 编辑收藏

Assembly Language for x86 Processors, 6th edition

Assembly Language for x86 Processors , 6th edition


*by Kip Irvine, Florida International University*
ISBN: 0-13-602212-X
Published by: Prentice-Hall (Pearson Education), February 2010
Visit the Web site for the Fifth Edition
Bookmark this Web Site

Online Resources (pearsonhighered.com)	Getting started with MASM	Chapter objectives
International Editions	Sample chapters and videos	Instructor resources
Buy at Amazon.com or Bookfinder.com	Debugging tools	Discussion group (Yahoo.com)
	Link libraries and example programs	Supplemental files
Links to Assembly Language sites	Articles
Assembly language workbook	Bug reports

New feature! This edition offers recorded videos by the author, working through solutions to selected programming exercises.

Thanks to James Brink, Gerald Cahill, David Topham, and W.A. Barrett. John Taylor is the offical corrections manager.

Copyright 2010 Kip Irvine. All rights reserved.

posted @ 2010-11-09 15:03 JonsenElizee 阅读(83) | 评论 (0) | 编辑收藏

Bash Reference

摘要: [Top] [Contents] [Index] [ ? ] Bash Reference ManualThis text is a brief description of the features that are present inthe Bash shell.... 阅读全文

posted @ 2010-11-04 23:06 JonsenElizee 阅读(111) | 评论 (0) | 编辑收藏

Linux sed reference

sed(C)

sed -- invoke the stream editor

Syntax

sed [ -n ] [ script ] [ -f sfile ] [ file ... ]

sed [ -n ] [ -e script ] ... [ -fsfile ] ... [ file ... ]

Description

The sed command copies the named files(standard input default) to the standard output, edited according to a script ofcommands.

sed takes the following options:

-e script: Read the command script; usually quoted to protect it from theshell.
-f sfile: Take the script from the file sfile; these options accumulate. Ifthere is just one -e option and no -f options, the flag -e may be omitted.
-n: Suppress the default output.

A script consists of editingcommands, one per line, of the following form:

[ address [ , address ] ] function [ arguments ]

In normal operation, sed cyclically copies a line of input into apattern space (unless there is something left after a D command), appliesin sequence all commands whose addresses select that pattern space, and at theend of the script copies the pattern space to the standard output (except under-n) and deletes the pattern space.

A semicolon ``;'' can be used as a command delimiter.

Some of the commands use a hold space to save all or part of the patternspace for subsequent retrieval (see the ``Limitations'' section).

An address is either a decimal number that counts input lines cumulativelyacross files, a ``$'' that addresses the last line of input, or a contextaddress, that is, a /regular expression/ as described in regexp(M),modified as follows:

In a context address, the construction \?regular expression?, where ``?'' is any character, is identical to /regular expression/. Note that in the context address \xabc\xdefx, the second x stands for itself, so that the standard expression is abcxdef.
The escape sequence \n matches a newline embedded in the pattern space.
A dot (.) matches any character except the terminal newline of the pattern space.
A command line with no addresses selects every pattern space.
A command line with one address selects each pattern space that matches the address.
A command line with two addresses separated by a comma selects the inclusive range from the first pattern space that matches the first address through the next pattern space that matches the second. (If the second address is a number less than or equal to the line number first selected, only one line is selected.) Thereafter, the process is repeated, looking again for the first address.

Editing commands can be applied only to nonselectedpattern spaces by use of the negation function ``!'' described in the nextsection.

Functions

In the following list of functions, the maximum number ofpermissible addresses for each function is indicated in parentheses.

The text argument consists of one or more lines, all but the last ofwhich end with backslashes to hide the newlines. Backslashes in text are treatedlike backslashes in the replacement string of an s command, and may beused to protect initial blanks and tabs against the stripping that is done onevery script line.

The rfile or wfile argument must terminate the command line andmust be preceded by one blank. Each wfile is created before processingbegins. There can be at most 10 distinct wfile arguments.

(1) a\ text

Appends text, placing it on the output before reading the nextinput line. Note that there must be a line break between the command and the text.

(2) b label

Branches to the : command bearing the label. If labelis empty, branches to the end of the script.

(2) c\ text

Changes text by deleting the pattern space and then appending text.With 0 or 1 address or at the end of a 2-address range, places text onthe output and starts the next cycle. Note that there must be a line breakbetween the command and the text.

(2) d

Deletes the pattern space and starts the next cycle.

(2) D

Deletes the initial segment of the pattern space through the first newlineand starts the next cycle.

(2) g

Replaces the contents of the pattern space with the contents of the holdspace.

(2) G

Appends the contents of the hold space to the pattern space.

(2) h

Replaces the contents of the hold space with the contents of the patternspace.

(2) H

Appends the contents of the pattern space to the hold space.

(1) i\ text

Insert. Places text on the standard output. Note that there must bea line break between the command and the text.

(2) l

Lists the pattern space on the standard output in an unambiguous way.Nonprinting characters are displayed as a three digit octal number preceded bya backslash ``\''. The following characters are printed as escape sequences:

 -------------------------------------------
 Character              Output
 -------------------------------------------
 backslash              \\
 alert (bell)           \a
 backspace              \b
 form feed              \f
 carriage return        \r
 horizontal tab         \t
 vertical tab           \v

Any output lines that are longer than the output device width(determined by the environment variable COLUMNS) are folded into multiplelines. New lines, inserted when folding a long line, are escaped by apreceding backslash character. The ends of each line in the pattern space aredenoted by a dollar character ``$''.

(2) n

Copies the pattern space to the standard output. Replaces the patternspace with the next line of input.

(2) N

Appends the next line of input to the pattern space with an embeddednewline. (The current line number changes.)

(2) p

Prints (copies) the pattern space on the standard output.

(2) P

Prints (copies) the initial segment of the pattern space through the firstnewline to the standard output.

(1) q

Quits sed by branching to the end of the script. No new cycle isstarted.

(2) r rfile

Reads the contents of rfile and places them on the output beforereading the next input line.

(2) s /regular expression/replacement/flags

Substitutes the replacement string for instances of the regularexpression in the pattern space. Any character may be used instead of``/''. For a more detailed description, see regexp(M).

Flags is zero or more of:

n: Substitute for just the nth occurrence of the regularexpression. n must be an integer greater than zero.
g: Globally substitutes for all non-overlapping instances of the regularexpression rather than just the first one.
p: Prints the pattern space if a replacement was made.
w wfile: Writes the pattern space to wfile if a replacement was made.

(2) t label

Branches to the colon (:) command bearing label if anysubstitutions have been made since the most recent reading of an input line orexecution of a t command. If label is empty, t branchesto the end of the script.

(2) w wfile

Writes the pattern space to wfile.

(2) x

Exchanges the contents of the pattern and hold spaces.

(2) y /string1/string2/

Replaces all occurrences of characters in string1 with thecorresponding characters in string2. The lengths of string1 and string2 must be equal.

(2) ! function

Applies the function (or group, if function is ``{'') onlyto lines not selected by the address(es).

(0) : label

This command does nothing; it bears a label for b and t commands to branch to. Labels can be at most 8 characters long.

(1) =

Places the current line number on the standard output as a line.

(2) {

Executes the following commands through a matching ``}'' only when thepattern space is selected.

(2) !{

Executes the following commands through a matching ``}'' only when thepattern space is not selected.

(0)

An empty command is ignored.

(0) #

Ignore the remainder of the line if # is followed by any othercharacter than ``n'' (treat the line as a comment); if the character ``n''follows #, suppress the default output (equivalent to the command lineoption -n).

Environment variables

COLUMNS: The width of the standard output device in characters; used by the l command for folding long lines. If this variable is not set or it hasan invalid value, sed uses the default value 72.

Exit values

sed continues to process all file argumentseven if one or more of them produces an open error. If there is an open error, sed will exit with a value of 1 when it has finished processing thefiles. A value of 2 indicates a usage error.

Examples

The following examples assume the use of sh(C)or ksh(C).

A common use of sed is to edit a file from within a shell script. Inthis example, every occurrence of the string ``sysman'' in the fileinfile is replaced by ``System Manager''. A temporary file TMP is used tohold the intermediate result of the edit:

   TMP=/usr/tmp/tmpfile_$$
   sed -e 's/sysman/System Manager/g' < infile > $TMP
   mv $TMP infile

In this example, sed removes all blank lines (including those withjust and characters) from padded_file:

   sed '
   /^$/ d
   /^[]*$/ d
   ´ padded_file

sed can be used to strip all lines from a file which do not containa certain string. In this example, all lines in the file infile whichstart with a hash ``#'' are echoed to the screen:

sed -e '/^#/!d'< infile

If several editing commands must be carried out on a file, but the parametersfor the edit are to be supplied by the user, then use echo to appendcommand lines to a sed script. The following example removes alloccurrences of the strings given as arguments to the script from the fileinfile. The name of the temporary file is held by the variable SCRIPT:

   SCRIPT=/usr/tmp/script_$$


   for name in $*
   do
   	echo "s/${name}//g" >> $SCRIPT
   done
   

   TMPFILE=/usr/tmp/tmpfile_$$
   

   sed -f $SCRIPT < infile > $TMPFILE
   

   mv $TMPFILE infile
   

   rm $SCRIPT

Another use of sed is to process the output from othercommands. Here the ps command is filtered using sed to report thestatus of all processes other than those owned by the super user:

ps-ef | sed -e '/^[]*root/d'

Limitations

Both the hold space and pattern space can hold a maximum of8192 bytes.

Standards conformance

sed is conformant with:

ISO/IEC DIS 9945-2:1992, Information technology - Portable Operating SystemInterface (POSIX) - Part 2: Shell and Utilities (IEEE Std 1003.2-1992);
AT&T SVID Issue 2;
X/Open CAE Specification, Commands and Utilities,Issue 4, 1992.

SCO OpenServer Release 5.0.6 -- 1 August 2000

posted @ 2010-11-04 23:02 JonsenElizee 阅读(126) | 评论 (0) | 编辑收藏

C Lib Guide

The C Library Reference Guide

by Eric Huss
© Copyright 1997 Eric Huss

Release 1

Introduction

1.   Language
     1.1  Characters
          1.1.1     Trigraph Characters
          1.1.2     Escape Sequences
          1.1.3     Comments
     1.2  Identifiers
          1.2.1     Keywords
          1.2.2     Variables
          1.2.3     Enumerated Tags
          1.2.4     Arrays
          1.2.5     Structures and Unions
          1.2.6     Constants
          1.2.7     Strings
          1.2.8     sizeof Keyword
     1.3  Functions
          1.3.1     Definition
          1.3.2     Program Startup
     1.4  References
          1.4.1     Pointers and the Address Operator
          1.4.2     Typecasting
     1.5  Operators
          1.5.1     Postfix
          1.5.2     Unary and Prefix
          1.5.3     Normal
          1.5.4     Boolean
          1.5.5     Assignment
          1.5.6     Precedence
     1.6  Statements
          1.6.1     if
          1.6.2     switch
          1.6.3     while  
          1.6.4     do
          1.6.5     for
          1.6.6     goto
          1.6.7     continue
          1.6.8     break
          1.6.9     return
     1.7  Preprocessing Directives
          1.7.1     #if, #elif, #else, #endif
          1.7.2     #define, #undef, #ifdef, #ifndef
          1.7.3     #include
          1.7.4     #line
          1.7.5     #error
          1.7.6     #pragma
          1.7.7     Predefined Macros
2.   Library
     2.1  assert.h
          2.1.1     assert
     2.2  ctype.h
          2.2.1     is... Functions
          2.2.2     to... Functions
     2.3  errno.h 
          2.3.1     EDOM
          2.3.2     ERANGE
          2.3.3     errno   
     2.4  float.h
          2.4.1     Defined Values
     2.5  limits.h
          2.5.1     Defined Values
     2.6  locale.h
          2.6.1     Variables and Definitions
          2.6.2     setlocale
          2.6.3     localeconv
     2.7  math.h
          2.7.1     Error Conditions
          2.7.2     Trigonometric Functions
               2.7.2.1   acos
               2.7.2.2   asin
               2.7.2.3   atan
               2.7.2.4   atan2
               2.7.2.5   cos
               2.7.2.6   cosh
               2.7.2.7   sin
               2.7.2.8   sinh
               2.7.2.9   tan
               2.7.2.10  tanh
          2.7.3     Exponential, Logarithmic, and Power Functions
               2.7.3.1   exp
               2.7.3.2   frexp
               2.7.3.3   ldexp
               2.7.3.4   log
               2.7.3.5   log10
               2.7.3.6   modf
               2.7.3.7   pow
               2.7.3.8   sqrt
          2.7.4     Other Math Functions
               2.7.4.1   ceil
               2.7.4.2   fabs
               2.7.4.3   floor
               2.7.4.4   fmod
     2.8  setjmp.h
          2.8.1     Variables and Definitions
          2.8.2     setjmp
          2.8.3     longjmp
     2.9  signal.h
          2.9.1     Variables and Definitions
          2.9.2     signal
          2.9.3     raise
     2.10 stdarg.h
          2.10.1    Variables and Definitions
          2.10.2    va_start
          2.10.3    va_arg
          2.10.4    va_end
     2.11 stddef.h
          2.11.1    Variables and Definitions
     2.12 stdio.h
          2.12.1    Variables and Definitions
          2.12.2    Streams and Files
          2.12.3    File Functions
               2.12.3.1  clearerr
               2.12.3.2  fclose
               2.12.3.3  feof
               2.12.3.4  ferror
               2.12.3.5  fflush
               2.12.3.6  fgetpos
               2.12.3.7  fopen
               2.12.3.8  fread
               2.12.3.9  freopen
               2.12.3.10 fseek
               2.12.3.11 fsetpos
               2.12.3.12 ftell
               2.12.3.13 fwrite
               2.12.3.14 remove
               2.12.3.15 rename
               2.12.3.16 rewind
               2.12.3.17 setbuf
               2.12.3.18 setvbuf
               2.12.3.19 tmpfile
               2.12.3.20 tmpnam
          2.12.4    Formatted I/O Functions
               2.12.4.1  ...printf Functions
               2.12.4.2  ...scanf Functions
          2.12.5    Character I/O Functions
               2.12.5.1  fgetc
               2.12.5.2  fgets
               2.12.5.3  fputc
               2.12.5.4  fputs
               2.12.5.5  getc
               2.12.5.6  getchar
               2.12.5.7  gets
               2.12.5.8  putc
               2.12.5.9  putchar
               2.12.5.10 puts
               2.12.5.11 ungetc
          2.12.7    Error Functions
               2.12.7.1  perror
     2.13 stdlib.h
          2.13.1    Variables and Definitions
          2.13.2    String Functions
               2.13.2.1  atof
               2.13.2.2  atoi
               2.13.2.3  atol
               2.13.2.4  strtod
               2.13.2.5  strtol
               2.13.2.6  strtoul
          2.13.3    Memory Functions
               2.13.3.1  calloc
               2.13.3.2  free
               2.13.3.3  malloc
               2.13.3.4  realloc
          2.13.4    Environment Functions
               2.13.4.1  abort
               2.13.4.2  atexit
               2.13.4.3  exit
               2.13.4.4  getenv
               2.13.4.5  system
          2.13.5    Searching and Sorting Functions
               2.13.5.1  bsearch
               2.13.5.2  qsort
          2.13.6    Math Functions  
               2.13.6.1  abs
               2.13.6.2  div
               2.13.6.3  labs
               2.13.6.4  ldiv
               2.13.6.5  rand
               2.13.6.6  srand
          2.13.7    Multibyte Functions
               2.13.7.1  mblen
               2.13.7.2  mbstowcs
               2.13.7.3  mbtowc
               2.13.7.4  wcstombs
               2.13.7.5  wctomb
     2.14 string.h
          2.14.1    Variables and Definitions
          2.14.2    memchr
          2.14.3    memcmp
          2.14.4    memcpy
          2.14.5    memmove
          2.14.6    memset
          2.14.7    strcat
          2.14.8    strncat
          2.14.9    strchr
          2.14.10   strcmp
          2.14.11   strncmp
          2.14.12   strcoll
          2.14.13   strcpy
          2.14.14   strncpy
          2.14.15   strcspn
          2.14.16   strerror
          2.14.17   strlen
          2.14.18   strpbrk
          2.14.19   strrchr
          2.14.20   strspn
          2.14.21   strstr
          2.14.22   strtok
          2.14.23   strxfrm
     2.15 time.h 
          2.15.1    Variables and Definitions
          2.15.2    asctime
          2.15.3    clock
          2.15.4    ctime
          2.15.5    difftime
          2.15.6    gmtime
          2.15.7    localtime
          2.15.8    mktime
          2.15.9    strftime
          2.15.10   time
Appendix A
	ASCII Chart
Index
	Index

Questions, comments, or error reports? Please send them toEric Huss

posted @ 2010-11-04 22:50 JonsenElizee 阅读(72) | 评论 (0) | 编辑收藏

Greatest Common Factor

#include < stdio.h >
unsigned int greatest_common_factor( unsigned int M, unsigned int N ){
    unsigned int Rem;
     while ( N > 0 ){
        Rem = M % N;
        M = N;
        N = Rem;
    }

     return M;
}

int main()
{
     int temp;
     int a,b;
    scanf( " %d " , & a);
    scanf( " %d " , & b);
    printf( " the greatest common factor of %d and %d is " ,a,b);
    printf( " %d\n " ,greatest_common_factor(a,b));
    getchar();
     return getchar();
}

this is a demo from ischarles.

posted @ 2010-11-04 14:48 JonsenElizee 阅读(28) | 评论 (0) | 编辑收藏

pow(x, n)

long long pow( int x, unsigned int n)
{
   long long p = 1 ;
   while (n > 0 ) {
     if (n & 1 ) p *= x;
    x *= x;
    n >>= 1 ;
  }
   return p;
}

// this is a demo from micheal

posted @ 2010-11-04 14:35 JonsenElizee 阅读(25) | 评论 (0) | 编辑收藏

Pthread Tutorial

摘要: addNavigation() ... 阅读全文

posted @ 2010-11-01 14:20 JonsenElizee 阅读(428) | 评论 (0) | 编辑收藏

How Many Times Is Needed to Pick Out The Bad Ball

There are y ball with a bad one between them.
all the ball are the same look.
now, give you a balance, how many times do you need to pick out the bad one?

My resolution: need Ball(y) times to pick out the bad one.

#include < stdio.h >
#include < math.h >

int Ball( int y)
{
     if (y <= 3 ) return 1 ;
     return 1 + Ball( y / 3 * 3 == y ? y / 3 : y / 3 + 1 );
}
int main()
{
     int i = 0 ;
     for (i = 2 ; i < 200 ; i ++ ) {
        printf( " Ball(%3d)=%d \t " , i, Ball(i));
         if (i % 5 == 0 ) puts( "" );
    }
    puts( "" );
     return 0 ;
}

posted @ 2010-10-29 09:21 JonsenElizee 阅读(1127) | 评论 (0) | 编辑收藏

Find Median(s) in Billion data with Memory 4M

Issue:
内存只能容纳100W个数,
现在有1亿数,混序,
然后求这一亿个数的中位数,
中位数(就是一个有序数组的中间数字,数组长度为偶数就是两个,奇数则只有一个)

/* *************************************************************************** */
/* this program should find out the median(s) in N(logN)/(logB) no matter there
/* is duplicated data or not.
/*
/* with memory limitation: 4MB memory available. in fact, it can work on 1MB.
/* I would like to express the idea with code.
/* here is just the pseudocode with out any optimization for easy understanding.
/*
/* maybe, there is no need to check sum == N/2 or N/2+1, but this will get the
/* median(s) as soon as possible with out more recursive invoking.
/*
/* sorry for any logical problem. please let me know if you found any.
/**************************************************************************** */

int N = 100000000 ; // total data number is N
int B = 1000000 ;   // number of buckets.
int min, max;
scan data from 0 to N - 1 get min and max; // O(N);

// num the data number that is less than min
// min the minimum data in the target data range to find median(s)
// max the maximum data in the target data range to find median(s)
void find_median( int num = 0 , int min, int max)
{
     if (min == max) {
         if (N % 2 ) {
            print medians are min and max;
        }
         else print median is min; // show you the result
         return ; // exit
    }

     // count all the data in O(N)
     int m = max - min > B ? ((max-min)%B ? (max-min)/B + 1 : (max-min)/B) : 1 ;
     int cnt[B] = { 0 }; // count the data read.
     while ( ! EOF) {
         int data = read_data() - min;
        // count data in this range [min, max]
        // data/m will get the position of data to increase the cnt[?] value
         if (data >= min && data <= max) cnt[data / m] ++ ;
    }

     int sum = num, median_1, median_2, i = 0 ;
     while (sum < N / 2 ) sum += cnt[i ++ ];
    i -- ; // median is in the range of [i*m, (i+1)*m-1]

     /* get median(s) when sum is N/2 */
     if (sum == N / 2 ) {
         if (N % 2 ) { // N is even and there are two medians.
            median_1 = (i + 2 ) * m - 1 ;
            median_2 = i * m;
             while ( ! EOF) {
                 int data = read_data() - min;
                 if (data / m == i) {
                    median_2 = (data > median_2 ? data : median_2);
                }
                 if (data / m == i + 1 ) {
                    median_1 = (data < median_1 ? data : median_1);
                }
            }
            pintf medians are median_1 and median_2;
             return ;
        }

        else { // N is an odd number and there is one median.
            median_1 = (i + 2 ) * m - 1 ;
            while ( ! EOF) {
                int data = read_data();
                if (data / m == i + 1 ) median_1 = (data < median_1 ? data : median_1);
            }
          print median is median_1;
          return ;
        }
    }

     /* get median(s) when sum is N/2+1 */
     if (sum == N / 2 + 1 ) {
         if (N % 2 ) { // N is even and there are two medians.
            median_1 = i * m;
            median_2 = i * m;
             while ( ! EOF) {
                 int data = read_data();
                 if (data / m == i) {
                    median_1 = max;
                    median_2 = (data > median_2 ? data : median_2);
                }
            }
            pintf medians are median_1 and median_2;
             return ;
        }

        else {
            median_2 = i * m; // get (N/2+1)th data.
      while ( ! EOF) {
                int data = read_data();
          if (data / m == i) median_2 = (data > median_2 ? data : median_2);
          }
          print median is median_2;
          return ;
        }
    }


     // if sum is not N/2 or (N/2 + 1), recursively to find out the median(s)
    min = (i + 1 ) * m - 1 ;
    max = i * m;
     // get min and max for next processing
     while ( ! EOF)
    {
         int data = read_data() - min;
         if (data / m == i)
        {
            min = (data < min ? data : min);
            max = (data > max ? data : max);
        }
    }
    find_median(sum, min, max);
}

posted @ 2010-10-28 16:39 JonsenElizee 阅读(1219) | 评论 (0) | 编辑收藏

Kth Star

ISSUE: 输入上百万个行星的位置，求距离第K近的两个行星。

Precondition:
     1 . star field simulation graph is planar.
     2 . the coordinate of star is (x, y) that is treated as a point。
     3 . N = 1000000

1 . bucket - sort all points according to x - coordinate. get B buckets.
    this is will completed in O(NlogN).

    struct bucket {
     int num;        // number of points in this bucket.
    point * points; // points in this bucket.
     double x;       // value of x-coordinate.
   }

   bck[B]; // B buckets got.

2 .
    struct distance {
    point p1;
    point p2;
     double d;      // distance between p1 and p2.
   }

   distance kdis[K]; // to record K small distance. and it's a eliminating-tree.
   kdis[ 0 to K - 1 ] = 0 ;

    for (i = [ 0 , B - 2 ]) // O(B)
   {
     // check bck[i] and bck[i+1]
     if (bck[i + 1 ].x - bck[i].x >= kdis[K - 1 ].d && kdis[K - 1 ] != 0 )
    {
         // there is no need to check these two buckets.
        i ++ ;
         continue ; // save time.
    }

    point * poi = bck[i].points;
     for (j = [ 0 , bck.num - 1 ]) // O(N/B)
    {
        point p = poi[j];
         /*
        find K points in bck[i+1] near to p
        with binary searching method
        according to p.y.
         */
        kp[K]; // K points got in bck[i+1]

         for (m = [ 0 , K - 1 ]) // O(K)
        {
            distance tmp = get_distance(kp[m], p);
             if (tmp.d < kdis[K - 1 ].d)
            {
                kdis[K - 1 ] = tmp;
                 // adjust kdis[K-1], for it's a eliminating tree.
            }
        }
    }
   }

    // finally, the kdis[K-1] is the kth distance in this star graph.
    // the whole processing will be completed in O(NlogN) + O(B*N/B*K).
    // and SC is O(N) + O(K) = O(N).

HOW TO FIND K POINTS ?
     /*
    find K points in bck[i+1] near to p
    with binary searching method
    according to p.y.
     */
it ' s not complecated! and could be found in O(log(N/B)).

posted @ 2010-10-27 15:18 JonsenElizee 阅读(974) | 评论 (0) | 编辑收藏

Get number of 1 from 1 to n

Here is a simple implementation for this issue. And it's TC is O(n/10), O(n);
Any better one is expected.

1 int onenumber( int n)
2 {
3      if (n <= 0 ) return 0 ;
4      if (n <= 9 ) return 1 ;
5
6      int bak = n, hig = 1 , num = 0 ;
7      while (n >= 10 ) {
8         hig *= 10 ;
9         n /= 10 ;
10     }
11
12      if (n == 1 ) {
13         num = bak - hig + 1 + ((bak - hig == 0 ) ? 0 : (bak - hig <= 9 ? 1 : onenumber(bak - hig)));
14         num += (hig - 1 <= 9 ? 1 : onenumber(hig - 1 ));
15     }
16      else {
17         num = (bak - n * hig == 0 ? 0 : (bak - n * hig <= 9 ? 1 : onenumber(bak - n * hig)));
18         num += (n * hig - 1 <= 9 ? 1 : onenumber(n * hig - 1 ));
19     }
20
21      return num;
22 }

posted @ 2010-10-24 19:04 JonsenElizee 阅读(1100) | 评论 (0) | 编辑收藏

Find kth in O(n) TC


 Refer Find kth number in O(n) TC
 
 #include <stdio.h>
 #include  <stdlib.h>
 #include  <time.h>
 
 #define N 20
 
 void init_a(int A[])
 {
   int i = 0;
   for(;i<N;i++)
     A[i]  = rand()%100; 
 }
 
 void print_array(int A[])
 {
    int i = 0;
    for(;i<N;i++)
     {
      if(i==9)
       printf("%d\n",A[i]);
      else
       printf("%d\t",A[i]);
     } 
 }
 
 void swap(int* a, int* b)
 {
    int tmp = *a;
    *a =  *b;
    *b = tmp; 
 }
 
 int rand_partition(int A[], int start,  int end)
 {
    int i = start-1;
    int j = start;
    int num = rand()%(end-start+1)+start;
    swap(A+num,A+end);
    int x = A[end];
    
    for(;j<end;j++)
     {
       if(A[j]<=x)
        {
           i++;
          swap(A+i,A+j); 
         } 
      }
    swap(A+i+1,A+end);
 
    return i+1;
 }
 
 
 int random_select(int A[], int start,  int end, int k)
 {
   int i = 0; 
   if(start  == end)
     return A[start];
     
   int q = rand_partition(A, start, end);
    i = q-start+1;
   
   if(i  == k)
     return A[q];
   else if(i<k)
     return random_select( A, q+1, end, k-i);
   else
     return random_select( A, start, q-1, k); 
 } 
 
 void quick_sort(int A[], int start,  int end)
 {
   if(start<end) 
    {
      int q = rand_partition(A, start, end);
   
       quick_sort( A, q+1, end);
       quick_sort( A, start, q-1);
   } 
 } 
    
 int main(int argc, char *argv[])
 {
   int A[N];
   int num = 0;
   int res = 0;
   srand((unsigned)time(NULL));
    init_a(A);
    print_array(A);
   
    num = rand()%(N-10)+5;
   printf("we begin select %d minimun number\n",num);
    res = random_select( A, 0 , N-1, num); 
   printf("and num is %d\n",res);
   
    quick_sort( A, 0 , N-1);
   printf("after quick sort the array is:\n");
    print_array(A);
   system("PAUSE");    
   return 0;
 }

posted @ 2010-10-24 01:17 JonsenElizee| 编辑收藏

It's Not 1575

there is a car near to a desert with width of 563Km.
and there is a gas station at the left border of the desert.
the car could take 315L gas at most one time.
it can store the gas in the desert for a longer trip.
now, how much gas it need at least to go through the desert?
from the internet, I got a answer 1575. but it's not 1575 in my analysis.

posted @ 2010-10-22 16:46 JonsenElizee| 编辑收藏

Debugging Programs with Multiple Threads

Debugging Programs with Multiple Threads

In some operating systems, such as HP-UX and Solaris, a single program may have more
than one thread of execution. The precise semantics of threads differ from one operating
system to another, but in general the threads of a single program are akin to multiple
processes—except that they share one address space (that is, they can all examine and
modify the same variables). On the other hand, each thread has its own registers and
execution stack, and perhaps private memory.
gdb provides these facilities for debugging multi-thread programs:
• automatic notification of new threads
• ‘thread threadno’, a command to switch among threads
• ‘info threads’, a command to inquire about existing threads
• ‘thread apply [threadno] [all] args’, a command to apply a command to a list of
threads
• thread-specific breakpoints
• ‘set print thread-events’, which controls printing of messages on thread start and
exit.
• ‘set libthread-db-search-path path’, which lets the user specify which libthread_
db to use if the default choice isn’t compatible with the program.
Warning: These facilities are not yet available on every gdb configuration
where the operating system supports threads. If your gdb does not support
threads, these commands have no effect. For example, a system without thread
support shows no output from ‘info threads’, and always rejects the thread
command, like this:
(gdb) info threads
(gdb) thread 1
Thread ID 1 not known. Use the "info threads" command to
see the IDs of currently known threads.
The gdb thread debugging facility allows you to observe all threads while your program
runs—but whenever gdb takes control, one thread in particular is always the focus of
debugging. This thread is called the current thread. Debugging commands show program
information from the perspective of the current thread.
like ‘process 368’, with no further qualifier.
For debugging purposes, gdb associates its own thread number—always a single
integer—with each thread in your program.
info threads
Display a summary of all threads currently in your program. gdb displays for
each thread (in this order):
1. the thread number assigned by gdb
2. the target system’s thread identifier (systag)
3. the current stack frame summary for that thread
An asterisk ‘*’ to the left of the gdb thread number indicates the current thread.
For example,
(gdb) info threads
3 process 35 thread 27 0x34e5 in sigpause ()
2 process 35 thread 23 0x34e5 in sigpause ()
* 1 process 35 thread 13 main (argc=1, argv=0x7ffffff8)
at threadtest.c:68
On HP-UX systems:
For debugging purposes, gdb associates its own thread number—a small integer assigned
in thread-creation order—with each thread in your program.
Whenever gdb detects a new thread in your program, it displays both gdb’s thread
number and the target system’s identification for the thread with a message in the form
‘[New systag]’. systag is a thread identifier whose form varies depending on the particular
system. For example, on HP-UX, you see
[New thread 2 (system thread 26594)]
when gdb notices a new thread.
info threads
Display a summary of all threads currently in your program. gdb displays for
each thread (in this order):
1. the thread number assigned by gdb
2. the target system’s thread identifier (systag)
3. the current stack frame summary for that thread
An asterisk ‘*’ to the left of the gdb thread number indicates the current thread.
For example,
(gdb) info threads
* 3 system thread 26607 worker (wptr=0x7b09c318 "@") \
at quicksort.c:137
2 system thread 26606 0x7b0030d8 in __ksleep () \
from /usr/lib/libc.2
1 system thread 27905 0x7b003498 in _brk () \
from /usr/lib/libc.2
On Solaris, you can display more information about user threads with a Solaris-specific
command:
maint info sol-threads
Display info on Solaris user threads.
thread threadno
Make thread number threadno the current thread. The command argument
threadno is the internal gdb thread number, as shown in the first field of the
‘info threads’ display. gdb responds by displaying the system identifier of the
thread you selected, and its current stack frame summary:
(gdb) thread 2
[Switching to process 35 thread 23]
0x34e5 in sigpause ()
As with the ‘[New ...]’ message, the form of the text after ‘Switching to’
depends on your system’s conventions for identifying threads.
The debugger convenience variable ‘$_thread’ contains the number of the current
thread. You may find this useful in writing breakpoint conditional expressions,
command scripts, and so forth. See See hundefinedi [Convenience
Variables], page hundefinedi, for general information on convenience variables.
thread apply [threadno] [all] command
The thread apply command allows you to apply the named command to one
or more threads. Specify the numbers of the threads that you want affected
with the command argument threadno. It can be a single thread number, one
of the numbers shown in the first field of the ‘info threads’ display; or it could
be a range of thread numbers, as in 2-4. To apply a command to all threads,
type thread apply all command.
set print thread-events
set print thread-events on
set print thread-events off
The set print thread-events command allows you to enable or disable printing
of messages when gdb notices that new threads have started or that threads
have exited. By default, these messages will be printed if detection of these
events is supported by the target. Note that these messages cannot be disabled
on all targets.
show print thread-events
Show whether messages will be printed when gdb detects that threads have
started and exited.
See hundefinedi [Stopping and Starting Multi-thread Programs], page hundefinedi, for
more information about how gdb behaves when you stop and start programs with multiple
threads.
See hundefinedi [Setting Watchpoints], page hundefinedi, for information about watchpoints
in programs with multiple threads.
set libthread-db-search-path [path]
If this variable is set, path is a colon-separated list of directories gdb will use
to search for libthread_db. If you omit path, ‘libthread-db-search-path’
will be reset to an empty list.
On gnu/Linux and Solaris systems, gdb uses a “helper” libthread_db library
to obtain information about threads in the inferior process. gdb will
use ‘libthread-db-search-path’ to find libthread_db. If that fails, gdb will
continue with default system shared library directories, and finally the directory
from which libpthread was loaded in the inferior process.
For any libthread_db library gdb finds in above directories, gdb attempts
to initialize it with the current inferior process. If this initialization fails
(which could happen because of a version mismatch between libthread_db
and libpthread), gdb will unload libthread_db, and continue with the next
directory. If none of libthread_db libraries initialize successfully, gdb will
issue a warning and thread debugging will be disabled.
Setting libthread-db-search-path is currently implemented only on some
platforms.
show libthread-db-search-path
Display current libthread db search path.

posted @ 2010-10-22 13:09 JonsenElizee 阅读(209) | 评论 (0) | 编辑收藏

Funny Program

This is a funny programm and I don't why it happens in this way.
No matter what data input that is composed with different numbers, like 123456,
124578, 235689, 789456, 147896, 321478 and so on. through this program, it will
get a same data ever got.

  1 // funny program by JonsenElizee.
  2 //
  3
  4 #include " stdafx.h "
  5 #include < math.h >
  6 #include < assert.h >
  7 /*
  8 * set value in specified position.
  9 * void* ptr pointer of the start point of bit.
10 * int pos position of the bit to be set and pos starts from 0.
11 * int val value to set. val is 0 or 1.
12 */
13 void setbit( void * ptr, int pos, int val)
14 {
15      /* cast to unsigned char* type pointer */
16     unsigned char * uch = (unsigned char * )ptr;
17
18      /* move pointer */
19     uch += pos / 8 ;
20
21      /* set the bit with right value, 0 or 1. */
22     unsigned char tmp = 1 << (pos % 8 );
23      if ( val && (unsigned char )( * uch & tmp) == 0 ) * uch += tmp;
24      else * uch -= tmp;
25 }
26 unsigned char getbit( void * ptr, int pos)
27 {
28      /* cast to unsigned char* type pointer */
29     unsigned char * uch = (unsigned char * )ptr;
30
31      /* move pointer */
32     uch += pos / 8 ;
33
34      /* set the bit with right value, 0 or 1. */
35     unsigned char tmp = 1 << (pos % 8 );
36      return (unsigned char )( * uch & tmp);
37 }
38
39 unsigned revert_unsigned_int(unsigned ipt)
40 {
41     unsigned opt = 0 ;
42     unsigned short i = 0 ;
43      for (opt = ipt; opt != 0 ; opt /= 10 , i ++ );
44      for (opt = 0 ; ipt != 0 ; ipt /= 10 )
45         opt += (ipt - ipt / 10 * 10 ) * ((unsigned)pow( 10 , -- i));
46      return opt;
47 }
48
49 unsigned sort_unsigned_int(unsigned ipt, int ascend)
50 {
51     unsigned opt = 0 ;
52     unsigned i = 0 ;
53
54      /* get length of input data */
55      for (opt = ipt; opt != 0 ; opt /= 10 , i ++ );
56
57     unsigned char * num = (unsigned char * )malloc(i);
58     memset(num, 0 , i);
59     unsigned char * ptr = num;
60     unsigned char * mov = ptr + 1 ;
61     unsigned n = i;
62
63      /* get each number char of input data */
64      for (; ipt != 0 ; ipt /= 10 )
65         num[ -- i] = (unsigned char )(ipt - ipt / 10 * 10 );
66
67      /* sort the number */
68      for (i = 0 ; i < n - 1 ; i ++ ) {
69          if (ascend) {
70              while (mov > num && mov[ 0 ] < mov[ - 1 ]) {
71                 mov[ 0 ] ^= mov[ - 1 ];
72                 mov[ - 1 ] ^= mov[ 0 ];
73                 mov[ 0 ] ^= mov[ - 1 ];
74                 mov -- ;
75             }
76         }
77          else {
78              while (mov > num && mov[ 0 ] > mov[ - 1 ]) {
79                 mov[ 0 ] ^= mov[ - 1 ];
80                 mov[ - 1 ] ^= mov[ 0 ];
81                 mov[ 0 ] ^= mov[ - 1 ];
82                 mov -- ;
83             }
84         }
85         ptr ++ ;
86         mov = ptr + 1 ;
87     }
88
89      /* convert to a unsigned int */
90      for (opt = i = 0 ; i < n; i ++ )
91     {
92         opt += num[i] * ((unsigned)pow( 10 , n - i - 1 ));
93     }
94
95     free(num);
96      return opt;
97 }
98
99 void loop_to_original_data(unsigned ipt)
100 {
101     assert(ipt < 1000000 );
102      char his[ 1000000 ] = { 0 };
103      while ( 1 ) {
104         printf( " %d " , ipt);
105         unsigned a = sort_unsigned_int(ipt, 1 );
106         unsigned b = sort_unsigned_int(ipt, 0 );
107          if (a == b) {
108             printf( " %d\n " , ipt);
109              return ;
110         }
111         unsigned rst =   b - a;
112          if (getbit(his, rst)) {
113             printf( " %d\n " , rst);
114              break ;
115         }
116          else
117             setbit(his, rst, 1 );
118         ipt = rst;
119     }
120 }
121
122 int main()
123 {
124     loop_to_original_data( 123456 );
125     getchar();
126      return 0 ;
127 }
128
129

posted @ 2010-10-22 08:55 JonsenElizee 阅读(1055) | 评论 (0) | 编辑收藏

String to 0x String

Here is a simple implementation to convert string to 0x string.
Better one is expected ......

1 #include < assert.h >
2 /*
3 * convert string to 0x string.
4 *
5 * const char* ipt input string.
6 * char* opt output 0x string.
7 */
8 void str2Xstr( const char * ipt, char * opt)
9 {
10     assert(ipt != NULL && opt != NULL);
11     assert( sizeof ( char ) == 1 );
12
13      /* add prefix 0x into opt */
14      * opt ++ = ' 0 ' ;
15      * opt ++ = ' x ' ;
16
17      char * bak = opt;
18      while ( * ipt != ' \0 ' ) {
19          /* get the char and cast it to int */
20          char cha = * ipt ++ ;
21         unsigned short tmp = cha;
22          /* assert sizeof char is 1 (8bits) */
23         tmp <<= 8 ;
24         tmp >>= 12 ;
25          if (tmp >= 10 ) * opt ++ = tmp - 10 + ' A ' ;
26          else * opt ++ = tmp + ' 0 ' ;
27
28         tmp = cha;
29         tmp <<= 12 ;
30         tmp >>= 12 ;
31          if (tmp >= 10 ) * opt ++ = tmp - 10 + ' A ' ;
32          else * opt ++ = tmp + ' 0 ' ;
33     }
34      /* terminate string */
35      * opt = 0 ;
36 }
37
38 int main()
39 {
40      char opt[ 64 ] = { 0 };
41     str2Xstr( " 2009-09 " , opt);
42     puts(opt); /* 0x323030392D3039 */
43     getchar();
44      return 0 ;
45 }

Using & operation is a better way:

1 /*
2 * convert string to 0x string.
3 *
4 * const char* ipt input string.
5 * char* opt output 0x string.
6 */
7 void str2Xstr( const char * ipt, char * opt)
8 {
9     assert(ipt != NULL && opt != NULL);
10     assert( sizeof ( char ) == 1 );
11
12      /* add prefix 0x into opt */
13      * opt ++ = ' 0 ' ;
14      * opt ++ = ' x ' ;
15
16      char * bak = opt;
17      while ( * ipt != ' \0 ' ) {
18          /* get the char and cast it to int */
19          char cha = * ipt ++ ;
20         unsigned char tmp = cha;
21          /* assert sizeof char is 1 (8bits) */
22         tmp &= ' \xF0 ' ;
23         tmp >>= 4 ;
24          * opt ++ = tmp >= 10 ? tmp - 10 + ' A ' : tmp + ' 0 ' ;
25
26         tmp = cha;
27         tmp &= ' \x0F ' ;
28          * opt ++ = tmp >= 10 ? tmp - 10 + ' A ' : tmp + ' 0 ' ;
29     }
30      /* terminate string and turn back one step */
31      * opt -- = 0 ;
32 }

posted @ 2010-10-21 11:40 JonsenElizee 阅读(41) | 评论 (0) | 编辑收藏

Int to 0x String

Here is simple implementation for converting int value to 0x string with out sprintf and so on.
Any better way is expected ......

1 #include < assert.h >
2 /*
3 * convert int value to 0x string.
4 *
5 * int ipt input int value.
6 * char* opt output string.
7 */
8 void int2Xstr( int ipt, char * opt)
9 {
10     assert(ipt != NULL && opt != NULL);
11
12      /* add prefix "0x" */
13     *opt ++ = ' 0 ' ;
14     *opt ++ = ' x ' ;
15     opt += 7 ;
16
17      /* number of 4bits-unit */
18      int num = sizeof ( int ) * 2 ;
19
20      /* using << and >> to get 4bits value and convert it to 0x char */
21      for ( int i = 0 ; i < num; i ++ )
22     {
23          /* negative value should be converted to unsigned one */
24         unsigned var = ipt < 0 ? (unsigned)( - ipt) : (unsigned)ipt;
25
26          /* >> and << to clear other bits */
27         var >>= 4 * i;
28         var <<= (num - 1 ) * 4 ;
29         var >>= (num - 1 ) * 4 ;
30
31          /* convert to 0x char */
32          if (var >= 10 ) *opt -- = (var - 10 ) + ' A ' ;
33          else *opt -- = var + ' 0 ' ;
34     }
35 }
36 int main()
37 {
38      char opt[ 32 ] = { 0 };
39     int2Xstr( 1234567890 , opt);
40     puts(opt); /* 0x499602D2 */
41     getchar();
42      return 0 ;
43 }

posted @ 2010-10-21 10:24 JonsenElizee 阅读(49) | 评论 (0) | 编辑收藏

Get The Whole Arrangement of String ( PNN )

Get the whole arrangement of a string.
I got no better method to get this kind of sorting sequence.
Here is a simple implementation of printing whole arrangement.
Better one is expected now...

1
2 #include < assert.h >
3 #define N 10 /* do not set a big number for n! */
4
5 /* *
6 * str target string.
7 * oka sorted content.
8 */
9 void pnn( char * str, char * oka)
10 {
11      /* check str */
12     assert(str != NULL && strlen(str) <= N && strlen(str) >= 1 );
13      if (strlen(str) == 1 ) {
14         printf( " %s%c\n " , oka, * str);
15          return ;
16     }
17      /* i to record which char need to be sort now */
18      int i = 0 ;
19      while ( 1 ) {
20          /* define new container for input str to swap char */
21          char ipt[N];
22         memcpy(ipt, str, strlen(str) + 1 );
23          /* define new container for output str to add char */
24          char opt[N];
25         memcpy(opt, oka, strlen(oka) + 1 );
26          /* get position of char to be sort now */
27          char * ptr = ipt + i ++ ;
28          if ( * ptr == ' \0 ' ) break ;
29          /* swap char with the first one in ipt */
30          if (ptr != ipt) {
31              * ptr ^= * ipt;
32              * ipt ^= * ptr;
33              * ptr ^= * ipt;
34         }
35          /* add char into opt as the last one and set '\0' to end the opt */
36         opt[strlen(oka)] = * ipt;
37         opt[strlen(oka) + 1 ] = ' \0 ' ;
38          /* recursively sort next char */
39         pnn(ipt + 1 , opt);
40     }
41 }
42
43 void permutation( char * str)
44 {
45      char aim[N];
46     memcpy(aim, str, strlen(str) + 1 );
47      char oka[ 1 ] = { ' \0 ' };
48     pnn(aim, oka);
49 }
50
51 int main( int argc, _TCHAR * argv[])
52 {
53     permutation( " 1234567 " );
54     getchar();
55      return 0 ;
56 }

posted @ 2010-10-20 16:48 JonsenElizee 阅读(35) | 评论 (0) | 编辑收藏

Four Lines Implementing String to Long

1 int string2long( char * str, long * rtv)
2 {
3      for ( int i = strlen(str), j = * rtv = 0 ; * str >= ' 0 ' && * str <= ' 9 ' ; i -- , str ++ ){
4          * rtv += ( long )(( * str - ' 0 ' ) * (pow( 10 , i - 1 )));
5     }
6      return * str == ' \0 ' ? 1 : 0 ;
7 }

Please pay attention to j = *rtv = 0;
if there is no "j = ", *rtv will be redefined as int *rtv after ", " and address of rtv will be 0xcccccc.
So, inorder to set value of rtv in if sentence, just use a non-usage variable j.

to invoke the function in this way:

long rtv;
if(string2long("321", &rtv)) printf("rtv = %ld\n", rtv);
else puts("failure");

posted @ 2010-10-20 14:29 JonsenElizee 阅读(45) | 评论 (0) | 编辑收藏

Avoiding Dupliated Computing in Fabonaci

How to avoiding duplicated computing of recursive function like this one:
func(n) = func(n-1) + func(n-2) + func(n-3) and func(1) == func(2) == 1 and func(3) == 2.
or function like this: fabonaci:
fabonaci(n) = fabonaci(n-1) + fabonaci(n-2).

1 int fabo( int n, int * ptr)
2 {
3     printf( " fabo(%d)\n " , n);
4      if (n < 3 )
5     {
6          * ptr = 1 ;
7          return 1 ;
8     }
9      else {
10          int tmp;
11          * ptr = fabo(n - 1 , & tmp);
12
13          return * ptr + tmp;
14     }
15 }
16 int fabonaci( int n)
17 {
18      int tmp;
19      return fabo(n, & tmp);
20 }
21
22 int xxx( int n)
23 {
24     printf( " xxx(%d)\n " , n);
25      if (n < 3 ) return 1 ;
26      else return xxx(n - 1 ) + xxx(n - 2 );
27 }
28 int main()
29 {
30      int n = fabonaci( 10 );
31     printf( " n = %d\n " , n);
32
33     n = xxx( 10 );
34     printf( " n = %d\n " , n);
35     getchar();
36      return 0 ;
37 }

1 /* ********************************************************************** */
2 /* func(n) = func(n-1) + func(n-2) + func(n-3)                           */
3 /* func(1) = 1; func(2) = 1; func(3) = 2;                                */
4 /* ********************************************************************** */
5 int funk( int n, int * n_1, int * n_2)
6 {
7     printf( " funk(%d)\n " , n);
8      if (n == 3 ){
9          * n_1 = 1 ;
10          * n_2 = 1 ;
11          return 2 ;
12     }
13      else {
14          int n_1_1, n_1_2;
15          * n_1 = funk(n - 1 , & n_1_1, & n_1_2);
16          * n_2 = n_1_1;
17          return * n_1 + * n_2 + n_1_2;
18     }
19 }
20 int func( int n)
21 {
22      int n_1, n_2;
23      return funk(n, & n_1, & n_2);
24 }
25 int main()
26 {
27      int n = func( 10 );
28     printf( " n = %d\n " , n);
29     getchar();
30      return 0 ;
31 }

posted @ 2010-10-20 11:48 JonsenElizee 阅读(885) | 评论 (0) | 编辑收藏

Postorder for Binary Tree

摘要: Post order accesing the binary tree with a flag to recording what kind of node is accessed.flag == 0 means made left move or accessed a left node.flag == 1 means made right move or accessed a right no... 阅读全文

posted @ 2010-10-16 14:18 JonsenElizee 阅读(166) | 评论 (0) | 编辑收藏

C I/O

int atoi( const char * nptr);
double atof( const char * nptr);
long atol( const char * nptr);

long int strtol( const char *nptr, char **endptr, int base );
unsigned long int strtoul( const char *nptr, char **endptr, int base );
double strtod( const char *nptr, char **endptr);
char *strchr( const char *s, char c); /* find first position of c in s */
int sscanf( const char *, const char *,

); /* read data from string matching format */
int scanf( const char *,

);
int fprintf( FILE *stream, const char *format,

);
int sprintf( char *buffer, const char *format [, argument]

);

FILE I/O FUNCTIONS

/* ********************************************************************** */
/* FILE* FUNCTIONS
/*********************************************************************** */
FILE * fopen( const char * filepath, const char * mode); // mode: "r": read; "w": write, create if not exist; "a": append, create if not exist;

int fread ( void * buf, size_t size, size_t nitems, FILE * stream); // read nitems chars or to the EOF. so it could read multi-lines.
int fwrite( void * buf, size_t size, size_t nitems, FILE * stream); // write nitems chars or to the '\0' of buf.

char * fgets( char * buf, int nitems, FILE * stream);                 // read at most one line with '\n'(holds it) or terminated by EOF.
int    fputs( char * buf, FILE * stream);                             // write strlen(buf) chars into stream and return real written char number.

int getc(FILE * stream);          // read next char and return EOF on end of file or error.
int putc( int c, FILE * stream);   // return c on success, else EOF(-1).

int fgetc(FILE * stream);         // read next char and return EOF on end of file or error.
int fputc( int c, FILE * stream); // return c on success, else EOF(-1).

int fflush(FILE * stream);        // return 0 on success, else EOF(-1).
int feof(FILE * stream);          // return 1 if reach EOF, else 0.
int fclose(FILE * stream);        // return 0 on success, else EOF(-1).

FILE * freopen( char * filename, char * type, FILE * stream); // redirect stream to filename file
int fgetpos(FILE * stream， * fpos_t filepos); // get current file pointer position.
int fscanf(FILE * stream, char * format,[argument]);
int fseek(FILE * stream, long offset, int fromwhere); // SEEK_SET, SEEK_CUR, SEEK_END.

void setbuf(FILE * steam, char * buf);
int setvbuf(FILE * stream, char * buf, int type, unsigned size); // call it just after opening file.
long ftell(FILE * stream); // get current file pointer position.

/* ********************************************************************** */
/* INT FD FUNCTIONS
/*********************************************************************** */
int close( int fd);
int fcntl( int fd , int cmd);                        // #include
int fcntl( int fd, int cmd, long arg);
int fcntl( int fd, int cmd, struct flock * lock );
int ioctl( int fd, int cmd,[ int * argdx, int argcx]); // #include
int read( int fd, void * buf, int nbyte);
int write( int fd, void * buf, int nbyte);
long lseek( int fd, long offset, int fromwhere);     // SEEK_SET, SEEK_CUR, SEEK_END.

/* ********************************************************************** */
/* STDIO FUNCTIONS
/*********************************************************************** */
char * gets( char * buffer ); // from stdio, over at '\n' and EOF and set '\n' to '\0'.
int fgetchar( void );         // from stdio and return EOF when error occurs.
int getch( void );            // #include , no echoing.
int getchar( void );          // #define getchar() fgetc(stdin)
int getche( void );           // echo char from stdio and continue at '\n'.
int putchar( int ch);        // put char into stdout
int puts( char * string );     // put string into stdout.
int scanf( char * format[,argument,]);

/************************************************************************/
/* TEST ON WINDOWS
/************************************************************************/
#include

#include
/************************************************************************/
/* read line_length chars into line from sourcefile
/* return number of chars really read, else -1 for error.
/************************************************************************/
int read_line( char * line, int line_length, FILE* sourcefile)
{
    assert(sizeof(char) == 1);
     int n = 0;
     while (1)
    {
         char c = fgetc(sourcefile);
         if (ferror(sourcefile)) return -1;
         if (c == EOF || line_length-- == 0) break ;
        *line++ = c;
        n++;
    }
     return n;
}

FILE* open_file_demo( const char * filepath, const char * options)
{
    FILE* fp = fopen(filepath, options);
     if (fp == NULL)
    {
        perror("fopen failure!");
    }
     return fp;
}

void write_file_demo()
{
     char * filepath = "D:/xxx.txt";
     char * options = "a";
    FILE* fp = open_file_demo(filepath, options);
    assert(fp != NULL);
     char content[][16] = {"write ", "file ", "demo"};
     int i = 0;
     for (i = 0; i < 3; i++)
    {
         char * str = content[i];
         //int siz = fwrite(str, 1, strlen(str), fp);
        //if(ferror(fp)) perror("fwrite failure!");

         /* write strlen(str) chars into fp. */
         int rtv = fputs(str, fp); /* rtv = 0 means success. */
         if (rtv == EOF) perror("fputs failure!"); /* rtv = EOF(-1) means error. */
    }
    fputs("\n", fp);
     if (ferror(fp)) perror("fputs failure!");

     if (fclose(fp) != 0) perror("fclose failure!");
}

void read_file_demo()
{
     char * filepath = "D:/xxx.txt";
     char * options = "r";
    FILE* fp = open_file_demo(filepath, options);
    assert(fp != NULL);
     while (feof(fp) == 0)
    {
         char line[128] = {0};
         /* make sure sizeof(line)-1 */
         /* fread could read many lines at one time. */
         /* it will read sizeof(line)-1 chars or to the EOF. */
         // int siz = fread(line, 1, sizeof(line)-1, fp);

         /* fgets just read a line or sizeof(line)-1 chars at one time. */
         // char* rtv = fgets(line, sizeof(line)-1, fp);

         int siz = read_line(line, sizeof (line)-1, fp);
         if (ferror(fp))
        {
            perror("fread failure!");
             break ;
        }

        printf("%s", line);
    }

     if (fclose(fp) != 0) perror("fclose failure!");
}

int main()
{
    write_file_demo();
    read_file_demo();
    puts("Exit");
    getchar();
     return 0 ;
}

posted @ 2010-10-15 16:34 JonsenElizee| 编辑收藏

Pointers

1 int main( int argc, char * argv[])
2 {
3      char * str[] = { " Welcome " , " to " , " Fortemedia " , " Nanjing " };
4      char ** ptr = str + 1 ;
5     printf( " ptr = %s\n " , * ptr);
6     puts( " 1------------------------------ " );
7
8     str[ 0 ] = ( * ptr ++ ) + 2 ; // *ptr 取str+1所指的指针，*ptr + 2 指向了“to”后面的'\0'。
9     printf( " ptr = %s\n " , * ptr);
10     printf( " str = [%s]\n " , str[ 0 ]); // []
11     puts( " 2------------------------------ " );
12
13     str[ 1 ] = * (ptr + 1 );
14     printf( " ptr = %s\n " , * ptr);
15     printf( " str = [%s]\n " , str[ 1 ]); // [Nangjing]
16     puts( " 3------------------------------ " );
17
18     str[ 2 ] = ptr[ 1 ] + 3 ;
19     printf( " ptr = %s\n " , * ptr);
20     printf( " str = [%s]\n " , str[ 2 ]); // [jing]
21     puts( " 4------------------------------ " );
22
23      int x = (str[ 2 ] - str[ 1 ]);printf( " x = %d\n " , x);
24     str[ 3 ] = ptr[ 0 ] + x;
25     printf( " str = [%s]\n " , str[ 3 ]); // [g]
26     printf( " ptr[0] = %s\n " , ptr[ 0 ]);
27     puts( " 5------------------------------ " );
28
29     getchar();
30      return 0 ;
31 }

posted @ 2010-10-15 10:07 JonsenElizee| 编辑收藏

Linux Debug Tool

Categories within Debugging

Bug tracking systems

Projects within Debugging

ald
- The Assembly Language Debugger is a tool for debugging executable programs at the assembly level.
Antiparser
- a fuzz testing and fault injection API.
BASH Debugger
- Patched BASH shell with extra debugging support
Benchmark-Timer
- Times and becnhmarks portions of code
Bug-buddy
- GNOME bug-reporting utility
BugPort
- QA system for software development
BuildBot
- Automates the compile/test cycle of software development
Check
- Unit testing framework for C
checker
- Finds memory errors at runtime
clisp
- ANSI Common Lisp compiler, debugger, and interpreter
CMUCL
- Free implementation of Common Lisp
Condenser
- Findis and removes duplicate Java code
CrocoPat
- Tool for relational querying
Crossroads Load Balancer
- Load balance utility for TCP
CUT
- Unit-testing framework for C, C++, and Objective-C
CxxTest
- JUnit/CppUnit/xUnit-like framework for C++
dbg
- C++ debugging utilities
DBG-Client
- Client for the DBG debugger
DBG-Server
- PHP debugger and profiler
Dbug
- Macro-based debugging library
ddd
- Graphical front end for command line debuggers
dejaGnu
- Framework to test programs
diapergluforth
- Testing tool for shared object libraries
dvbsnoop
- Presents streamed (live) information in human readable form
Dynamic Probes
- Debugger
ELATE
- extensible logging software
Electric Fence
- Memory debugger
f2w helpdesk
- Web-based helpdesk package
GCL
- Compiler and interpreter for Common Lisp
Gdb
- GNU Debugger
ggcov
- GUI for reporting test coverage data
Gnu 8085 Simulator
- A graphical 8085 simulator and assembler with a debugger.
GNU Visual Debugger
- Graphical front end for debuggers
Greg
- Software testing framework
GUSS
- Hardware simulator for debugging
Javachecker
- Performs static analysis for Java source file
jf-unittest
- a C++ unit test framework
Jlint
- Java debugger
kdbg
- GUI for gdb
KMD
- Multi-processor debugger
Kodos
- Tool for working with regular expressions
Ksymoops
- Kernel oops and error message decoder
linice
- Source-level kernel debugger
log4php
- Php port of log4j
memcheck
- Memory debugging tool
MemCheck Deluxe
- Memory usage tracker and leak finder
Memwatch
- Memory leak and corruption detection tool
mpatrol
- Diagnoses run-time errors
Nemiver
- a standalone graphical debugger for the GNOME desktop.
OTRS
- Ticket request and email management system
Perl Critic
- Critiques Perl source code for best-practices
PMD
- Java source code analyzer
Pngcheck
- PNG integrity tester and dumper/debugger
Pounder
- Tests Java GUIs
PuDB
- A full-screen, console-based Python debugger.
pvswitch
- Lets users use different program installations on one machine
PyChecker
- Helps fix bugs in Python source code
PyLint
- Pylint analyzes Python source code
QtUnit
- Testing framework for C++
redet
- Tool for constructing and executing regular expressions
Remote GUD
- Lets you debug a program running on a remote host
RLog
- Message logging facility for C++
rpmlint
- RPM error checker
Scmbug
- Combines any source code version control system with any bug-tracking system
Sedsed
- Generates debug files in sed
Sipsak
- Tests SIP devices and applications
Steel Bank Common Lisp
- Development environment for Common Lisp
Strace
- Debugging tool
Synopsis
- multi-language source code introspection tool
TCLP
- Type checker for Prolog dialects
UDS Collection
- C++ development and debugging library
UPnP-Inspector
- The Inspector is an UPnP Device and Service analyzer.
Valgrind
- Memory debugger
Winpdb
- Python debugger
xpvm
- Graphical console and monitor for PVM
Z80-ASM
- Compiler for the Z80 CPU assembler

posted @ 2010-10-13 23:45 JonsenElizee 阅读(243) | 评论 (0) | 编辑收藏

Get duplicated data number in 0.25 billion data

Get the data number that is not a duplicated one in 0.25 billion data set. the data in this big data set is of type int. And the limitation is that
you can only use 600M memory at most. the time complexity should be O(n).

For the data type is int, so, the range of data is [0, 2^32).
Here is my idea.

/* using two 256M array to record the existing state is the best way. */
int duplicated( int all[], int size)
{
    bit st1[256M] = { 0 }, st2[256M] = { 0 };
     int cnt = 0 ;
     for (dat : all) // for each data in all-data set
    {
         if (dat < 2 ^ 31 ) {
             if (st1[dat] == 0 ) st1[dat] = 1 ;
             else if (st2[dat] == 0 ) { st2[dat] = 1 ; cnt ++ ; }
        }
    }

    reset st1 and st2;
     for (dat : all) // for each data in all-data set
    {
         if (dat >= 2 ^ 31 ) {
            dat -= 2 ^ 31 ;
             if (st1[dat] == 0 ) st1[dat] = 1 ;
             else if (st2[dat] == 0 ) { st2[dat] = 1 ; cnt ++ ; }
        }
    }
     return cnt;
}

/* the time complexity is not a constant, O(1), it's O(2 * size/2), it means O(n). */
/* space complexity is O(1), a constant size depending on your processing division. */
/* if we need to process one billion data with type int, this algorithm can also */
/* work well. because the precondition: 0 <= all[i] < 2^32. */
/* Whitout real implementation and full test, if any bug, any reply will be */
/* appreciated. */

posted @ 2010-10-11 09:42 JonsenElizee 阅读(1352) | 评论 (0) | 编辑收藏

xxx

JonsenElizee

随笔分类(28)

最新评论

B+ tree

Contents

[edit] Details

[edit] Search

[edit] Insertion

[edit] Characteristics

[edit] Implementation

[edit] History

[edit] See also

[edit] References

[edit] External links

R-tree

Contents

[edit] Variants

[edit] Algorithm

[edit] Search

[edit] Insertion

[edit] Bulk-loading

[edit] See also

[edit] References

[edit] External links

sed(C)

Syntax

Description

Functions

Environment variables

Exit values

Examples

Limitations

See also

Standards conformance

The C Library Reference Guide

Categories within Debugging

Bug tracking systems

Projects within Debugging

ald

Antiparser

BASH Debugger

Benchmark-Timer

Bug-buddy

BugPort

BuildBot

Check

checker

clisp

CMUCL

Condenser

CrocoPat

Crossroads Load Balancer

CUT

CxxTest

dbg

DBG-Client

DBG-Server

Dbug

ddd

dejaGnu

diapergluforth

dvbsnoop

Dynamic Probes

ELATE

Electric Fence

f2w helpdesk

GCL

Gdb

ggcov

Gnu 8085 Simulator

GNU Visual Debugger

Greg

GUSS

Javachecker

jf-unittest

Jlint

kdbg

KMD

Kodos