卷积(Convolution)，反卷积(Transposed Convolution)，上采样(UpSample, Interpolation)

卷积(Convolution)

  卷积在我的另一篇blog中有介绍，这里不重复说明，只给出根据卷积的输入，计算输出尺寸的公式。

  设输入到卷积层的输入的size为$(B,C_{in},i_H,i_W,i_D)$，分别表示Batch size，Input Channel，Input Height，Input Width，Input Depth，卷积层的卷积核尺寸Kernel_size为$(k_H,k_W,k_D)$，填充padding为$(p_H,p_W,p_D)$，步长stride为$(s_H,s_W,s_D)$。则输出的size为$(B,C_{out},o_H,o_W,o_D)$，分别表示Batch size，Output Channel，Output Height，Output Width，Output Depth，则

$$o_H=\lfloor \frac{i_H+2\ast p_H-k_H}{s_H}\rfloor +1$$
$$o_W=\lfloor \frac{i_W+2\ast p_W-k_W}{s_W}\rfloor +1$$
$$o_D=\lfloor \frac{i_D+2\ast p_D-k_D}{s_D}\rfloor +1$$

其中$\lfloor \cdot \rfloor$表示向下取整，可以看出，H、W、D三个维度的计算是相同且独立的，其实这个公式十分好理解，对于H、W、D任何一个维度，输入网格数是$i$，加上了padding之后，网格数变为$i+2p$，那么$i+2p-k$就是减去一个kernel_size后的网格数，这个时候除以stride在向下取整，$\lfloor \frac{i+2\ast p-k}{s}\rfloor$的含义就是卷积核移动的步数，而卷积核移动的步数在加上1(加上分子减去的那个kernel_size)，就是输出的网格数。

  一般来说，kernel_size在H、W、D三个维度的值设定成一样的， padding、stride也同样经常设定成一样的。值得一提的是，因为这个向下取整的存在，让我们的反卷积操作变得较为复杂，因为对于不同的输入，输出可能一样，例如i=12,13,14对于k=3，s=3，p=0，其输出都是4，反卷积就需要特殊的设定，来返回成12,13或14。

---

反卷积(Transposed Convolution)

  在有些应用场景，例如图像分割领域，我们输入图像尺寸(H,W)，经过了池化或者步长不为一的卷积层后，图像尺寸会变小为(H’,W’)，但我们又想让神经网络输出同原来一样的尺寸，就需要反卷积、上采样等操作返回原来的尺寸。

  反卷积(Transposed Convolution，过去可能也叫Deconvolution，这一叫法逐渐被抛弃)，也叫分数步长卷积(fractionally strided convolutions)，在正向卷积中，步长一般是正整数，在反卷积的任务中，我们的目标是增大尺寸，步长就变成了分数，例如$\frac{1}{2}$步长就对应正向卷积的步长2，在正向卷积中，我们很容易知道，步长stride=2，卷积核就平移两个像素位计算一次卷积，但是stride=$\frac{1}{2}$，卷积核如何平移$\frac{1}{2}$个像素位呢？

  很巧妙的，我们可以在原来相邻的两个像素位A,B之间加一位0，这样我们从位A平移到位B就需要平移两次，如果我们平移一次，就是stride=$\frac{1}{2}$了。因此，对于正向卷积步长stride=n，反卷积就在每两个像素位之间加上n-1个0，这样平移一位就是stride=$\frac{1}{n}$了。因此分数步长卷积并不是真的步长是分数，而是通过添加若干0，一次只平移一位的方法达到分数步长的目的。

  为了解释反卷积，我们用一种比较直观的方法，利用连接模式(connectivity pattern)，输入经过正向卷积层后，输出的每一个像素位，蕴含了输入的哪些像素位的信息(也就是由哪些像素位计算得到)，我们认为输出的这个像素位同输入的有计算关系的像素位存在某种连接模式。

One way to understand the logic behind zero padding is to consider the connectivity pattern of the transposed convolution and use it to guide the design of the equivalent convolution.

接下来我们一步一步的看，一步一步的利用连接模式推出反卷积的计算公式。下面各图中，对于正向卷积，绿色图是是输入，蓝色图是输出，对于反卷积，蓝色图是输入，绿色图是输出，一般我们认为正向卷积和反卷积有相同的卷积核尺寸。

padding=0, stride=1

  下图展示了，正向卷积参数$(input=4,kernel\_size=3,stride=1,padding=0)$，对应反卷积参数$(inpu{t}^{\prime }=2,kernel\_siz{e}^{\prime }=kernel\_size,strid{e}^{\prime }=1,paddin{g}^{\prime }=2)$，根据连接模式，正向卷积中，绿色图左上角的像素只和蓝色图左上角的像素位有连接关系，在正向卷积和反卷积有相同卷积核尺寸的前提下，在反卷积过程中，会在外围进行$paddin{g}^{\prime }=kernel\_size-1$的填充，你可以验证，这样填充的反卷积，会严格满足各个像素位的连接关系，例如绿色图第一行第二个像素位，与蓝色图第一行两个像素位有连接关系。

因此对于正向卷积$padding=0，stride=1$情况，反卷积$paddin{g}^{\prime }=kernel\_size-1，strdi{e}^{\prime }=1$，反卷积输出满足(注意第一行是正向卷积计算公式)：

$$\begin{array}{rl}outpu{t}^{\prime }& =inpu{t}^{\prime }+2\ast paddin{g}^{\prime }-kernel\_size+1\\ & =input{s}^{\prime }+kernel\_size-1\end{array}$$

padding = n(n>=1), stride = 1

  下图展示了，正向卷积参数$(input=5,kernel\_size=4,stride=1,padding=2)$，对应反卷积参数$(inpu{t}^{\prime }=6,kernel\_siz{e}^{\prime }=kernel\_size,strid{e}^{\prime }=1,paddin{g}^{\prime }=1)$，根据连接模式，正向卷积中，绿色图左上角的像素位和蓝色图左上角的3*3像素位有连接关系，在正向卷积和反卷积有相同卷积核尺寸的前提下，在反卷积过程中，会在外围进行$paddin{g}^{\prime }=kernel\_size-padding-1$的填充，你可以验证，这样填充的反卷积，会严格满足各个像素位的连接关系，例如绿色图第一行第二个像素位，与蓝色图左上角(3行*4列)像素位有连接关系。

因此对于正向卷积$padding=n(n>=1)，stride=1$情况，反卷积$paddin{g}^{\prime }=kernel\_size-padding-1，strdi{e}^{\prime }=1$，反卷积输出满足(注意第一行是正向卷积计算公式)：

$$\begin{array}{rl}outpu{t}^{\prime }& =inpu{t}^{\prime }+2\ast paddin{g}^{\prime }-kernel\_size+1\\ & =input{s}^{\prime }+kernel\_size-2\ast padding-1\end{array}$$

Half (same) padding

  Half padding是$padding=n,stride=1$卷积的特例，要求卷积核尺寸为奇数$kernel\_size=2\ast n+1$，设定$padding=n$近似为卷积核尺寸的一半，所以叫Half padding，由于在这种设定下，$input\_size=output\_size$，所以又叫same padding，这种padding在实际应用中使用频率极高。

  下图展示了，正向卷积参数$(input=5,kernel\_size=3,stride=1,padding=1)$，对应反卷积参数$(inpu{t}^{\prime }=5,kernel\_siz{e}^{\prime }=kernel\_size,strid{e}^{\prime }=1,paddin{g}^{\prime }=1)$，根据连接模式，正向卷积中，绿色图左上角的像素只和蓝色图左上角的(2*2)像素位有连接关系，在正向卷积和反卷积有相同卷积核尺寸的前提下，在反卷积过程中，会在外围进行$paddin{g}^{\prime }=kernel\_size-padding-1$的填充，你可以验证，这样填充的反卷积，会严格满足各个像素位的连接关系，例如绿色图第一行第二个像素位，与蓝色图左上角(2行*3列)像素位有连接关系。

因此对于正向卷积$kernel\_size=2\ast n+1，padding=n(n>=1)，stride=1$情况，反卷积$paddin{g}^{\prime }=kernel\_size-padding-1，strdi{e}^{\prime }=1$，反卷积输出满足(注意第一行是正向卷积计算公式)：
$$\begin{array}{rl}outpu{t}^{\prime }& =inpu{t}^{\prime }+2\ast paddin{g}^{\prime }-kernel\_size+1\\ & =inpu{t}^{\prime }\end{array}$$

Full padding

  Full padding是$padding=n,stride=1$卷积的特例，要求$padding=kernel\_size-1$近似为卷积核尺寸，到达了padding的极限，所以叫Full padding。

  下图展示了，正向卷积参数$(input=5,kernel\_size=3,stride=1,padding=2)$，对应反卷积参数$(inpu{t}^{\prime }=7,kernel\_siz{e}^{\prime }=kernel\_size,strid{e}^{\prime }=1,paddin{g}^{\prime }=0)$，根据连接模式，正向卷积中，绿色图左上角的像素只和蓝色图左上角(3*3)像素位有连接关系，在正向卷积和反卷积有相同卷积核尺寸的前提下，在反卷积过程中，会在外围进行$paddin{g}^{\prime }=kernel\_size-padding-1$的填充，你可以验证，这样填充的反卷积，会严格满足各个像素位的连接关系，例如绿色图第一行第二个像素位，与蓝色图第一行到第三行以及第二列到第四列的交集的像素位有连接关系。

因此对于正向卷积$padding=n(n>=1)，stride=1$情况，反卷积$paddin{g}^{\prime }=kernel\_size-padding-1，strdi{e}^{\prime }=1$，反卷积输出满足(注意第一行是正向卷积计算公式)：
$$\begin{array}{rl}outpu{t}^{\prime }& =inpu{t}^{\prime }+2\ast paddin{g}^{\prime }-kernel\_size+1\\ & =input{s}^{\prime }-kernel\_size+1\end{array}$$

padding=0, strides=m(m>=2)

  下图展示了，正向卷积参数$(input=5,kernel\_size=3,stride=2,padding=0)$，对应反卷积参数$(inpu{t}^{\prime }=2,kernel\_siz{e}^{\prime }=kernel\_size,strid{e}^{\prime }=1,paddin{g}^{\prime }=2)$，这就需要上面讲的分数步长的膨胀原理了，根据连接模式，正向卷积中，绿色图左上角的像素只和蓝色图左上角的像素有连接关系，在正向卷积和反卷积有相同卷积核尺寸的前提下，在反卷积过程中，会在外围进行$paddin{g}^{\prime }=kernel\_size-1$的填充，你可以验证，这样填充的反卷积，会严格满足各个像素位的连接关系，例如绿色图第一行第二个像素位，与蓝色图左上角的像素位有连接关系，绿色图第一行第三个像素位，与蓝色图第一行的两个像素位有连接关系。

因此对于正向卷积$padding=0，stride=m(m>=2)$情况，反卷积$paddin{g}^{\prime }=kernel\_size-1，strdi{e}^{\prime }=1，dilatio{n}^{\prime }=stride-1$，反卷积输出满足(注意第一行是正向卷积计算公式，只不过加入了膨胀系数)：
$$\begin{array}{rl}outpu{t}^{\prime }& =inpu{t}^{\prime }+dilation\ast (inpu{t}^{\prime }-1)+2\ast paddin{g}^{\prime }-kernel\_size+1\\ & =stride\ast (inpu{t}^{\prime }-1)+kernel\_size\end{array}$$

padding=n(n>=1), strides=m(m>=2)

  下图展示了，正向卷积参数$(input=5,kernel\_size=3,stride=2,padding=1)$，对应反卷积参数$(inpu{t}^{\prime }=3,kernel\_siz{e}^{\prime }=kernel\_size,strid{e}^{\prime }=1,paddin{g}^{\prime }=1)$，这同样需要上面讲的分数步长的膨胀原理，根据连接模式，正向卷积中，绿色图左上角的像素只和蓝色图左上角的像素位有连接关系，在正向卷积和反卷积有相同卷积核尺寸的前提下，在反卷积过程中，会在外围进行$paddin{g}^{\prime }=kernel\_size-padding-1$的填充，你可以验证，这样填充的反卷积，会严格满足各个像素位的连接关系，例如绿色图第一行第二个像素位，与蓝色图第一行前两个像素位有连接关系。

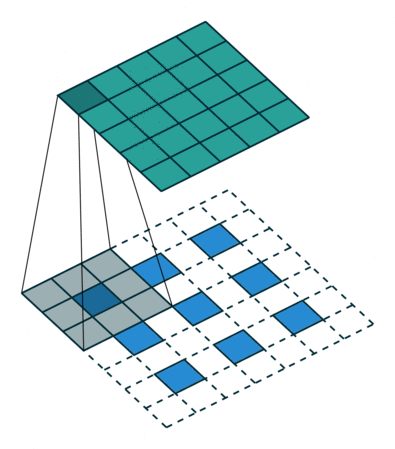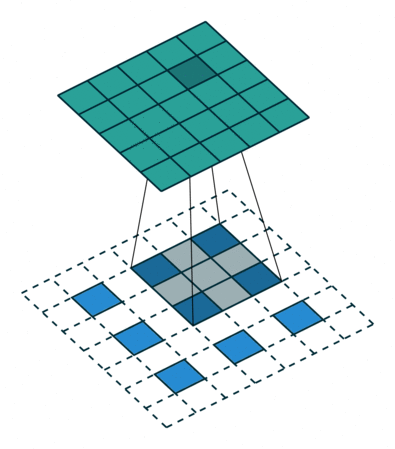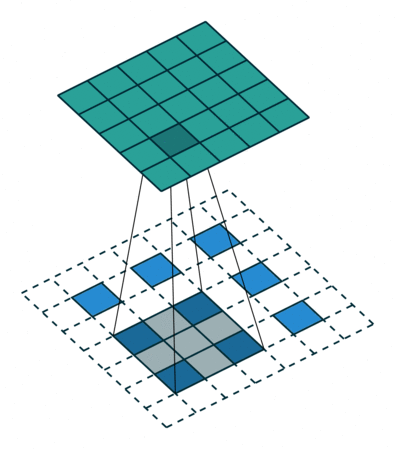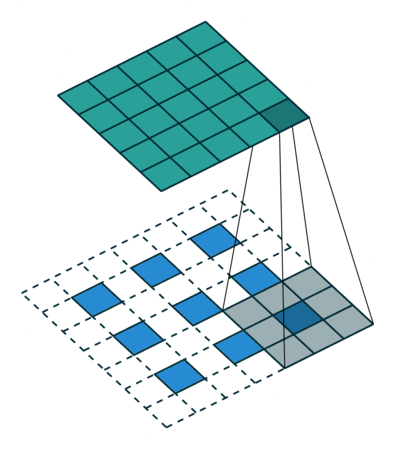
因此对于正向卷积$padding=n(n>=1)，stride=m(m>=2)$情况，反卷积$paddin{g}^{\prime }=kernel\_size-padding-1，strdi{e}^{\prime }=1，dilatio{n}^{\prime }=stride-1$，反卷积输出满足(注意第一行是正向卷积计算公式，只不过加入了膨胀系数)：
$$\begin{array}{rl}outpu{t}^{\prime }& =inpu{t}^{\prime }+dilation\ast (inpu{t}^{\prime }-1)+2\ast paddin{g}^{\prime }-kernel\_size+1\\ & =stride\ast (inpu{t}^{\prime }-1)+kernel\_size-2\ast padding\end{array}$$

最一般形式

  正如我们在分析正向卷积时说的，因为向下取整的关系，同样的输出尺寸可能有不同的输出尺寸，在正向卷积公式中，如果$\frac{i+2\ast p-k}{s}$能够整除，我们可以利用之前讲的反卷积计算公式，此时$i=s\ast N-2\ast p+k$，有没有向下取整都可以。

  如果$i=s\ast N-2\ast p+k+a$，且整数a满足$0<a<s$，由于向下取整的存在，a会被截掉，在反卷积设计中，我们要想办法补上a，我们会在$inpu{t}^{\prime }$的最右边和最上边补上a个zero padding。

a = (i + 2p − k) mod s represents the number of zeros added to the top and right edges of the input

  下图展示了，正向卷积参数$(input=6,kernel\_size=3,stride=2,padding=1)$，对应反卷积参数$(inpu{t}^{\prime }=3,kernel\_siz{e}^{\prime }=kernel\_size,strid{e}^{\prime }=1,paddin{g}^{\prime }=1,a=1)$，根据连接模式，正向卷积中，绿色图左上角的像素只和蓝色图左上角的像素有连接关系，在正向卷积和反卷积有相同卷积核尺寸的前提下，在反卷积过程中，会在外围进行$paddin{g}^{\prime }=kernel\_size-padding-1$的填充，你可以验证，这样填充的反卷积，会严格满足各个像素位的连接关系，例如绿色图第一行第二个像素位，与蓝色图第一行前两个像素位有连接关系，绿色图第一行最后一个像素位，只与蓝色图第一行最后一个像素位有连接关系。

因此对于正向卷积$padding=n(n>=1)，stride=m(m>=2)$情况，反卷积$paddin{g}^{\prime }=kernel\_size-padding-1，strdi{e}^{\prime }=1，dilatio{n}^{\prime }=stride-1，a=(input+2\ast padding-kernel\_size)mods$，反卷积输出满足(注意第一行是正向卷积计算公式，只不过加入了膨胀系数和额外的填充a)：
$$\begin{array}{rl}outpu{t}^{\prime }& =inpu{t}^{\prime }+dilation\ast (inpu{t}^{\prime }-1)+2\ast paddin{g}^{\prime }+a-kernel\_size+1\\ & =stride\ast (inpu{t}^{\prime }-1)+kernel\_size-2\ast padding+a\end{array}$$

---

上采样(UpSample, Interpolation)

  上采样(UpSample)操作其实是一个很大的范畴，反卷积也可以属于上采样操作，但这篇blog的上采样仅仅表示插值(Interpolation)，我们以pytorch的API为例，列举较为常见的双线性插值(bilinear)和最近邻插值(nearest)。

# 双线性插值
inputs = torch.FloatTensor(np.arange(4*4)).reshape(1,1,4,4)
m = nn.Upsample(scale_factor=2, mode='bilinear', align_corners=False)
upsample = m(inputs)

# 待插值输入inputs
tensor([[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]]]])
          
# 双线性插值结果upsample
tensor([[[[ 0.0000,  0.2500,  0.7500,  1.2500,  1.7500,  2.2500,  2.7500, 3.0000],
          [ 1.0000,  1.2500,  1.7500,  2.2500,  2.7500,  3.2500,  3.7500, 4.0000],
          [ 3.0000,  3.2500,  3.7500,  4.2500,  4.7500,  5.2500,  5.7500, 6.0000],
          [ 5.0000,  5.2500,  5.7500,  6.2500,  6.7500,  7.2500,  7.7500, 8.0000],
          [ 7.0000,  7.2500,  7.7500,  8.2500,  8.7500,  9.2500,  9.7500, 10.0000],
          [ 9.0000,  9.2500,  9.7500, 10.2500, 10.7500, 11.2500, 11.7500, 12.0000],
          [11.0000, 11.2500, 11.7500, 12.2500, 12.7500, 13.2500, 13.7500, 14.0000],
          [12.0000, 12.2500, 12.7500, 13.2500, 13.7500, 14.2500, 14.7500, 15.0000]]]])

# 最近邻插值
inputs = torch.FloatTensor(np.arange(4*4)).reshape(1,1,4,4)
m = torch.nn.Upsample(scale_factor=2, mode='nearest')
upsample = m(inputs)

# 待插值输入inputs
tensor([[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]]]])
          
# 最近邻插值结果upsample
tensor([[[[ 0.,  0.,  1.,  1.,  2.,  2.,  3.,  3.],
          [ 0.,  0.,  1.,  1.,  2.,  2.,  3.,  3.],
          [ 4.,  4.,  5.,  5.,  6.,  6.,  7.,  7.],
          [ 4.,  4.,  5.,  5.,  6.,  6.,  7.,  7.],
          [ 8.,  8.,  9.,  9., 10., 10., 11., 11.],
          [ 8.,  8.,  9.,  9., 10., 10., 11., 11.],
          [12., 12., 13., 13., 14., 14., 15., 15.],
          [12., 12., 13., 13., 14., 14., 15., 15.]]]])

  最近邻插值的结果很好理解，双线性插值的结果不太好理解(其实找规律还是可以知道怎么实现的，但不知道为何要这样上采样)，关于双线性插值，我很想看pytorch的源代码，但貌似是C语言写得，不是很懂Cython，找不到代码文件。

---

参考文献：
A guide to convolution arithmetic for deep learning：https://arxiv.org/abs/1603.07285
部分卷积动图的地址：https://github.com/vdumoulin/conv_arithmetic/blob/master/README.md
pytorch：Upsample