Learning‐Based Animation of Clothing for Virtual Try‐On. Santesteban, Igor et al. EG2019
Santesteban, Igor, Miguel A. Otaduy, and Dan Casas. “Learning‐Based Animation of Clothing for Virtual Try‐On.” Computer Graphics Forum. Vol. 38. No. 2. 2019.
1. Motivation
Tight garments follow the deformation of the body.
Inspired by Pose Space Deformation (PSD) and subsequent human body models.
Notification
M b M_b Mb a deformed human body mesh with shape parameters β \beta β and pose parameters θ \theta θ (joint angles).
M c M_c Mc a deformed garment mesh worn by the human body mesh
S c ( β , θ ) S_c(\beta,\theta) Sc(β,θ) the simulated garment result on a body shape with β \beta β and θ \theta θ . This is our goal.
2. Main work
2.1 Cloth model
-
Body deformation model(PSD)
M b ( β , θ ) = W ( T b ( β , θ ) , β , θ , W b ) M_b(\beta,\theta) = W(T_b(\beta,\theta),\beta,\theta,W_b) Mb(β,θ)=W(Tb(β,θ),β,θ,Wb)
in which W ( ⋅ ) W(·) W(⋅) is a skinning function,
T b ( β , θ ) ∈ R 3 × V b T_b(\beta,\theta)\in R^{3×V_b} Tb(β,θ)∈R3×Vb is an unposed body mesh including V b V_b Vb vertices,
T b ( β , θ ) T_b(\beta,\theta) Tb(β,θ) may be obtained by deforming a template body mesh T ‾ b \overline{T}_b Tb to account for body shape and pose-based surface corrections (See, e.g., [LMR∗15]) .
-
Similar cloth deformation pipeline
T ‾ c ∈ R 3 × V c \overline{T}_c\in R^{3×V_c} Tc∈R3×Vc is a template cloth mesh including V c V_c Vc vertices
1.compute an unposed cloth mesh T c ( β , θ ) T_c(\beta,\theta) Tc(β,θ)
T c ( β , θ ) = T ‾ c + R G ( β ) + R L ( β , θ ) T_c(\beta,\theta)=\overline{T}_c +R_G(\beta) + R_L(\beta,\theta) Tc(β,θ)=Tc+RG(β)+RL(β,θ)
R G ( ) R_G() RG() and R L ( ) R_L() RL() represent two nonlinear regressors, which
take as input body shape parameters and shape and pose parameters2.use the skinning function W ( ⋅ ) W(·) W(⋅) to produce the full cloth deformation
M c ( β , θ ) = W ( T c ( β , θ ) , β , θ , W c ) M_c(\beta,\theta) = W(T_c(\beta,\theta),\beta,\theta,W_c) Mc(β,θ)=W(Tc(β,θ),β,θ,Wc)
the skinning weight matrix W c W_c Wc by projecting each vertex of the
template cloth mesh onto the closest triangle of the template body
mesh, and interpolating the body skinning weights W b W_b Wb.3.postprocessing step to get collision-free cloth outputs by pushing them outside
their closest body primitive.
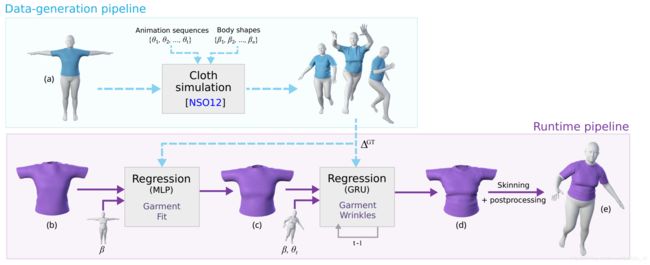
2.2 Garment Fit Regressor (static)
A nonlinear regressor R G : R ∣ β ∣ → R 3 × V c R_G: R^{|\beta|}\rightarrow R^{3×V_c} RG:R∣β∣→R3×Vc
Input: the shape of the body β \beta β
output: per-vertex displacements Δ G \Delta_G ΔG
Ground-truth: Δ G G T = ρ ( S c ( β , 0 ) ) − T ‾ c \Delta^{GT}_G=\rho(S_c(\beta,0))-\overline{T}_c ΔGGT=ρ(Sc(β,0))−Tc
S c ( β , 0 ) S_c(\beta,0) Sc(β,0)represents a simulation of the garment on a body with shape β \beta β and pose θ = 0 \theta=0 θ=0
ρ \rho ρ represents a smoothing operator.
Function: a single-hidden-layer multilayer perceptron (MLP) neural network
Loss: MSE
2.3 Garment Wrinkle Regressor (dynamic)
A nonlinear regressor R L : R ∣ β ∣ + ∣ θ ∣ → R 3 × V c R_L: R^{|\beta|+|\theta|}\rightarrow R^{3×V_c} RL:R∣β∣+∣θ∣→R3×Vc
Input: shape β \beta β and pose θ \theta θ
output: per-vertex displacements Δ L \Delta_L ΔL
Ground-truth: Δ L G T = W − 1 ( S c ( β , θ ) , β , θ , W c ) − T ‾ c − Δ G \Delta^{GT}_L=W^{-1}(S_c(\beta,\theta),\beta,\theta,W_c)-\overline{T}_c- \Delta_G ΔLGT=W−1(Sc(β,θ),β,θ,Wc)−Tc−ΔG
GT represents the deviation between the simulated cloth worn by the moving body, which is expressed in the body’s rest pose.
Function: a Recurrent Neural Network (RNN) based on Gated Recurrent Units (GRU)
Loss: MSE
2.4 Dataset
-
one garment
-
parametric human model(SMPL) including 17 training body shapes: for each of 4 principal components of β \beta β, generate 4 samples + the nominal shape with β = 0 \beta=0 β=0.
-
animation: 56 sequences character motions from the CMU dataset which contain 7117 frames in total(at 30 fps, downsampled from the original CMU dataset of 120 fps). Simulate each of the 56 sequences for each of the 17 body shapes, wearing the same garment mesh( a T-shirt with 8710 triangles).
-
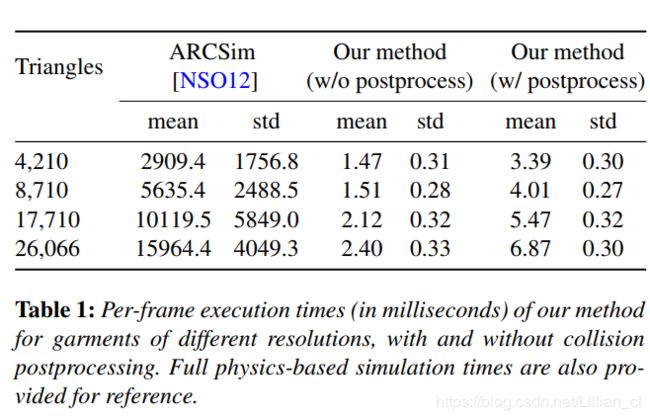
ARCSim:
[parameters]
material: an interlock knit with 60% cotton and 40% polyester
time step: 3.33ms (0.0033s)
store step: 10 time steps
120989 output frames
-
How to get a collision-free initial state for simulation?
1.manually pre-position the garment mesh once on the template
body mesh T ‾ b \overline{T}_b Tb.2.run the simulation to let the cloth relax, and thus define the initial state for all subsequent simulations.
3.apply a smoothing operator ρ ( ⋅ ) \rho(·) ρ(⋅) to this initial state to obtain the
template cloth mesh T ‾ c \overline{T}_c Tc.
-
-
ground-truth garment fit data
interpolate the shape parameters from the template body mesh to the target shape, while simulate the garment from its collision-free initial state. Once the body reaches its target shape, let the cloth rest, and compute the GT garment fit displacements.
-
ground-truth garment wrinkle data
interpolate both shape and pose parameters from the template body mesh to the shape and initial pose of the animation. let the cloth rest.
2.5 Network Implementation and Training
Tensorflow.
MLP for garment fit regression contains a single hidden layer with 20 hidden neurons.
The GRU network for garment wrinkle regression contains a single hidden layer with 1500 hidden neurons.
Dropout regularization. Randomly disable 20% of the hidden neurons
on each optimization step.
Adam for 2000 epochs with an initial learning rate of 0.0001.
Train each network seperatly.
-
The garment fit MLP network
training the ground-truth data from all 17 body shapes.
-
The garment wrinkle GRU network ()
52 animation sequences for training
4 sequences for testing.
batchsize 128.
speed-up: the error gradient using Truncated Backpropagation Through Time
(TBPTT), with a limit of 90 time steps. LSTM中用到。
3. Evaluation
-
Quantitative Evaluation
Linear vs. nonlinear regression

Generalization to new body shapes
Generalization to new body poses: CMU sequences 01_01 and 55_27 -
clothing deformations produced by our approach on a static pose while
changing the body shape over time.
DRAPE approximates the deformation of the garment by scaling it such that it fits the target shape, which produces plausible but unrealistic results. In contrast, our method deforms the garment in a realistic manner.
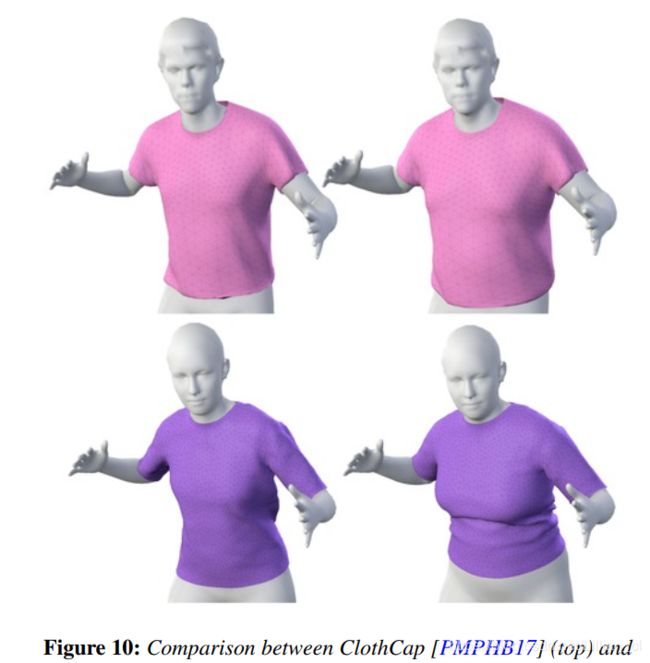
ClothCap’s retargeting lacks realism because cloth deformations are simply copied across different shapes. In contrast, our method produces realistic pose- and shape-dependent deformations.
- Generalization to new poses (01_01)
4. Future work
-
Generalize to multiple garments(with different materials)
-
Collisions(add low-level collision constraints into Network)
-
Smooths excessively high-frequency wrinkles
-
Loose garments (dress).