算法系列笔记5(扩展数据结构-动态顺序统计和区间树)
在编程中,我们往往使用已有的数据结构无法解决问题,这是不必要急着创建新的数据结构,而是在已有数据结构的基础上添加新的字段。本节在上一次笔记红黑树这一基础数据结构上进行扩展,得出两个重要的应用—动态顺序统计和区间树。
动态顺序统计
在算法系列笔记2中我们在线性时间内完成了静态表的顺序统计,而这里我们在红黑树上进行扩展,在O(lgn)时间内完成该操作,主要包括返回第i 排名的元素os_select(i)和给定一个元素x,返回其排名(os_rank(x)).
思想:添加新项:在红黑树的结点上记录下该结点的子树个数。size[x] = size[left[x]] + size[right[x]] +1。 若结点为空,则为0。
此外当你对该扩展的数据结构进行插入和删除操作时,需随时更新子树的大小,与插入和删除操作同步进行,但是需要重新使其回到平衡。主要在于case2和case3这两种情况的旋转。<可以与算法系列笔记4>红黑树的插入代码进行对比,看修改情况。
代码:
返回第i 排名的元素os_select(i)
BSTNode* OSRBTree::os_select(BSTNode *p, const int &ith){
if(p == NULL) return p;
int k = 1;
if(p->left != NULL){
k = p->left->size + 1; // 当前该结点所对应的rank
}
if(ith == k) return p;
if(ith < k) return os_select(p->left, ith);
else return os_select(p->right, ith - k);
}给定一个元素x,返回其排名(os_rank(x))
// return the rank of value
int OSRBTree::os_rank(BSTNode *p, const int &value){
if(p == NULL) return 0;
int k = 1;
if(p->left != NULL)
k = p->left->size + 1;
if(p->val == value)
return k;
else if(p->val > value) return os_rank(p->left, value);
else return os_rank(p->right, value)+k;
}OSTree.h
#ifndef OSRBTREE
#define OSRBTREE
#include
#include
using namespace std;
class BSTNode{
public:
BSTNode *left, *right;
BSTNode *parent;
int val;
string color;
int size;
};
class OSRBTree{
public:
OSRBTree(const int &rootVal){
root = new BSTNode();
root->val = rootVal;
root->left = NULL;
root->right = NULL;
root->color = "black";
root->size = 1;
root->parent = NULL;
}
BSTNode* insertBST(BSTNode *p, const int &value);
void insertOSRBTree(BSTNode *root1, const int &value);
void inorderOSRBTree(BSTNode *p);
BSTNode* os_select(BSTNode *p, const int &ith);
int os_rank(BSTNode *p, const int &value);
public:
BSTNode *root;
};
#endif #include "OSRBTree.h"
// 二叉查找树的插入
BSTNode* OSRBTree::insertBST(BSTNode *p, const int &value){
BSTNode *y = NULL;
BSTNode *in = new BSTNode();
in->left = NULL;
in->right = NULL;
in->val = value;
in->parent = NULL;
in->size = 1;
while(p != NULL){
y = p;
p->size += 1;
if(p->val > in->val)
p = p->left;
else p = p->right;
}
if(y == NULL)
p = in;
else{
in->parent = y;
if(y->val > in->val) y->left = in;
else y->right = in;
}
return in;
}
// 插入红黑树
void OSRBTree::insertOSRBTree(BSTNode *root1, const int &value){
BSTNode * in = insertBST(root1, value);
in->color = "red";
while(in != root1 && in->color == "red"){ // 对红黑特性进行调整
if(in->parent->color == "black") return; // 也就保证了必须
if(in->parent == in->parent->parent->left){
BSTNode *y = in->parent->parent->right;
if(y != NULL && y->color == "red"){ // case 1
y->color = "black";
y->parent->color = "red";
in->parent->color ="black";
in = in->parent->parent;
}
else{
if(in == in->parent->right){ // case 2 in->parent 左旋
BSTNode *pa = in->parent;
in->size = pa->size; // 修改该结点所包含子树结点个数
in->parent = pa->parent;
pa->parent->left = in;
pa->parent = in;
if(pa->left != NULL)
pa->size = pa->left->size + 1; // 修改结点子树结点大小
else pa->size = 1;
if(in->left != NULL){
in->left->parent = pa;
pa->size += in->left->size;
}
pa->right = in->left;
in->left = pa;
in = pa;
}
// case 3 in->parent->parent 右旋
BSTNode *pa = in->parent;
BSTNode *gpa = in->parent->parent;
pa->size = gpa->size;
if(gpa->parent != NULL){
if(gpa == gpa->parent->left){
gpa->parent->left = pa;
}else
gpa->parent->right = pa;
}
pa->parent = gpa->parent;
if(gpa->right != NULL)gpa->size = gpa->right->size + 1;
else gpa->size = 1;
if(pa->right != NULL){
gpa->size += pa->right->size;
pa->right->parent = gpa;
}
gpa->left = pa->right;
pa->right = gpa;
gpa->parent = pa;
pa->color = "black";
gpa->color = "red";
}
}
else{
BSTNode *y = in->parent->parent->left;
if(y != NULL && y->color == "red"){ // case 1
y->color = "black";
y->parent->color = "red";
in->parent->color ="black";
in = in->parent->parent;
}else{ // do the same as A but left与right对换
if(in == in->parent->left){ // case 2 in->parent 右旋
BSTNode *pa = in->parent;
in->size = pa->size; // 修改该结点所包含子树结点个数
in->parent = pa->parent;
pa->parent->right = in;
pa->parent = in;
if(pa->right != NULL)
pa->size = pa->right->size + 1;
else pa->size = 1;
if(in->right != NULL){
in->right->parent = pa;
pa->size += in->right->size;
}
pa->left = in->right;
in->right = pa;
in = pa;
}
// case 3 in->parent->parent 左旋
BSTNode *pa = in->parent;
BSTNode *gpa = in->parent->parent;
pa->size = gpa->size;
if(gpa->parent != NULL){
if(gpa == gpa->parent->left){
gpa->parent->left = pa;
}else
gpa->parent->right = pa;
}
pa->parent = gpa->parent;
if(gpa->left != NULL)gpa->size = gpa->left->size+1;
else gpa->size = 1;
if(pa->left != NULL){
pa->left->parent = gpa;
gpa->size += pa->left->size;
}
gpa->right = pa->left;
pa->left = gpa;
gpa->parent = pa;
pa->color = "black";
gpa->color = "red";
}
}
}
root1->color = "black";
}
// 中序遍历输出
void OSRBTree::inorderOSRBTree(BSTNode *p){
if(p == NULL) return;
if(p->left != NULL) inorderOSRBTree(p->left);
cout << p->val << p->color << p->size << " ";
if(p->right != NULL) inorderOSRBTree(p->right);
}
// give ith smallest value
BSTNode* OSRBTree::os_select(BSTNode *p, const int &ith){
if(p == NULL) return p;
int k = 1;
if(p->left != NULL){
k = p->left->size + 1; // 当前该结点所对应的rank
}
if(ith == k) return p;
if(ith < k) return os_select(p->left, ith);
else return os_select(p->right, ith - k);
}
// return the rank of value
int OSRBTree::os_rank(BSTNode *p, const int &value){
if(p == NULL) return 0;
int k = 1;
if(p->left != NULL)
k = p->left->size + 1;
if(p->val == value)
return k;
else if(p->val > value) return os_rank(p->left, value);
else return os_rank(p->right, value)+k;
}int a[10] = {5,4,6, 7,2,4, 1, 8, 5, 10};
OSRBTree osbrt(a[0]);
for(int i = 1; i < 10; i++)
osbrt.insertOSRBTree(osbrt.root, a[i]);
cout << "中序遍历的结果: " << endl;
osbrt.inorderOSRBTree(osbrt.root);
cout << endl;
int ith = 6;
BSTNode *rank = osbrt.os_select(osbrt.root, ith);
if(rank == NULL) cout << "排名" << ith << "不存在!!" << endl;
cout << "排名" << ith << ": " << rank->val << endl;
int x = 6;
cout << x << "排名为: ";
cout << osbrt.os_rank(osbrt.root, x) << endl;Result:
它们的时间复杂度都为O(lgn),因为红黑树的高度为O(lgn)。
问题:为什么不直接使用这些结点排名作为新添加的项呢?原因在于当你此时对树进行修改时,维护这个树就变得很费劲。
方法论:如
1:选择一个基础的数据结构(red-black tree)
2:在数据统计中维护一些附加信息(子树大小)
3:验证这个数据结构上的信息不会受修改操作的影响(insert, delete---rotations)
4:建立新的运算。假设新的数据已经存好了,然后开始使用这些信息(os_select, os_rank).
区间树(Interval Tree)
问题:保存一系列的区间,比如说时间区间。需要查询集合中的所有区间,与给定区间发生重叠的有哪些?
我们按照上面提到的方法论来进行:
1:选择红黑树作为基本的数据结构,并将区间的较低值(low)作为键值
2:将结点子树的最大值作为新添加的项(m[x] = max{high[int[x]],m[left[x]], m[right[x]]}).
3:是否受插入删除等操作的影响?受,但是在O(1)时间内就能调整过来,见代码。
4:新的操作,查询集合中与给定区间重叠的一个区间。
代码:
IntervalTree.h
#ifndef INTERVALTREE
#define INTERVALTREE
#include
#include
using namespace std;
struct dataNode{
int low;
int high;
};
class BSTNode{
public:
BSTNode *left, *right;
BSTNode *parent;
int val;
dataNode d;
string color;
int m; // 最大值
};
class IntervalTree{
public:
IntervalTree(const dataNode &d)
{
root = new BSTNode();
root->d = d;
root->color = "black";
root->left = NULL;
root->right = NULL;
root->m = d.high;
root->parent = NULL;
root->val = d.low;
}
BSTNode* insertBST(BSTNode *p, const dataNode &d);
void insertIntervalTree(BSTNode *root1, const dataNode &d);
void inorderOSRBTree(BSTNode *p);
BSTNode* intervalSearch(BSTNode *p, const dataNode &d);
public:
BSTNode *root;
void destroyBST(BSTNode *p);
};
#endif
#include "IntervalTree.h"
using namespace std;
BSTNode* IntervalTree::insertBST(BSTNode *p, const dataNode &d){
BSTNode *y = NULL;
BSTNode *in = new BSTNode();
in->left = NULL;
in->right = NULL;
in->val = d.low;
in->parent = NULL;
in->m = d.high;
in->d = d;
while(p != NULL){
y = p;
if(p->m < in->m) p->m = in->m; // 为子树结点的最大值
if(p->val > in->val)
p = p->left;
else p = p->right;
}
if(y == NULL)
p = in;
else{
in->parent = y;
if(y->val > in->val) y->left = in;
else y->right = in;
}
return in;
}
void IntervalTree::insertIntervalTree(BSTNode *root1, const dataNode &d){
BSTNode * in = insertBST(root1, d);
in->color = "red";
while(in != root1 && in->color == "red"){ // 对红黑特性进行调整
if(in->parent->color == "black") return; // 也就保证了必须
if(in->parent == in->parent->parent->left){
BSTNode *y = in->parent->parent->right;
if(y != NULL && y->color == "red"){ // case 1
y->color = "black";
y->parent->color = "red";
in->parent->color ="black";
in = in->parent->parent;
}
else{
if(in == in->parent->right){ // case 2 in->parent 左旋
BSTNode *pa = in->parent;
in->m = pa->m; // 修改该结点所包含子树结点个数
in->parent = pa->parent;
pa->parent->left = in;
pa->parent = in;
if(pa->left != NULL)
pa->m = pa->left->m > pa->m ? pa->left->m : pa->m;
if(in->left != NULL){
in->left->parent = pa;
pa->m = in->left->m > pa->m ? pa->left->m : pa->m;
}
pa->right = in->left;
in->left = pa;
in = pa;
}
// case 3 in->parent->parent 右旋
BSTNode *pa = in->parent;
BSTNode *gpa = in->parent->parent;
pa->m = gpa->m;
if(gpa->parent != NULL){
if(gpa == gpa->parent->left){
gpa->parent->left = pa;
}else
gpa->parent->right = pa;
}
pa->parent = gpa->parent;
if(gpa->right != NULL)gpa->m = gpa->right->m > gpa->m ? gpa->right->m : gpa->m;
if(pa->right != NULL){
gpa->m = pa->right->m > gpa->m ? pa->right->m : gpa->m;
pa->right->parent = gpa;
}
gpa->left = pa->right;
pa->right = gpa;
gpa->parent = pa;
pa->color = "black";
gpa->color = "red";
}
}
else{
BSTNode *y = in->parent->parent->left;
if(y != NULL && y->color == "red"){ // case 1
y->color = "black";
y->parent->color = "red";
in->parent->color ="black";
in = in->parent->parent;
}else{ // do the same as A but left与right对换
if(in == in->parent->left){ // case 2 in->parent 右旋
BSTNode *pa = in->parent;
in->m = pa->m; // 修改该结点所包含子树结点个数
in->parent = pa->parent;
pa->parent->right = in;
pa->parent = in;
if(pa->right != NULL)
pa->m = pa->right->m > pa->m ? pa->right->m : pa->m;
if(in->right != NULL){
in->right->parent = pa;
pa->m = in->right->m > pa->m ? in->right->m : pa->m;
}
pa->left = in->right;
in->right = pa;
in = pa;
}
// case 3 in->parent->parent 左旋
BSTNode *pa = in->parent;
BSTNode *gpa = in->parent->parent;
pa->m = gpa->m;
if(gpa->parent != NULL){
if(gpa == gpa->parent->left){
gpa->parent->left = pa;
}else
gpa->parent->right = pa;
}
pa->parent = gpa->parent;
if(gpa->left != NULL)gpa->m = gpa->left->m > gpa->m ? gpa->left->m : gpa->m;
if(pa->left != NULL){
pa->left->parent = gpa;
gpa->m = pa->left->m > gpa->m ? pa->left->m : gpa->m;
}
gpa->right = pa->left;
pa->left = gpa;
gpa->parent = pa;
pa->color = "black";
gpa->color = "red";
}
}
}
root1->color = "black";
}
void IntervalTree::inorderOSRBTree(BSTNode *p){
if(p == NULL) return;
if(p->left != NULL) inorderOSRBTree(p->left);
cout << p->val << p->color << p->m << " ";
//cout << p->d.low << p->color << p->d.high << " ";
if(p->right != NULL) inorderOSRBTree(p->right);
}
BSTNode* IntervalTree::intervalSearch(BSTNode *p, const dataNode &d){
while(p != NULL && (d.low > p->d.high || d.high < p->d.low)){
if(p->left != NULL && d.low < p->m)
p = p->left;
else p = p->right;
}
return p;
}
void IntervalTree::destroyBST(BSTNode *p){
if(p == NULL) return;
if(p->left != NULL){
destroyBST(p->left);
}
if(p->right != NULL){
destroyBST(p->right);
}
delete p;
}int a[6] = {17, 5, 21, 4, 15, 7};
int b[6] = {19, 11, 23, 8, 18, 10};
vector data;
for(int i = 0; i < 6; i++)
{
dataNode d;
d.low = a[i];
d.high = b[i];
data.push_back(d);
}
IntervalTree interval(data[0]);
for(int i = 1; i < data.size(); i++){
interval.insertIntervalTree(interval.root, data[i]);
}
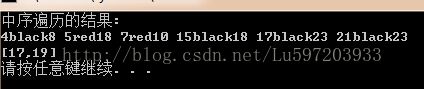
cout << "中序遍历的结果: " << endl;
interval.inorderOSRBTree(interval.root);
cout << endl;
dataNode sd;
sd.low = 18;
sd.high = 25;
BSTNode * bst = interval.intervalSearch(interval.root, sd);
cout << "[" << bst->d.low << "," << bst->d.high << "]" << endl; Result:
时间复杂度都为O(lgn),因为红黑树的高度为O(lgn)。