probability of survival:单位时间段开始时存活的个体,到该时段结束时仍然存活的可能性。
生存率
survival rate:0时刻存活的个体,经历$t_k$个单位时间段后仍然存活的概率。
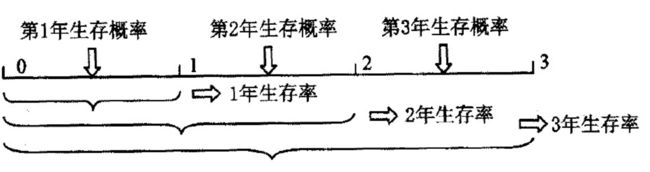
可以看到生存概率表征单位时间内的生存情况,而生存率表征一段时间内的生存情况,生存率又称为累计生存概率。
生存函数
生存率是随时间的变化而变化,它是关于时间的函数,称为生存函数。
生存函数的计算
如果没有删失数据:
$$\hat{S}(t_k)=P(T\geqslant t_k)=\frac{t_k时刻仍存活人数}{总人数}$$
如果有删失数据,需要分段计算生存概率,再将每段的生存概率相乘:
$$\hat{S}(t_k)=P(t\geqslant t_k)=p_1\cdot p_2\cdot \cdots \cdot p_k=\hat{S}(t_{k-1})\cdot p_k$$
中位生存期
median survival time:又称半数生存期,50%的个体存活的时长,即生存率为50%时的时间。
风险函数
hazard function:t时刻存活的个体在t时刻的瞬时死亡率,即在$t$到$t+\Delta t$这一时间段死亡的概率。
$$h(t)=\lim_{\Delta t\rightarrow 0}\frac{P(t
COX模型
表达式
$$h(t)=h_0(t)\cdot e^{\sum_{i=1}^{m}\beta_iX_i}=h_0(t)\cdot e^{\beta_1X_1+\cdots +\beta_mX_m}$$
风险比
hazard ratio:两个群体的风险函数之比。
$$HR=\frac{h_i(t)}{h_j(t)}=\frac{h_0(t)\cdot e^{\beta_{i1}X_{i1}+\cdots +\beta_{im}X_{im}}}{h_0(t)\cdot e^{\beta_{j1}X_{j1}+\cdots +\beta_{jm}X_{jm}}}=e^{\beta_{i1}(X_{i1}-X_{j1})+\cdots +\beta_{im}(X_{im}-X_{jm})}$$
$$lnHR=\beta_{i1}(X_{i1}-X_{j1})+\cdots +\beta_{im}(X_{im}-X_{jm})$$