机器学习面试必知:学生t分布的神奇之处
Gamma分布
G a m ( λ ∣ a , b ) = 1 Γ ( a ) b a λ a − 1 e x p ( − b λ ) Gam(\lambda |a,b)=\frac{1}{\Gamma (a)}b^{a}\lambda ^{a-1}exp(-b\lambda) Gam(λ∣a,b)=Γ(a)1baλa−1exp(−bλ)
高斯分布的精度的共轭先验是Gamma分布。如果我们有一个一元高斯分布 N ( x ∣ u , τ − 1 ) N(x|u,\tau^{-1}) N(x∣u,τ−1)和一个Gamma先验分布 G a m ( τ ∣ a , b ) Gam(\tau|a,b) Gam(τ∣a,b),我们把精度积分出来,我们可以得到x的边缘分布 p ( x ∣ u , a , b ) = ∫ 0 ∞ N ( x ∣ u , τ − 1 ) G a m ( τ ∣ a , b ) d τ p(x|u,a,b)=\int _{0}^{\infty}N(x|u,\tau^{-1})Gam(\tau|a,b)d\tau p(x∣u,a,b)=∫0∞N(x∣u,τ−1)Gam(τ∣a,b)dτ我们定义新的参数 v = 2 a v=2a v=2a和 λ = a b \lambda=\frac{a}{b} λ=ba, p ( x ∣ u , a , b ) p(x|u,a,b) p(x∣u,a,b)变成 S t ( x ∣ u , v , λ ) = Γ ( v + 1 2 ) Γ ( v 2 ) ( λ π v ) 1 2 [ 1 + λ ( x − u ) 2 v ] − v + 1 2 St(x|u,v,\lambda)=\frac{\Gamma(\frac{v+1}{2})}{\Gamma(\frac{v}{2})}(\frac{\lambda}{\pi v})^{\frac{1}{2}}[1+\frac{\lambda (x-u)^{2}}{v}]^{-\frac{v+1}{2}} St(x∣u,v,λ)=Γ(2v)Γ(2v+1)(πvλ)21[1+vλ(x−u)2]−2v+1这就是学生t分布。参数 λ \lambda λ有时被称为t分布的精度,即使它不等于方差的倒数。参数 v v v被称为自由度。当 v = 1 v=1 v=1时,即是柯西分布;当趋向于无穷大时就变成了高斯分布 N ( x ∣ u , λ − 1 ) N(x|u,\lambda^{-1}) N(x∣u,λ−1)。从积分式子中可以看出,学生t分布可以这样通过将无限多个同均值不同精度的高斯分布相加的方式得到。我们可以用matlab来验证:
x=-4:0.01:4; y1=tpdf(x,1)这样生成了一个t分布,运用matlab自带的曲线拟合工具去拟合
我们发现只要3个高斯分布相加就能得到一个拟合度很好的曲线。
我们可以看到学生t分布相比于高斯分布来说通常有着比高斯分布更长的拖尾。
x=-4:0.01:4; y1=tpdf(x,1); y4=pdf('Normal',x,0,1) plot(x,y1,'r-',x,y4,'b-')红线是学生t分布(自由度为1,所以是柯西分布),蓝线是高斯分布(自由度为无穷大的学生t分布)。
更长的拖尾这就赋予了学生t分布一个重要的性质: 鲁棒性。下图对比了高斯分布和t分布(可以用EM算法求得)的最大似然解。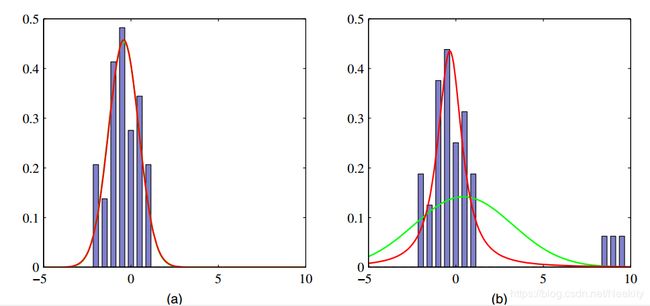
可以看到少量的离群点对于t分布的影响要远远小于高斯分布。这很好地解释了为什么回归的最小平方方法并不具有鲁棒性,因为它对应于高斯分布下的最大似然解。而让回归模型基于一个长拖尾的概率分布例如t分布,我们可以得到一个更具有鲁棒性的模型。