[Note] 关系数据理论
[Note] 关系数据理论
文章目录
- [Note] 关系数据理论
- 目标和问题的提出
- 数据依赖
- 关系模式的简化描述
- 关系的规范化
- 函数依赖(*)
- 定义
- 平凡依赖
- 完全依赖/部分依赖
- 传递依赖
- :horse:
- 范式
- 规范化
- 1NF
- 2NF
- 3NF
- BCNF(3.5NF)
- 多值依赖
- 4NF
- Conclusion
- Conclusion
目标和问题的提出
关系模式是指关系(表)之间的联系.
对于一个现实的场景,应该如何设计关系和关系之间的关系.
比如:冗余项,很多向量的某属性是同一个,这就造成了很大的空间浪费和修改后的完整性校验的隐患.
一个好的关系模式是不会发生异常,以及冗余尽量小.
问题是某些数据依赖造成的.
数据依赖
设U为关系模式中的属性集合.
对于某些属性,确定该(或多个)属性就确定了另一个属性;比如学号和院系.但反过来不行,这就叫函数依赖.记作 f ( n a m e 1 , 2 , . . . . ) = n a m e f(name1,2,....)=name f(name1,2,....)=name.
这样的函数依赖集合记为F.
数据依赖是完整性约束的表现形式,体现于属性值内的关联问题.
- 函数依赖
- 多值依赖
- 连接依赖
关系模式的简化描述
R(U,D,DOM,F)
- R:关系名
- U:属性的集合
- D:U来自的域
- DOM:属性对域的映像集合
- F:属性之间依赖的关系集合
简化为 R < U , F > R
仅保留属性和之间的关系
当r满足F时称r为R的一个关系(实例化)
为优化和排除问题,使用规范化理论进行优化.
关系的规范化
函数依赖(*)
定义
∀ R e l a t i o n s h i p r ∈ U , X , Y ∈ U , i f r ( X ) i s e q u a l , ∄ r ( Y ) i s n o t e q u a l . \forall Relationship\ r\in U,X,Y\in U,if r(X)\ is\ equal,\not\exists r(Y)\ is\ not\ equal. ∀Relationship r∈U,X,Y∈U,ifr(X) is equal,∃r(Y) is not equal.
则称X决定Y或Y依赖X,记作 X → Y X\rightarrow Y X→Y.
注意:X和Y都是U上的属性(组)
否则写作 X ↛ Y X\not\rightarrow Y X→Y
对于该属性的所有下属数据都应该遵守.
反过来说,不能仅仅看关系给出的实例(向量)就推出依赖条件,要研究给出的语义确定.
平凡依赖
X → Y , Y ∉ X X\rightarrow Y,Y\not\in X X→Y,Y∈X
这是非平凡的.
X → Y , Y ∈ X X\rightarrow Y,Y\in X X→Y,Y∈X
这是平凡的.
平凡的函数依赖不反映有意义的语义,所以讨论非平凡的.
完全依赖/部分依赖
如果 X → Y X\rightarrow Y X→Y且 ∀ X ′ ∈ X , X ′ ↛ Y \forall X'\in X,X'\not\rightarrow Y ∀X′∈X,X′→Y,则称Y完全函数依赖X.此时X是最小决定Y的关系集-没有冗余
否则称部分函数依赖.
部分函数依赖意味着有冗余关系属性.
传递依赖
i f X → Y , Y ∉ X , Y ↛ X , Y → Z if\\ X\rightarrow Y,Y\not\in X, Y\not\rightarrow X,Y\rightarrow Z ifX→Y,Y∈X,Y→X,Y→Z
称Z对X传递.
如果 X → Y , Y ∉ X , Y → X X\rightarrow Y,Y\not\in X, Y\rightarrow X X→Y,Y∈X,Y→X,Z为直接依赖.此时X和Y是一对一的关系(函数单调?).
设K为U中的属性组, K → F U K\rightarrow^F U K→FU完全依赖称候选码
如果 K → P U K\rightarrow^P U K→PU部分依赖,称K为超码(?)
候选码是最小的超码
主码
主属性/非主属性
全码
外部码:U中属性(组)X不是R的码但是是另一个关系的码,称X为R的外部码.
See: https://blog.csdn.net/G_beginner/article/details/6773288
Also: https://blog.csdn.net/qq_38213586/article/details/84348470
码
码是一个或多个属性的集合。
超码
是一个或多个属性的集合，超码中的这些属性可以让我们在一个实体集中唯一地标识一个实体。
候选码
候选码是极小的超码集，也就是它的任意真子集都不是超码，而他本身是超码。
主码
主码是被选中用来在一个关系中区分不同元组的候选码。
范式
范式是符合某级别的关系的模式的集合
范式就是对关系模式的不同级别的规范
低级范式包含高级范式
规范化
通过模式分解,将低级关系转化为几个高级关系模式的集合
1NF
所有数据项都是不可分的(即无表中表),所有属性都是同级的不存在附属关系.
最基本的要求
插入异常:当部分主属性合法缺失时无法插入
删除异常:删除部分信息时删除了向量的其他信息
数据冗余大
2NF
每个非主属性都完全函数依赖R的码,不存在部分依赖主属性的属性
也就是属性组R决定而且刚好决定其他每个属性
To reach:分解模式
可以解决1NF的插入和删除问题,简化修改操作.
还是不能完全消除异常和冗余,存在非主属性对码的传递函数依赖
3NF
非主属性没有部分依赖也没有传递依赖.
定义:不存在 X → Y , Y → Z , Y ↛ X X\rightarrow Y,Y\rightarrow Z, Y\not\rightarrow X X→Y,Y→Z,Y→X的X:码;Y:属性组;Z非主属性( Y ∉ Z Y\not\in Z Y∈Z)
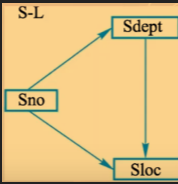
这样的就不是3范式.(Sloc在语义定义中是由Sdept决定的,也就是由Sno决定.下面的箭头是逻辑依赖而不是语义依赖.)
性质:不部分依赖也不传递依赖
BCNF(3.5NF)
所有属性没有部分依赖也没有传递依赖.
进一步消除了主属性对码的函数依赖.
定义:
∀ X → Y a n d X ∉ Y , X 必 含 有 候 选 码 \forall X\rightarrow Y\ and\ X\not\in Y,X必含有候选码 ∀X→Y and X∈Y,X必含有候选码
则称BCNF.
性质:所有非主属性对每一个候选码都是完全函数依赖,所有主属性对每一个不包含的候选码是完全函数依赖,没有任何属性完全函数依赖于非码的任何属性.
BCNF理论上已经达到最大的规范程度.
多值依赖
![[Note] 关系数据理论_第1张图片](http://img.e-com-net.com/image/info8/0b615ea300b54daaa0e33c2d2aea2af6.jpg)
C → → T C\rightarrow\rightarrow T C→→T
有对称性,传递性.
4NF
对于每个非平凡多值依赖 X → → Y X\rightarrow\rightarrow Y X→→Y,X都含有候选码.也就是只允许函数依赖而不允许其他的多值依赖模式
若X->->Y，而Z=U-X-Y空集，则称X->->Y为平凡的多值依赖。否则，称X->->Y为非平凡的多值依赖。
可以看出，如果把上面的一组改为一个，那么多值依赖就变成了函数依赖。当然一个值组成的组也是组，所以说，函数依赖是多值依赖的特殊情况。
Conclusion
范式的作用:消除决定因素非码的非平凡函数依赖
- 1NF消除表中表(非平凡)
- 2NF消除非主属性对码的传递函数依赖
- 3NF消除非主属性对码的传递函数依赖
- BCNF消除主属性对码的部分依赖和传递函数依赖
，称X->->Y为非平凡的多值依赖。
可以看出，如果把上面的一组改为一个，那么多值依赖就变成了函数依赖。当然一个值组成的组也是组，所以说，函数依赖是多值依赖的特殊情况。
Conclusion
范式的作用:消除决定因素非码的非平凡函数依赖
- 1NF消除表中表(非平凡)
- 2NF消除非主属性对码的传递函数依赖
- 3NF消除非主属性对码的传递函数依赖
- BCNF消除主属性对码的部分依赖和传递函数依赖
- 4NF消除非平凡且非函数依赖的多值依赖