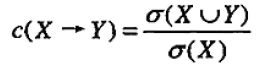机器学习之关联规则(支持度和置信度、Apriori算法)
关联规则及其基础:
关联分析:用于发现隐藏在大型数据集中的有意义的联系。所发现的联系可以用关联规则或频繁项集的形式表示。
例如,从表1中可以提取出:{尿布} ⟹ {啤酒}(该规则表明尿布和啤酒的销售之间存在着很强的联系)。
在对购物篮进行关联分析的时候,需要处理以下两个问题:
1、从大型事务数据集中发现模式可能在计算上要付出很高的代价;
2、所发现的某些模式可能是虚假的,因为它们可能是偶然发生的。
项集(itemset):包含0个或多个项的集合被称为项集;如果一个项集包含k个项,则称它为k项集。空集是指不包含任何项的项集。(例如,{啤酒,尿布,牛奶}是一个3项集)
事务集:全体事务的集合T={t1,t2,…,tn },如2017.11.20日100人超市购物篮记录。其中每一个事务ti都是项的集合且具有一个相关的唯一标识符记为TID,如顾客001购买了{啤酒,尿布,面包}。
频繁项集(Frequent Itemset):项集的相对支持度满足预定义的最小支持度阈值。(一般来说,K项集可能产生 【2的k次方-1】个频繁项集,不包括空集在内)
事务的宽度:事务中出现项的个数。如果项集X是事务 tj 的子集,则称事务 tj 包含项集X。
支持度计数:包含特定项集的事务个数。
关联规则:反映一个事物与其他事物之间的相互依存性和关联性。如果两个或多个事物之间存在一定的关联关系,那么,其中一个事物就能够通过其他事物预测到。
关联规则形如 X ⟹ Y 的蕴涵表达式,其中X和Y是不相交的子集,即(X交Y = 空集)。
关联规则的强度可以用它的支持度和置信度度量。
支持度(suppot):确定规则可以用于给定数据集的频繁程度。
置信度(confidence):确定Y在包含X的事务中出现的频繁程度。
强规则:同时满足最小支持度阈值(minsup)和最小置信度阈值(minconf)的规则称为强规则。
例如,考虑规则{牛奶,尿布} ⟹ {啤酒}。由于项集{牛奶,尿布,啤酒}的支持度计数是2,而事务的总数是5,所以规则的支持度为2/5 = 0.4;规则的置信度是项集{牛奶,尿布,啤酒}的支持度计数与项集{牛奶,尿布}支持度计数的商。由于存在3个事务同时包含牛奶和尿布,所以该规则的置信度为 2/3 = 0.67。
为什么使用支持度和置信度?
支持度是一种重要度量,因为支持度很低的规则可能只是偶然出现。从商务角度来看,低支持度的规则多半也是无意义的,因为对顾客很少同时购买的商品进行促销也是无意义的。因此,支持度通常用来删去哪些无意义的规则。此外,支持度还具有一种期望的性质,可以用于关联规则的有效发现。
置信度通过规则进行推理具有可靠度,对于给定的规则 X ⟹ Y,置信度越高,Y包含在X的事务中出现的可能性就越大。置信度也可以估计Y在给定X下的条件概率。
应当小心解释关联分析的结果。由关联规则作出的推论并不必然蕴涵因果关系。它只表示规则前件和后件中的项明显地同时出现。另一方面,因果关系需要关于数据中原因和结果属性的知识,并且通常涉及长期出现的关系(例如,臭氧损耗导致全球变暖)。
规则剪枝:为了避免进行不必要的计算,事先对规则剪枝,而无需计算它们的支持度和置信度的值将是有益的。(因为规则 X ⟹ Y的支持度仅依赖于其对应项集 X ∪ Y的支持度)。例如,下面的规则具有相同的支持度,因为它们涉及的项都源自同一个项集{啤酒、尿布、牛奶}:
{啤酒、尿布}⟹{牛奶},{啤酒、牛奶}⟹{尿布},
{尿布、牛奶}⟹{啤酒},{啤酒}⟹{尿布、牛奶},
{牛奶}⟹{尿布、啤酒},{尿布}⟹{啤酒、牛奶},
如果项集{啤酒、尿布、牛奶}是非频繁的,则可以立即剪掉这6个候选规则,而不必计算它们的置信度值。
Apriori算法:
第一个关联规则挖掘算法,Agrawal和R.Srikant于1994年提出的,为布尔关联规则挖掘频繁项集的原创性算法。它使用一种称作逐层搜索的迭代算法,通过K项集用于搜索(K+1)项集。已经为大部分商业产品所使用。
步骤如下:
1、首先,通过扫描数据集,产生一个大的候选数据项集,并计算每个候选数据项发生的次数,然后基于预先给定的最小支持度生成频繁1项集的集合,该集合记作L1;
2、然后基于L1和数据集中的数据,产生频繁2项集L2;
3、用同样的方法,直到生成频繁n项集,其中已不再可能生成满足最小支持度的(N+1)项集;
4、最后,从大数据项集中导出规则。
重要的特点:
1、Apriori算法是一个逐层(level-wise)算法,即从频繁1项集到最长的频繁项集,它每次遍历项集格中的一层;
2、Apriori算法使用产生-测试策略来发现频繁项集。在每次迭代之后,新的候选项集都由前一次迭代发现的频繁项集产生,然后对每个候选的支持度进行计数,并于最小支持度阈值进行比较。
Apriori算法支持度先验性质
先验原理:
1、如果一个项集是频繁的,则它的所有子集一定也是频繁的;
2、如果项集是非频繁的,则它的所有超集也一定是非频繁的。
Apriori算法产生候选项集
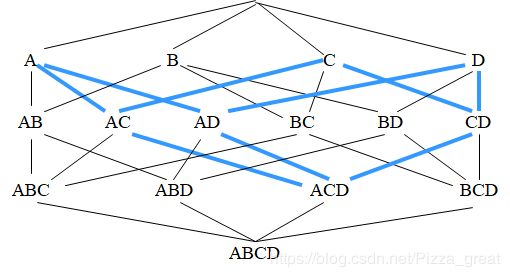
用图2表示上述性质,例子中有四个项目{A,B,C,D},格中的线表示子集关系,频繁项集的性质表明:
如原来的项集是频繁的,则在路径中位于其上的任何集合也一定是频繁的。
如其任意一个子集不是频繁的,则原来的项集也不是频繁的。
Apriori算法置信度
一条规则P➞H的可信度定义为support(P | H)/support(P),其中“|”表示P和H的并集,可信度的计算是基于项集的支持度的。
要找到关联规则,我们首先从一个频繁项集开始。从上面的例子可以得到,如果有频繁项集{A,C},那么就可能有一条关联规则“A➞C”。这意味着如果有人购买了A,那么在统计上他会购买C的概率较大;注意这一条反过来并不总是成立,也就是说,置信度(“A➞C”)并不等于置信度(“C➞A”)。
如果规则X->Y-X不满足置信度阈值,则形如X'->Y-X'的规则也一定不满足置信度阈值,其中X'是X的子集。
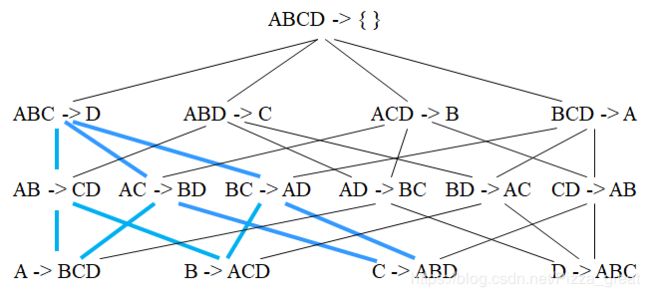
Apriori算法产生关联规则
图3给出了从项集{A,B,C,D}(假设该项集为频繁项集)产生的所有关联规则,其中蓝色线条指向的是低置信度的规则。可以发现如果{ABC}➞{D}是一条低置信度规则,那么所有其他箭头右部包含D的规则均为低置信度的。
极大频繁项集和闭频繁项集
极大频繁项集(Maximal Frequent Itemset):频繁项集X的所有真超项集都不是频繁的。
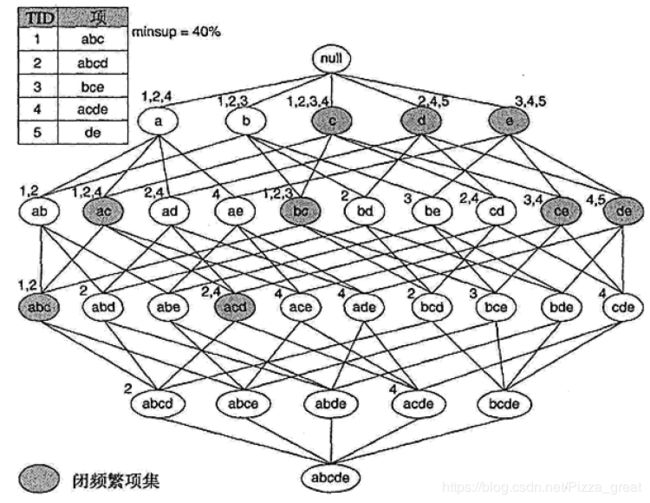
如图4所示,位于边界上方的每个项集都是频繁的,而位于边界下方的项集(阴影结点)都是非频繁的。在边界附近的结点中,{a,d}、{a,c,e}和{b,c,d,e}都是极大频繁项集,因为它们的直接超集都是非频繁的。例如,项集{a,d}是极大频繁的,因为它的所有直接超集{a,b,d}、{a,c,d}和{a,d,e}都是非频繁的;相反,项集{a,c}不是极大的,因为它的一个直接超集{a,c,e}是频繁的。
极大频繁项集有效地提供了频繁项集的紧凑表示;极大频繁项集形成了可以导出所有频繁项集的最小的项集的集合。
闭频繁项集(Closed Frequent Itemset):
闭项集(closed itemset):项集X的真超项集的支持度计数不等于它本身的支持度计数。
Y是X的真超项集:X是Y的子集,但Y中至少有一个项不在X中(真超项集=直接超集=超集=真子集)。
闭频繁项集(Closed Frequent Itemset):X在T中是闭的和频繁的。
换句话说如至少存在一个X的直接超集,其支持度计数与X相同,X就不是闭的。
如图5,格中每个结点(项集)都标出了与它相关联的事务的ID。由于结点{b,c}与事务ID{1,2,3}相关联,因为它的支持度计数为3.从图5中给定的事务可以看出,包含b的每个事务也包含c,因此,由于{b}和{b,c}的支持度是相同的,所以{b}不是闭项集。同样,由于c出现在所有包含a和d的事务中,所以项集{a,d}不是闭的。另一方面,{b,c}是闭项集,因为它的支持度计数与它的任何超集都不同。
假设支持度阈值为40%,则项集{b,c}是闭频繁项集,因为它的支持度是60%。
关联规则挖掘方法分类
基于规则中处理的变量的类别,关联规则可以分为布尔型和数值型。
布尔型关联规则:如果规则考虑的关联是项“在”或“不在”,则关联规则是布尔型的。例如,性别=“女”⟹职业=“秘书”。
量化型关联规则:如果描述的是量化的项或属性之间的关联,则该规则是量化型的关联规则。
例如,性别=“女”⟹avg(月收入)=2300。
基于规则中数据的抽象层次,可以分为单层关联规则和多层关联规则。
单层的关联规则:所有的变量都不涉及不同抽象层次的项或属性。例如,buys(X, “computer”) ⟹buys(X, “printer”),其中X为某顾客。
多层的关联规则:变量涉及不同抽象层次的项或属性。例如:
age(X,“30…39”)⟹buys(X, “laptop computer”)
age(X,“30…39”)⟹buys(X, “computer”)
基于规则中涉及到的数据的维数,关联规则可以分为单维的和多维的。
单维关联规则:处理单个维中属性间的关系,即在单维的关联规则中,只涉及到数据的一个维。
例如,用户购买的物品:“咖啡=>砂糖”,这条规则只涉及到用户的购买的物品。
多维关联规则:处理多个维中属性之间的关系,即在多维的关联规则中,要处理的数据将会涉及多个维。
例如,性别=“女”⟹职业=“秘书”,这条规则就涉及到两个维中字段的信息,是两个维上的一条关联规则。