【PyTorch学习笔记】19：Batch Normalization

归一化(Normalization)

简述

现在常使用ReLU函数，避免梯度弥散的问题，但是有些场合使用Sigmoid这样的函数效果更好（或者是必须使用），如Sigmoid函数当函数值较大或者较小时，其导数都接近0，这会引起梯度弥散，所以要将输入控制在一个较好的范围内，这样才避免了这种问题。

Batch Normalization就是为了解决这个需求的，当将输出送入Sigmoid这样的激活函数之前，进行一个Normalize的操作，例如将其变换到$N(0,{\sigma }^2)$，即在0的附近，主要在一个小范围内变动。

直观解释

左图是输入的$x$范围相差较大的情况，这不仅导致了相应权值$w1$和$w2$的变化引起的变化幅度不同，还会使得搜索空间看起来有点"扭曲"，如果是像右图一样，从哪个位置开始搜索应该都能更好的找到全局最优。

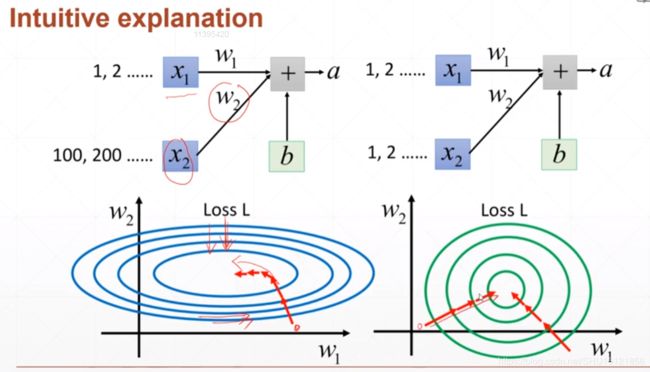
也就是说，这是一个**特征缩放（feature scaling）**的操作。

图像数据是如何做Normalization的

如果是图像数据，例如RGB三个通道的图像数据，其输入的范围是在[0, 1]（如果是[0, 255]就直接除以255就变换到[0, 1]了）。刚刚学了如果数据能符合$N(0,{\sigma }^2)$这样输入进去才是最好的，可以理解成激活函数在0附近的取值对训练最有帮助。例如Sigmoid肯定是使用其0附近的这块，其梯度是最明显的；而ReLU如果只使用正的部分也没有意义了（就和没变换一样）！这里对其进行一个Normalize的操作，也就是各个位置减去均值，然后除以标准差，将其变换到$N(0,1)$上。

各种Normalization方式

[1]标准的Batch Normalization

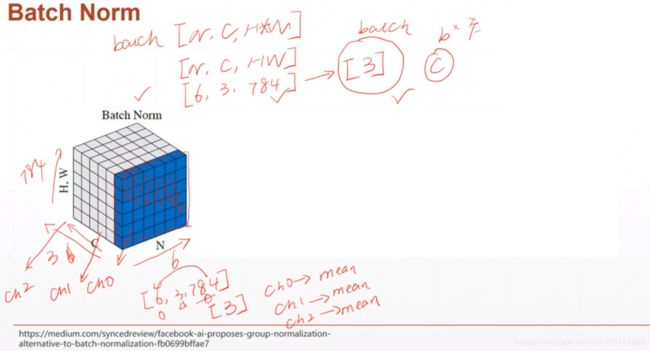
一个Batch的图像数据shape为[样本数N, 通道数C, 高度H, 宽度W]，将其最后两个维度flatten，得到的是[N, C, H*W]，标准的Batch Normalization就是在通道Channel这个维度上进行移动，对所有样本的所有值求均值和方差，所以有几个通道，得到的就是几个均值和方差。

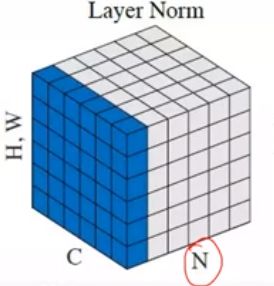
[2]Layer Normalization

Layer Normalization是在实例即样本N的维度上滑动，对每个样本的所有通道的所有值求均值和方差，所以一个Batch有几个样本实例，得到的就是几个均值和方差。

[3]Instance Normalization

Instance Normalization是在样本N和通道C两个维度上滑动，对Batch中的N个样本里的每个样本n，和C个通道里的每个样本c，其组合[n, c]求对应的所有值的均值和方差，所以得到的是$N\cdot C$个均值和方差。

[4]Group Normalization

何恺明提出的归一化方式，老师没讲，见网上资料。

Batch Normalization

简述

这节课只学了传统的Batch Normalization。如下图输入数据是6张3通道784个像素点的数据，将其分到三个通道上，在每个通道上也就是[6, 784]的数据，然后分别得到和通道数一样多的统计数据均值$\mu$和方差$\sigma$，将每个像素值减去$\mu$除以$\sigma$也就变换到了接近$N(0,1)$的分布，后面又使用参数$\beta$和$\gamma$将其变换到接近$N(\beta ,\gamma )$的分布。

注意，$\mu$和$\sigma$只是样本中的统计数据，是没有梯度信息的，不过会保存在运行时参数里。而$\gamma$和$\beta$属于要训练的参数，他们是有梯度信息的。

PyTorch中的使用

如果要查看网络中一个层上的所有参数，用vars(layer)查看。

1d

import torch
from torch import nn

# 随机生成一个Batch的模拟,100张16通道784像素点的数据
# 均匀分布U(0~1)
x = torch.rand(100, 16, 784)

# Batch Normalization层,因为输入是将高度H和宽度W合成了一个维度,所以这里用1d
layer = nn.BatchNorm1d(16)  # 传入通道数
out = layer(x)

# 全局的均值mu
print(layer.running_mean)
# 全局的方差sigma^2
print(layer.running_var)

运行结果：

tensor([0.0500, 0.0498, 0.0499, 0.0501, 0.0500, 0.0502, 0.0500, 0.0500, 0.0500,
        0.0500, 0.0499, 0.0501, 0.0500, 0.0499, 0.0499, 0.0502])
tensor([0.9084, 0.9084, 0.9083, 0.9084, 0.9084, 0.9083, 0.9083, 0.9083, 0.9083,
        0.9083, 0.9084, 0.9084, 0.9083, 0.9083, 0.9083, 0.9083])

注意layer.running_mean和layer.running_var得到的是全局的均值和方差，不是当前Batch上的，只不过这里只跑了一个Batch而已所以它就是这个Batch上的。现在还没有办法直接查看某个Batch上的这两个统计量的值。

2d

x = torch.randn(1, 16, 7, 7)  # 1张16通道的7乘7的图像

# Batch Normalization层,因为输入是有高度H和宽度W的,所以这里用2d
layer = nn.BatchNorm2d(16)  # 传入通道数
out = layer(x)

print(out.shape)
print(layer.running_mean)  # 全局的均值mu
print(layer.running_var)  # 全局的方差sigma^2
print(layer.weight)  # weight也就是前面学的公式里的gamma
print(layer.bias)  # bias也就是前面学的公式里的beta

运行结果：

torch.Size([1, 16, 7, 7])
tensor([ 0.0187,  0.0125, -0.0032,  0.0032,  0.0034,  0.0031,  0.0231, -0.0024,
         0.0002,  0.0194, -0.0097,  0.0177,  0.0324, -0.0013,  0.0128, -0.0086])
tensor([0.9825, 0.9799, 0.9984, 0.9895, 0.9992, 0.9809, 0.9919, 0.9769, 0.9928,
        0.9949, 1.0055, 1.0368, 0.9867, 0.9904, 1.0097, 0.9910])
Parameter containing:
tensor([0.5925, 0.5662, 0.1066, 0.0073, 0.9517, 0.0476, 0.0416, 0.2041, 0.8666,
        0.6467, 0.7665, 0.0300, 0.9050, 0.8024, 0.2816, 0.1745],
       requires_grad=True)
Parameter containing:
tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       requires_grad=True)

注意这里的layer.weight和layer.bias是当前batch上的。

如果在定义层时使用了参数affine=False，那么就是固定$\gamma =1$和$\beta =0$不自动学习，这时参数layer.weight和layer.bias将是None。

Train和Test时的行为不同

这点类似于Dropout，Batch Normalization在训练和测试时的行为不同。

注意，在定义layer后，看到参数train=True表示现在在训练模式（默认），train=False表示在测试模式。
要切换为Test模式，需要在定义layer后使用layer.eval()将其转换！而不是直接写参数train=False。因为总要在训练了之后再做测试吧！如果这种参数放到层的定义时去指定，那就没法切换了（因为定义只有一次）。

在训练模式下，如前面所学的会在训练时去计算均值和方差，并且会自动更新$\gamma$和$\beta$（如果没有关闭自动更新）。在测试时一个样本一个样本进来，归一化所使用的均值和方差都是全局的layer.running_mean和layer.running_var，并且因为不需要训练，不涉及$\gamma$和$\beta$的更新。

总结

使用了$\gamma$和$\beta$之后，最后得到的分布是往$N(\beta ,\gamma )$上靠的，而不是往$N(0,1)$上靠的。

使用了Batch Normalization让Converge（收敛）的速度加快了，这个可以直观理解，使用了靠近0的部分的Sigmoid激活，其梯度信息更大了。并且能够得到一个更好的解。

提升了Robust（鲁棒性），这使得网络更加稳定，这可以从最前面第一张图所示来直观理解，如果参数有大有小，解空间像左边一样，那么稍微调整学习率可能就发生抖动（如图中左侧椭圆解空间上下方向走，且学习率太大时）或者训练速度太慢（如图中右侧椭圆解空间左右方向走，且学习率太小时）。这让超参数的调整没有那么敏感。