CS231N-2017课程作业（assignment 1）之KNN

Cs231n-2017课程作业（assignment 1）之KNN

KNN算法理解：（百度百科）

  KNN也即k-Nearest Neighbor,K（最）近邻分类算法，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例（也即是K个邻居，可根据一定的距离计算公式寻找邻居，如曼哈顿距离，欧式距离等）， 这K个实例的多数属于某个类，就把该输入实例分类到这个类中。

更形象的理解如下：图中有两个不同的类，分别是蓝色的正方形所属的一类和红色的三角所属的一类，我们的目的是预测出绿色的圆属于他们中的那一类？  

• 如果K=3，绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类
• 如果K=5，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类

于此我们看到，当无法判定当前待分类点是从属于已知分类中的哪一类时，我们可以依据统计学的理论看它所处的位置特征，衡量它周围邻居的权重，而把它归为(或分配)到权重更大的那一类。这就是K近邻算法的核心思想。

KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。KNN 算法本身简单有效，它是一种 lazy-learning 算法，分类器不需要使用训练集进行训练，训练时间复杂度为0。KNN 分类的计算复杂度和训练集中的文档数目成正比，也就是说，如果训练集中文档总数为 n，那么 KNN 的分类时间复杂度为O(n)。

---

参考：

作业代码下载：https://github.com/Burton2000/CS231n-2017

参考理解博客：https://blog.csdn.net/u014485485/article/details/79433514

环境配置：

Window7 64位 + Jupyter notebook (通过anaconda安装，python3.6)

数据下载：

下载CIFAR-10数据库：http://www.cs.toronto.edu/~kriz/cifar.html，下载CIFAR-10 python version解压到cs231n/datasets目录下。

开始做作业：

点开 knn.ipynb对每一个cell,shift+enter运行。

首先是加载数据

可以看出训练集含有50000张32*32的图片，测试集含有10000张。

可视化数据集，cifar-10中共有10个分类，每一个类随机选取7张图片：

代码内 函数分析：

numpy.flatnonzero(a)：返回非0元素的索引，a可以是一个表达式

x.ravel()[np.flatnonzero(x)]可以使用它来提取非0元素

np.arange(-2, 3) # 从-2 开始，到3结束，不包含3的数组 [-2,-1,0,1,2]

numpy.random.choice(a, size=None, replace=True, p=None)：对一维数组a产生一个随机采样。size指的是输出形状，replace表示放回还是不放回,p可代表a中样本被采样的概率情况，即自定义取样概率。

为了后面减少计算量，随机采样数据集，训练集采样5000张，测试集采样500张，并将32*32*3的图片reshape成一行：
函数解析：

numpy.reshape(a, newshape, order='C')

np.reshape(a, (a.shape[1], a.shape[0]))：转置等同于np.transpose(a)

当数据的形状不确定时，如果想转换为1行，列数不确定的话，newshape可以传入(1, -1);如果想转换为1列，行数不确定的话，newshape可以传入(-1, 1);同理如果是2列或者2行的话，就是(-1, 2)或者(2，-1)。 -1代表不确定

导入k近邻分类器模块：

(A) 利用两层循环计算L2距离：即

其中两层循环是指从原始训练集（50000）中分两次抽取截取的训练集数（5000）进行L2计算。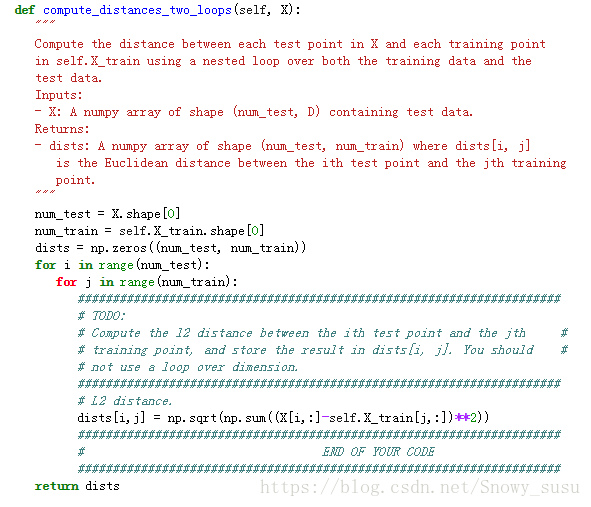

可视化距离矩阵：（本人没看懂是什么意思）

knn不需要训练，直接进行预测，k=1：

Got 137 / 500 correct => accuracy: 0.274000

函数解析：argsort(a, axis=-1, kind='quicksort', order=None)排序，得到前k个近邻的标签，然后得到投票结果

numpy.bincount(x, weights=None, minlength=0)对一维数组x统计各值出现的次数，x里必须是非负整数

numpy.argmax(a, axis=None, out=None)返回最大值

再令k=5预测：

Got 139 / 500 correct => accuracy: 0.278000 精度比k=1时稍高。

结果验证，验证结果为：

(B)在一个loop中完成L2距离计算，并用F范数与两个loop时的结果比较

验证正确性：（用numpy数组运算的特性（broadcast），自动进行维数扩展），其中，F范数代表：

(C)不使用loop计算L2距离就是将距离函数拆开，完成各个单项后再合并

（x - y）^2 = x^2 - 2*x*y + y^2

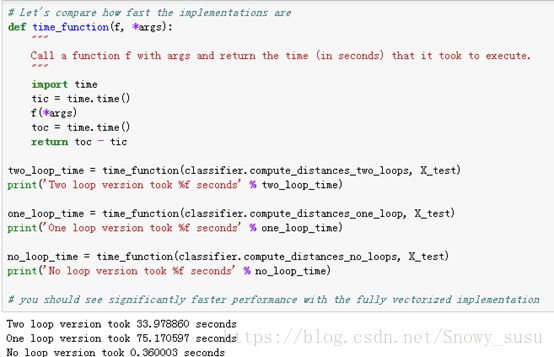
比较三种方法的优劣，高下立现：

交叉验证：

将训练集分成5等分，同时观察不同的k下的分类精度，执行5次kNN算法，将其中一份数据作为验证集，其他作为测试集，取测试集的精度：

取平均精度，画出k-精度图：

可以看出，kNN的分类精度高也就30%，不实用。最佳k咱们取10：

Got 141 / 500 correct => accuracy: 0.282000 度28.2%.

总结：

  KNN 即K-Nearest Neighbor在图像分类中一半不做使用，引起效率低，而且是对像素级的计算，对于图像来说计算量太大，效率慢，且对于对图像做轻微的改变，比如部分像素块遮盖，图像下移，背景渲染等做一小部分的改变可能不会改变L2的值，KNN的检测结果则是相同的图片。通过这个例子可以熟悉图像分类的一般过程，训练，测试；以及对数据集进行交叉验证的方法，很值得学习。