AI应用开发基础傻瓜书系列3-激活函数和损失函数
Copyright © Microsoft Corporation. All rights reserved.
适用于License版权许可
更多微软人工智能学习资源,请见微软人工智能教育与学习共建社区
- Content
- 01.0-神经网络的基本工作原理
- 01.1-基本数学导数公式
- 01.2-Python-Numpy库的点滴
- 02.0-反向传播与梯度下降
- 02.1-线性反向传播
- 02.2-非线性反向传播
- 02.3-梯度下降
- 03.0-损失函数
- 03.1-均方差损失函数
- 03.2-交叉熵损失函数
- 04.0-单入单出单层-单变量线性回归
- 04.1-最小二乘法
- 04.2-梯度下降法
- 04.3-神经网络法
- 04.4-梯度下降的三种形式
- 04.5-实现逻辑非门
- 05.0-多入单出单层-多变量线性回归
- 05.1-正规方程法
- 05.2-神经网络法
- 05.3-样本特征数据的归一化
- 05.4-归一化的后遗症
- 05.5-正确的推理方法
- 05.6-归一化标签值
- 06.0-多入多出单层神经网络-多变量线性分类
- 06.1-二分类原理
- 06.2-线性二分类实现
- 06.3-线性二分类结果可视化
- 06.4-多分类原理
- 06.5-线性多分类实现
- 06.6-线性多分类结果可视化
- 07.0-激活函数
- 07.1-挤压型激活函数
- 07.2-半线性激活函数
- 07.3-用双曲正切函数分类
- 07.4-实现逻辑与门和或门
- 08.0-单入单出双层-万能近似定理
- 08.1-双层拟合网络的原理
- 08.2-双层拟合网络的实现
- 09.0-多入多出双层-双变量非线性分类
- 09.1-实现逻辑异或门
- 09.2-理解二分类的工作原理
- 09.3-非线性多分类
- 09.4-理解多分类的工作原理
- 10.0-调参与优化
- 10.1-权重矩阵初始化
- 10.2-参数调优
- 10.3-搜索最优学习率
- 10.4-梯度下降优化算法
- 10.5-自适应学习率算法
- 11.0-深度学习基础
- 11.1-三层神经网络的实现
- 11.2-验证与测试
- 11.3-梯度检查
- 11.4-手工测试训练效果
- 11.5-搭建深度神经网络框架
- 12.0-卷积神经网络
- 12.1-卷积
- 12.2-池化
- 14.1-神经网络模型概述
- 14.2-Windows模型的部署
- 14.3-Android模型的部署
第三篇:激活函数和损失函数
在这一章,我们将简要介绍一下激活函数和损失函数~
激活函数
看神经网络中的一个神经元,为了简化,假设该神经元接受三个输入,分别为 x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3,那么 z = ∑ i w i x i + b i z=\sum\limits_{i}w_ix_i+b_i z=i∑wixi+bi,
激活函数也就是 A = σ ( Z ) A=\sigma(Z) A=σ(Z)这一步了,他有什么作用呢?
- 从模仿人类大脑的角度来说:
神经元在利用突触传递信息时,不是所有信息都可以传递下去的,每个神经元有自己的阈值,必须要刺激强过某个阈值才会继续向后传递。激活函数在某些方面就可以扮演这样一个激活阈值的作用,不达到一定要求的信号是不可以继续向后传递的
- 说得形象一点,
假设老张家有一个在滴(漏)水的水龙头:水龙头漏水这件事情的严重等级有09这样10个的等级,凭借自己的力量可以解决02这样3的等级的情况,维修部门可以解决36这样的等级,然后譬如需要修改水管线路什么的就是需要更加专业的部门了,他们可以解决79这样等级的情况。发现一个等级为5的漏水事件,处理步骤是什么样的呢?
首先,看到水龙头在滴水,通过视觉细胞处理成信号输入大脑,经过大脑这个黑盒子复杂的处理,判断出这不是简简单单拧紧或者拍拍就能解决的漏水的问题,也就是说,判断出这个事情的严重等级大于2,执行这样一个处理函数:
if 严重等级 > 2:
老张打电话给隔壁老王寻求帮助
else:
自己解决
这件事情的严重等级超过了自己能力的阈值,所以需要开始传递给隔壁老王,之后老王执行一个类似的判断
if 严重等级 > 6:
寻求物业公司帮助
else:
老王拿着管钳去老张家帮忙
类似这个例子中的判断需不需要更专业的人来解决问题,如果严重等级超过了某个设定的阈值,那就需要寻找更专业的人来帮助。在这里的阈值就是能解决的严重等级的上限。
激活函数在神经网络中起到的就是在控制自己接收到的消息到底是不是需要向后传播的作用。
-
从数学的角度来说
形如 z = ∑ i w i x i + b i z=\sum\limits_{i}w_ix_i+b_i z=i∑wixi+bi的传递是一种线性的传递过程。如果没有非线性函数添加非线性,直接把很多层叠加在一起会怎么样呢?
以两层为例:
(1) z 1 = w 1 x 1 + b 1 z_1 = w_1x_1 + b_1 \tag{1} z1=w1x1+b1(1)
(2) z 2 = w 2 z 1 + b 2 = w 2 ( w 1 x 1 + b 1 ) + b 2 = ( w 2 w 1 ) x 1 + ( w 2 b 1 + b 2 ) = w 3 x 1 + b 3 z_2 = w_2z_1 + b_2 = w_2(w_1x_1 + b_1) + b_2 = (w_2 w_1) x_1 + (w_2b_1 + b_2)=w_{3}x_1+b_{3} \tag{2} z2=w2z1+b2=w2(w1x1+b1)+b2=(w2w1)x1+(w2b1+b2)=w3x1+b3(2)
z 1 , z 2 z_1, z_2 z1,z2即为这两个神经元结点的输出。可以看到,叠加后的 z 2 z_2 z2的输出也是一个线性函数。
以此类推,如果缺少非线性层,无论如何叠加,最后得到的还只是一个线性函数。
然而,按照生活经验来说,大多数的事情都不是线性规律变化的,比如身高随着年龄的变化,价格随着市场的变化。所以需要给这样一个线性传递过程添加非线性才可以更好的去模拟这样一个真实的世界。具体该怎么做呢?
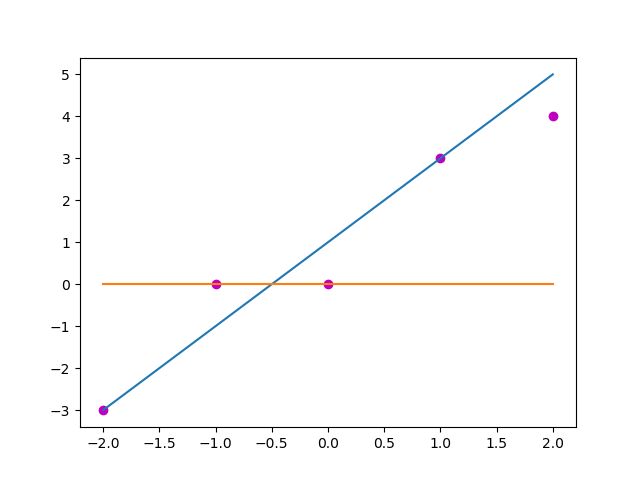
习惯上,用‘1’来代表一个神经元被激活,‘0’代表一个神经元未被激活,那预期的函数图像是这个样子的:
这个函数有什么不好的地方呢?主要的一点就是,他的梯度(导数)恒为零(个别点除外)。
想想我们说过的反向传播公式?梯度传递用到了链式法则,如果在这样一个连乘的式子其中有一项是零,结果会怎么样呢?这样的梯度就会恒为零。这个样子的函数是没有办法进行反向传播的。
那有没有什么函数可以近似实现这样子的阶梯效果而且还可以反向传播呢?常用的激活函数有哪些呢?
sigmoid函数
公式: f ( z ) = 1 1 + e − z f(z) = \frac{1}{1 + e^{-z}} f(z)=1+e−z1
反向传播:
f ′ ( z ) = f ( z ) ∗ ( 1 − f ( z ) ) f^{'}(z) = f(z) * (1 - f(z)) f′(z)=f(z)∗(1−f(z)),推导过程请参看数学导数公式。
从函数图像来看,sigmoid函数的作用是将输入限制到(0,
1)这个区间范围内,这种输出在0~1之间的函数可以用来模拟一些概率分布的情况。他还是一个连续函数,导数简单易求。
用mnist数据的例子来通俗的解释一下:
形象化的说,每一个隐藏层神经元代表了对某个笔画的感知,也就是说可能第一个神经元代表是否从图中检测到有一条像1一样的竖线存在,第二个神经元代表是否有一小段曲线的存在。但是在实际传播中,怎么表示是不是有这样一条直线或者这样一段曲线存在呢?在生活中,我们经常听到这样的对白“你觉得这件事情成功概率有多大?”“我有六成把握能成功”。sigmoid函数在这里就起到了如何把一个数值转化成一个通俗意义上的把握的表示。值越大,那么这个神经元对于这张图里有这样一条线段的把握就越大,经过sigmoid函数之后的结果就越接近100%,也就是1这样一个值,表现在图里,也就是这个神经元越兴奋(亮)。
但是这个样子的激活函数有什么问题呢?
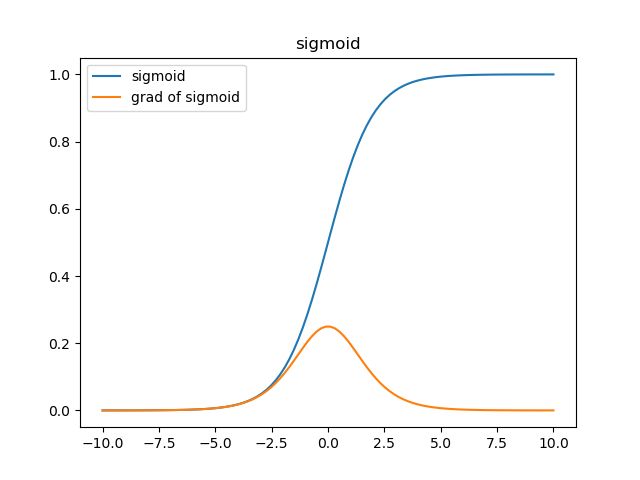
从梯度图像中可以看到,sigmoid的梯度在两端都会接近于0,根据链式法则,把其他项作为 α \alpha α,那么梯度传递函数是 α ∗ σ ′ ( x ) \alpha*\sigma'(x) α∗σ′(x),而 σ ′ ( x ) \sigma'(x) σ′(x)这时是零,也就是说整体的梯度是零。这也就很容易出现梯度消失的问题,并且这个问题可能导致网络收敛速度比较慢,比如采取MSE作为损失函数算法时。
给个纯粹数学的例子吧,假定我们的学习速率是0.2,sigmoid函数值是0.9,如果我们想把这个函数的值降到0.5,需要经过多少步呢?
我们先来做公式推导,
第一步,求出当前输入的值
1 1 + e − x = 0.9 \frac{1}{1 + e^{-x}} = 0.9 1+e−x1=0.9
e − x = 1 9 e^{-x} = \frac{1}{9} e−x=91
x = l n 9 x = ln{9} x=ln9
第二步,求出当前梯度
g r a d = f ( x ) × ( 1 − f ( x ) ) = 0.9 × 0.1 = 0.09 grad = f(x)\times(1 - f(x)) = 0.9 \times 0.1= 0.09 grad=f(x)×(1−f(x))=0.9×0.1=0.09
第三步,根据梯度更新当前输入值
x n e w = x − η × g r a d = l n 9 − 0.2 × 0.09 = l n ( 9 ) − 0.018 x_{new} = x - \eta \times grad = ln{9} - 0.2 \times 0.09 = ln(9) - 0.018 xnew=x−η×grad=ln9−0.2×0.09=ln(9)−0.018
第四步,判断当前函数值是否接近0.5
1 1 + e − x n e w = 0.898368 \frac{1}{1 + e^{-x_{new}}} = 0.898368 1+e−xnew1=0.898368
第五步,重复步骤2-3直到当前函数值接近0.5
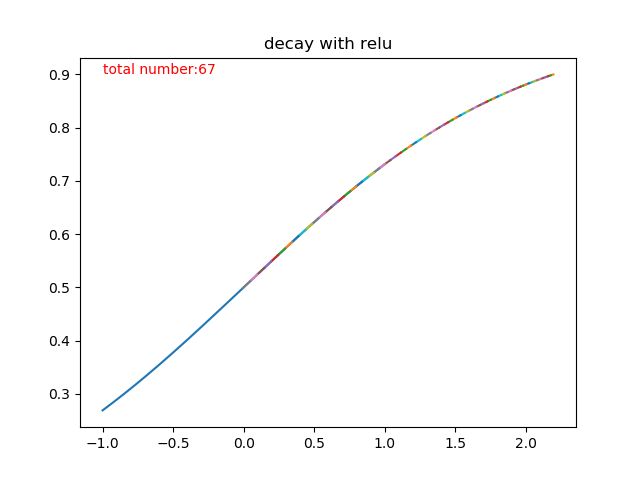
说得如果不够直观,那我们来看看图,
上半部分那条五彩斑斓的曲线就是迭代更新的过程了,一共迭代了多少次呢?根据程序统计,sigmoid迭代了67次才从0.9衰减到了接近0.5的水准。有同学可能会说了,才67次嘛,这个次数也不是很多啊!确实,从1层来看,这个速度还是可以接受的,但是神经网络只有这一层吗?多层叠加之后的sigmoid函数,因为反向传播的链式法则,两层的梯度相乘,每次更新的步长更小,需要的次数更多,也就是速度更加慢。如果还是没有反应过来的同学呢,可以先向下看relu函数的收敛速度。
此外,如果输入数据是(-1,
1)范围内的均匀分布的数据会导致什么样的结果呢?经过sigmoid函数处理之后这些数据的均值就从0变到了0.5,导致了均值的漂移,在很多应用中,这个性质是不好的。
代码思路:
放到代码中应该怎么实现呢?首先,对于一个输入进sigmoid函数的向量来说,函数的输出和反向传播时的导数是和输入的具体数值有关系的,那么为了节省计算量,可以生成一个和输入向量同尺寸的mask,用于记录前向和反向传播的结果,具体代码来说,就是:
示例代码:
class Csigmoid(object):
def __init__(self, inputSize):
self.shape = inputSize
def forward(self, image):
# 记录前向传播结果
self.mask = 1 / (1 + np.exp(-1 * image))
return self.mask
def gradient(self, preError):
# 生成反向传播对应位置的梯度
self.mask = np.multiply(self.mask, 1 - self.mask)
return np.multiply(preError, self.mask)
不理解为啥又有前向传播又有梯度计算的小伙伴请戳这里
tanh函数
形式:
f ( z ) = e z − e − z e z + e − z f(z) = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}} f(z)=ez+e−zez−e−z
f ( z ) = 2 ∗ s i g m o i d ( 2 ∗ z ) − 1 f(z) = 2*sigmoid(2*z) - 1 f(z)=2∗sigmoid(2∗z)−1
反向传播:
f ′ ( z ) = ( 1 + f ( z ) ) ∗ ( 1 − f ( z ) ) f^{'}(z) = (1 + f(z)) * (1 - f(z)) f′(z)=(1+f(z))∗(1−f(z))
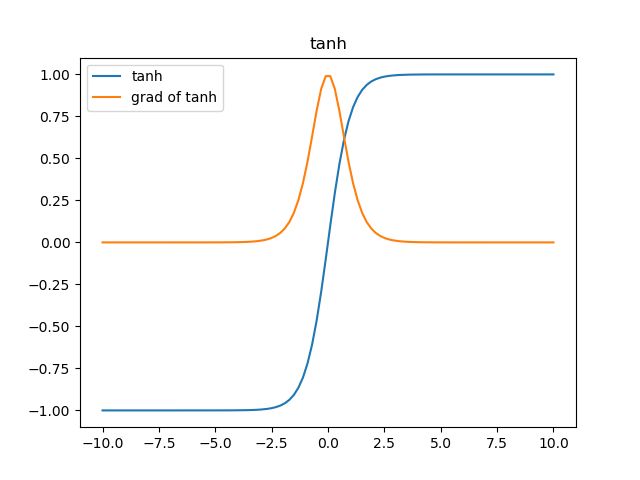
无论从理论公式还是函数图像,这个函数都是一个和sigmoid非常相像的激活函数,他们的性质也确实如此。但是比起sigmoid,tanh减少了一个缺点,就是他本身是零均值的,也就是说,在传递过程中,输入数据的均值并不会发生改变,这就使他在很多应用中能表现出比sigmoid优异一些的效果。
代码思路:
这么相似的函数没有相似的代码说不过去呀!比起sigmoid的代码,实现tanh只需要改变几个微小的地方就可以了,话不多说,直接上代码吧:
示例代码:
class Ctanh(object):
def __init__(self, inputSize):
self.shape = inputSize
def forward(self, image):
# 记录前向传播结果
self.mask = 2 / (1 + np.exp(-2 * image)) - 1
return self.mask
def gradient(self,preError):
# 生成反向传播对应位置的梯度
self.mask = np.multiply(1 + self.mask, 1 - self.mask)
return np.multiply(preError, self.mask)
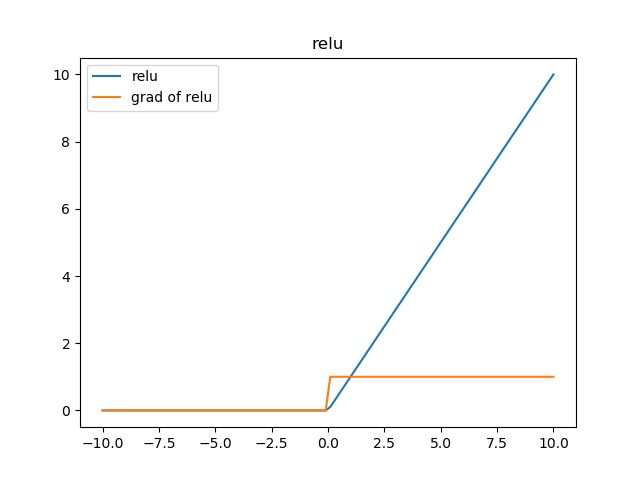
relu函数
形式:
f ( z ) = { z z ≥ 0 0 z < 0 f(z) = \begin{cases} z & z \geq 0 \\ 0 & z < 0 \end{cases} f(z)={z0z≥0z<0
反向传播:
f ( z ) = { 1 z ≥ 0 0 z < 0 f(z) = \begin{cases} 1 & z \geq 0 \\ 0 & z < 0 \end{cases} f(z)={10z≥0z<0
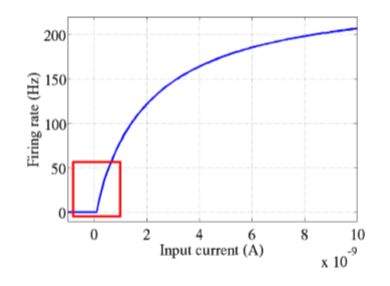
先来说说神经学方面的解释,为什么要使用relu呢?要说模仿神经元,sigmoid不是更好吗?这就要看2001年神经学家模拟出的更精确的神经元模型Deep
Sparse Rectifier Neural
Networks。简单说来,结论就是这样两幅图:
下面来解释函数图像:在输入的信号比0大的情况下,直接将信号输出,否则的话将信号抑制到0,相比较于上面两个激活函数,relu计算方面的开销非常小,避免了指数运算和除法运算。此外,很多实验验证了采用relu函数作为激活函数,网络收敛的速度可以更快。至于收敛更加快的原因,从图上的梯度计算可以看出,relu的反向传播梯度恒定是1,而sigmoid激活函数中大多数时间梯度是比1小的。在叠加很多层之后,由于链式法则的乘法特性,sigmoid作为梯度函数会不断减小反向传播的梯度,而relu可以将比梯度原样传递,也就是说,relu可以使用比较快的速度去进行参数更新。
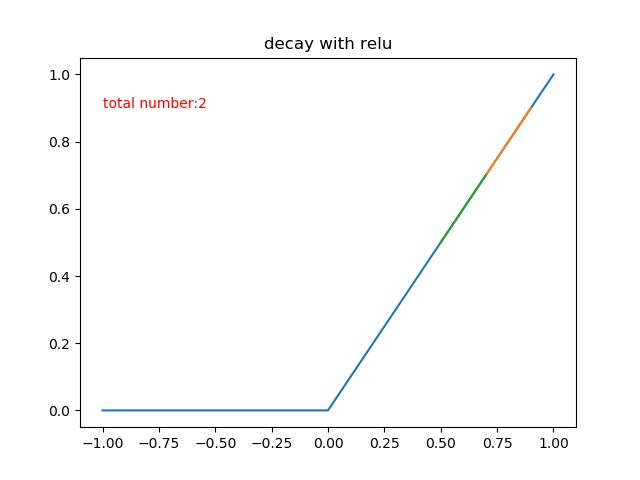
用和sigmoid函数那里更新相似的算法步骤和参数,来模拟一下relu的梯度下降次数,也就是学习率 α = 0.2 \alpha = 0.2 α=0.2,希望函数值从0.9衰减到0.5,这样需要多少步呢?
也就是说,同样的学习速率,relu函数只需要两步就可以做到sigmoid需要67步才能衰减到的程度!
但是如果回传了一个很大的梯度导致网络更新之后输入信号小于0了呢?那么这个神经元之后接受到的数据是零,对应新的回传的梯度也是零,这个神经元将不被更新,下一次输入的信号依旧小于零,不停重复这个过程。也就是说,这个神经元不会继续更新了,这个神经元“死”掉了。在学习率设置不恰当的情况下,很有可能网络中大部分神经元“死”掉,也就是说不起作用了,而这是不可取的。
代码实现:
与sigmoid类似,relu函数的前向传播和反向传播与输入的大小有关系,小于0的输入可以被简单的置成0,不小于0的可以继续向下传播,也就是将输入和0中较大的值继续传播,对输入向量逐元素做比较即可。考虑到反向传播时梯度计算也和输入有关,使用一个mask对数据或者根据数据推出的反向传播结果做一个记录也是一个比较好的选择。
示例代码:
class Crelu(object):
def __init__(self, inputSize):
self.shape = inputSize
def forward(self, image):
# 用于记录传递的结果
self.mask = np.zeros(self.shape)
self.mask[image > 0] = 1
# 将小于0的项截止到0
return np.maximum(image, 0)
def gradient(self, preError):
# 将上一层传递的误差函数和该层各位置的导数相乘
return np.multiply(preError, self.mask)
想想看,relu函数的缺点是什么呢?是梯度很大的时候可能导致的神经元“死”掉。而这个死掉的原因是什么呢?是因为很大的梯度导致更新之后的网络传递过来的输入是小于零的,从而导致relu的输出是0,计算所得的梯度是零,然后对应的神经元不更新,从而使relu输出恒为零,对应的神经元恒定不更新,等于这个relu失去了作为一个激活函数的梦想。问题的关键点就在于输入小于零时,relu回传的梯度是零,从而导致了后面的不更新。
那么最简单粗暴的做法是什么?在输入函数值小于零的时候给他一个梯度不就好了!这就是leaky
relu函数的表现形式了!
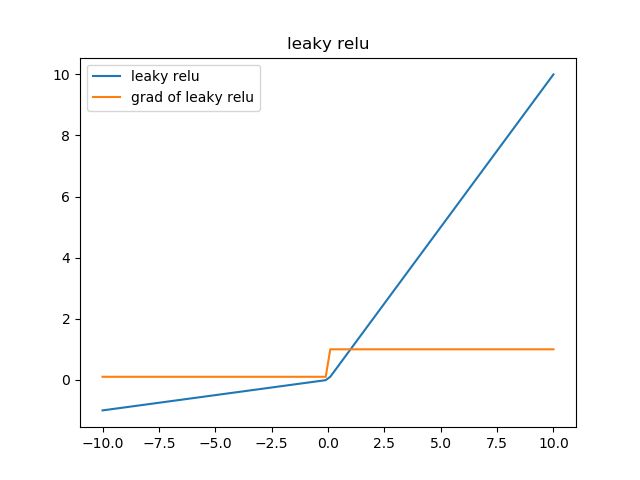
leaky relu函数
形式:
f ( z ) = { z z ≥ 0 α ∗ z z < 0 f(z) = \begin{cases} z & z \geq 0 \\ \alpha * z & z < 0 \end{cases} f(z)={zα∗zz≥0z<0
反向传播:
f ( z ) = { z 1 ≥ 0 α z < 0 f(z) = \begin{cases} z & 1 \geq 0 \\ \alpha & z < 0 \end{cases} f(z)={zα1≥0z<0
相比较于relu函数,leaky
relu同样有收敛快速和运算复杂度低的优点,而且由于给了 x < 0 x<0 x<0时一个比较小的梯度 α \alpha α,使得 x < 0 x<0 x<0时依旧可以进行梯度传递和更新,可以在一定程度上避免神经元“死”掉的问题。
示例代码:
class CleakyRelu(object):
def __init__(self, inputSize, alpha):
self.shape = inputSize
self.alpha = alpha
def forward(self, image):
# 用于记录传递的结果,按照传递公式生成对应的值
self.mask = np.zeros(self.shape)
self.mask[image > 0] = 1
self.mask[image <= 0] = self.alpha
# 将该值对应到输入中
return np.multiply(image, self.mask)
def gradient(self, preError)
# 将上一层传递的误差函数和该层各位置的导数相乘
return np.multiply(preError, self.mask)
softmax 函数
softmax函数,是大名鼎鼎的在计算多分类问题时常使用的一个函数,他长成这个样子:
ϕ ( z j ) = e z j ∑ i e z i \phi(z_j) = \frac{e^{z_j}}{\sum\limits_ie^{z_i}} ϕ(zj)=i∑eziezj
也就是说把接收到的输入归一化成一个每个分量都在 ( 0 , 1 ) (0,1) (0,1)之间并且总和为一的一个概率函数。
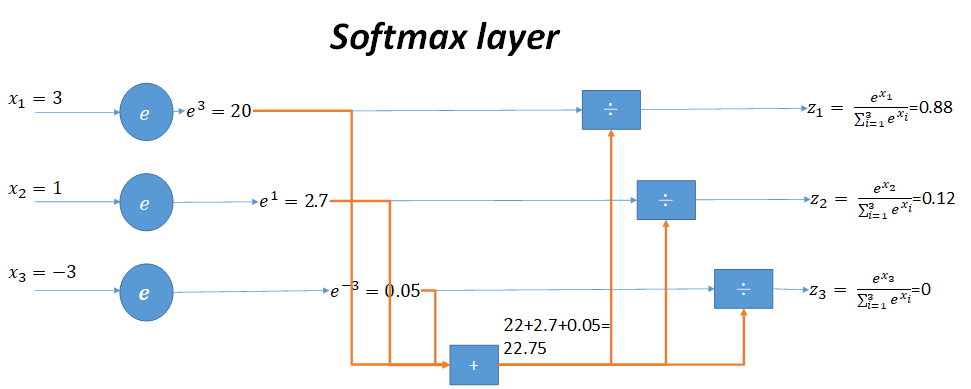
用一张图来形象说明这个过程
当输入的数据是3,1,-3时,按照图示过程进行计算,可以得出输出的概率分布是0.88,0.12,0。
试想如果我们并没有这样一个softmax的过程而是直接根据3,1,-3这样的输出,而我们期望得结果是1,0,0这样的概率分布结果,那传递给网络的信息是什么呢?我们要抑制正样本的输出,同时要抑制负样本的输出。正样本的输出和期望的差距是2,负样本1和期望的差距是0,所以网络要更加抑制正样本的结果!所以,在输出结果相对而言已经比较理想的情况下,我们给了网络一个相对错误的更新方向:更多的抑制正样本的输出结果。这显然是不可取的呀!
从继承关系的角度来说,softmax函数可以视作sigmoid的一个扩展,比如我们来看一个二分类问题,
ϕ ( z 1 ) = e z 1 e z 1 + e z 2 = 1 1 + e z 2 − z 1 = 1 1 + e z 2 e − z 1 \phi(z_1) = \frac{e^{z_1}}{e^{z_1} + e^{z_2}} = \frac{1}{1 + e^{z_2 - z_1}} = \frac{1}{1 + e^{z_2} e^{- z_1}} ϕ(z1)=ez1+ez2ez1=1+ez2−z11=1+ez2e−z11
是不是和sigmoid的函数形式非常像?比起原始的sigmoid函数,softmax的一个优势是可以用在多分类的问题中。另一个好处是在计算概率的时候更符合一般意义上我们认知的概率分布,体现出物体属于各个类别相对的概率大小。
既然采用了这个函数,那么怎么计算它的反向传播呢?
这里为了方便起见,将 ∑ i ≠ j e z i \sum\limits_{i \neq j}e^{z_i} i̸=j∑ezi记作 k k k,那么,
ϕ ( z j ) = e z j ∑ i e z i = e z j k + e z j \phi(z_j) = \frac{e^{z_j}}{\sum\limits_ie^{z_i}} = \frac{e^{z_j}}{k + e^{z_j}} ϕ(zj)=i∑eziezj=k+ezjezj
∴ ∂ ϕ ( z j ) ∂ z j = e z j ( k + e z j ) − e z j ∗ e z j ( k + e z j ) 2 = e z j k + e z j k k + e z j = s o f t m a x ( z j ) ( 1 − s o f t m a x ( z j ) ) \therefore \frac{\partial\phi(z_j)}{\partial z_j} = \frac{e^{z_j}(k + e^{z_j}) - e^{z_j} * e^{z_j}}{{(k + e^{z_j})}^2} = \frac{e^{z_j}}{k + e^{z_j}}\frac{k}{k + e^{z_j}} = softmax(z_j)(1 - softmax(z_j)) ∴∂zj∂ϕ(zj)=(k+ezj)2ezj(k+ezj)−ezj∗ezj=k+ezjezjk+ezjk=softmax(zj)(1−softmax(zj))
也就是说,softmax的梯度就是 s o f t m a x ( z j ) ( 1 − s o f t m a x ( z j ) ) softmax(z_j)(1- softmax(z_j)) softmax(zj)(1−softmax(zj)),之后将这个梯度进行反向传播就可以大功告成啦~
损失函数
作用
在有监督的学习中,需要衡量神经网络输出和所预期的输出之间的差异大小。这种误差函数需要能够反映出当前网络输出和实际结果之间一种量化之后的不一致程度,也就是说函数值越大,反映出模型预测的结果越不准确。
还是拿练枪的Bob做例子,Bob预期的目标是全部命中靶子的中心,但他现在的命中情况是这个样子的:
最外圈是1分,之后越向靶子中心分数是2,3,4分,正中靶心可以得5分。
那Bob每次射击结果和目标之间的差距是多少呢?在这个例子里面,用得分来衡量的话,就是说Bob得到的反馈结果从差4分,到差3分,到差2分,到差1分,到差0分,这就是用一种量化的结果来表示Bob的射击结果和目标之间差距的方式。也就是误差函数的作用。因为是一次只有一个样本,所以这里采用的是误差函数的称呼。如果一次有多个样本,那么就要称呼这样子衡量不一致程度的函数就要叫做损失函数了。
以做线性回归的实际值和预测值为例,若自变量x是[-2,
-1, 0, 1, 2]这样5个值,对应的期望值y是[-3, 0,
0, 3, 4]这样的值,目前预测使用的参数是(w,
b) = (2, 1), 那么预测得到的值y_
= [-3, -1, 1, 3, 5], 采用均方误差计算这个预测和实际的损失就是 ∑ i = 0 4 ( y [ i ] − y _ [ i ] ) 2 \sum_{i = 0}^{4}(y[i] - y_\_[i])^{2} ∑i=04(y[i]−y_[i])2, 也就是3。那么如果采用的参量是(0,
0),预测出来的值是[0,
0, 0, 0, 0],这是一个显然错误的预测结果,此时的损失大小就是34, 3 < 34 3 < 34 3<34, 那么(2, 1)是一组比(0,
0)要合适的参量。
那么常用的损失函数有哪些呢?
这里先给一些前提,比如神经网络中的一个神经元:
图中 z = ∑ i w i ∗ x i + b i = θ T x z = \sum\limits_{i}w_i*x_i+b_i=\theta^Tx z=i∑wi∗xi+bi=θTx, σ ( z ) \sigma(z) σ(z)是对应的激活函数,也就是说,在反向传播时梯度的链式法则中,
(1) ∂ z ∂ w i = x i \frac{\partial{z}}{\partial{w_i}}=x_i \tag{1} ∂wi∂z=xi(1)
(2) ∂ z ∂ b i = 1 \frac{\partial{z}}{\partial{b_i}}=1 \tag{2} ∂bi∂z=1(2)
(3) ∂ l o s s ∂ w i = ∂ l o s s ∂ σ ( z ) ∂ σ ( z ) ∂ z ∂ z ∂ w i = ∂ l o s s ∂ σ ( z ) ∂ σ ( z ) ∂ z x i \frac{\partial{loss}}{\partial{w_i}}=\frac{\partial{loss}}{\partial{\sigma(z)}}\frac{\partial{\sigma(z)}}{\partial{z}}\frac{\partial{z}}{\partial{w_i}}=\frac{\partial{loss}}{\partial{\sigma(z)}}\frac{\partial{\sigma(z)}}{\partial{z}}x_i \tag{3} ∂wi∂loss=∂σ(z)∂loss∂z∂σ(z)∂wi∂z=∂σ(z)∂loss∂z∂σ(z)xi(3)
(4) ∂ l o s s ∂ b i = ∂ l o s s ∂ σ ( z ) ∂ σ ( z ) ∂ z ∂ z ∂ b i = ∂ l o s s ∂ σ ( z ) ∂ σ ( z ) ∂ z \frac{\partial{loss}}{\partial{b_i}}=\frac{\partial{loss}}{\partial{\sigma(z)}}\frac{\partial{\sigma(z)}}{\partial{z}}\frac{\partial{z}}{\partial{b_i}}=\frac{\partial{loss}}{\partial{\sigma(z)}}\frac{\partial{\sigma(z)}}{\partial{z}} \tag{4} ∂bi∂loss=∂σ(z)∂loss∂z∂σ(z)∂bi∂z=∂σ(z)∂loss∂z∂σ(z)(4)
从公式 ( 3 ) , ( 4 ) (3),(4) (3),(4)可以看出,梯度计算中的公共项是 ∂ l o s s ∂ σ ( z ) ∂ σ ( z ) ∂ z = ∂ l o s s ∂ z \frac{\partial{loss}}{\partial{\sigma(z)}}\frac{\partial{\sigma(z)}}{\partial{z}} = \frac{\partial{loss}}{\partial{z}} ∂σ(z)∂loss∂z∂σ(z)=∂z∂loss。
下面我们来探讨 ∂ l o s s ∂ z \frac{\partial{loss}}{\partial{z}} ∂z∂loss的影响。由于梯度的计算和函数的形式是有关系的,所以我们会从常用损失函数入手来逐个说明。
常用损失函数
-
MSE (均方误差函数)
该函数就是最直观的一个损失函数了,计算预测值和真实值之间的欧式距离。预测值和真实值越接近,两者的均方差就越小。
-
想法来源
在给定一些点去拟合直线的时候(比如上面的例子),常采用最小二乘法,使各个训练点到拟合直线的距离尽量小。这样的距离最小在损失函数中的表现就是预测值和真实值的均方差的和。
-
函数形式:
l o s s = 1 2 ∑ i ( y [ i ] − a [ i ] ) 2 loss = \frac{1}{2}\sum_{i}(y[i] - a[i]) ^ 2 loss=21i∑(y[i]−a[i])2,
其中, a a a是网络预测所得到的结果, y y y代表期望得到的结果,也就是数据的标签, i i i是样本的序号。
-
反向传播:
∂ l o s s ∂ z = ∑ i ( y [ i ] − a [ i ] ) ∗ ∂ a [ i ] ∂ z \frac{\partial{loss}}{\partial{z}} = \sum_{i}(y[i] - a[i])*\frac{\partial{a[i]}}{\partial{z}} ∂z∂loss=i∑(y[i]−a[i])∗∂z∂a[i]
-
缺点:
和 ∂ a [ i ] ∂ z \frac{\partial{a[i]}}{\partial{z}} ∂z∂a[i]关系密切,可能会产生收敛速度缓慢的现象,以下图为例(激活函数为sigmoid)
在激活函数的两端,梯度(黄色)都会趋向于0,采取MSE的方法衡量损失,在 a a a趋向于1而 y y y是0的情况下,损失loss是1,而梯度会趋近于0,在误差很大时收敛速度也会非常慢。
在这里我们可以参考activation中关于sigmoid函数求导的例子,假定x保持不变,只有一个输入的一个神经元,权重 w = l n ( 9 ) w = ln(9) w=ln(9), 偏置 b = 0 b = 0 b=0,也就是这样一个神经元:
保持参数统一不变,也就是学习率 η = 0.2 \eta = 0.2 η=0.2,目标输出 y = 0.5 y = 0.5 y=0.5, 此处输入x固定不变为 x = 1 x = 1 x=1,采用MSE作为损失函数计算,一样先做公式推导,
第一步,计算当前误差
l o s s = 1 2 ( a − y ) 2 = 1 2 ( 0.9 − 0.5 ) 2 = 0.08 loss = \frac{1}{2}(a - y)^2 = \frac{1}{2}(0.9 - 0.5)^2 = 0.08 loss=21(a−y)2=21(0.9−0.5)2=0.08
第二步,求出当前梯度
g r a d = ( a − y ) × ∂ a ∂ z ∂ z ∂ w = ( a − y ) × a × ( 1 − a ) × x = ( 0.9 − 0.5 ) × 0.9 × ( 1 − 0.9 ) × 1 = 0.036 grad = (a - y) \times \frac{\partial{a}}{\partial{z}} \frac{\partial{z}}{\partial{w}} = (a - y) \times a \times (1 - a) \times x = (0.9 - 0.5) \times 0.9 \times (1-0.9) \times 1= 0.036 grad=(a−y)×∂z∂a∂w∂z=(a−y)×a×(1−a)×x=(0.9−0.5)×0.9×(1−0.9)×1=0.036
第三步,根据梯度更新当前输入值
w = w − η × g r a d = l n ( 9 ) − 0.2 × 0.036 = 2.161 w = w - \eta \times grad = ln(9) - 0.2 \times 0.036 = 2.161 w=w−η×grad=ln(9)−0.2×0.036=2.161
第四步,计算当前误差是否小于阈值(此处设为0.001)
a = 1 1 + e − w x = 0.8967 a = \frac{1}{1 + e^{-wx}} = 0.8967 a=1+e−wx1=0.8967
l o s s = 1 2 ( a − y ) 2 = 0.07868 loss =\frac{1}{2}(a - y)^2 = 0.07868 loss=21(a−y)2=0.07868
第五步,重复步骤2-4直到误差小于阈值
作出函数图像如图所示:
可以看到函数迭代了287次从才收敛到接近0.5的程度,这比单独使用sigmoid函数还要慢了很多。
- 交叉熵函数
这个损失函数的目的是使得预测得到的概率分布和真实的概率分布尽量的接近。两个分布越接近,那么这个损失函数得到的函数值就越小。怎么去衡量两个分布的接近程度呢?这就要用到香农信息论中的内容了。两个概率分布之间的距离,也叫做KL
Divergence,他的定义是这个形式的,给定离散概率分布P(x),
Q(x),这两个分布之间的距离是
D K L ( P ∣ ∣ Q ) = − ∑ i P ( i ) l o g ( Q ( i ) P ( i ) ) D_{KL}(P || Q) = - \sum_{i}P(i)log(\frac{Q(i)}{P(i)}) DKL(P∣∣Q)=−i∑P(i)log(P(i)Q(i))
试想如果两个分布完全相同,那么 l o g ( Q ( i ) P ( i ) ) = 0 log(\frac{Q(i)}{P(i)}) = 0 log(P(i)Q(i))=0, 也就是两个分布之间的距离是零,如果两个分布差异很大,比如一个是 P ( 0 ) = 0.9 , P ( 1 ) = 0.1 P(0)=0.9, P(1)=0.1 P(0)=0.9,P(1)=0.1,另一个是 Q ( 0 ) = 0.1 , Q ( 1 ) = 0.9 Q(0)=0.1,Q(1)=0.9 Q(0)=0.1,Q(1)=0.9,那么这两个分布之间的距离就是0.763,如果是 Q ( 0 ) = 0.5 , Q ( 1 ) = 0.5 Q(0)=0.5,Q(1)=0.5 Q(0)=0.5,Q(1)=0.5,那么距离就是0.160,直觉上来说两个分布越接近那么他们之间的距离就是越小的,具体的理论证明参看《信息论基础》,不过为什么要选用这个作为损失函数呢?
-
从最大似然角度开始说
关于最大似然,请参看
https://www.zhihu.com/question/20447622/answer/161722019
将神经网络的参数作为 θ \theta θ,数据的真实分布是 P d a t a ( y ; x ) P_{data}(y;x) Pdata(y;x), 输入数据为 x x x,那么在 θ \theta θ固定情况下,神经网络输出 y y y的概率就是 P ( y ; x , θ ) P(y;x, \theta) P(y;x,θ),构建似然函数,
L = ∑ i l o g ( P ( y i ; x i , θ ) ) L =\sum_{i}log(P(y_i;x_i, \theta)) L=i∑log(P(yi;xi,θ)),
以 θ \theta θ为参数最大化该似然函数,即 θ ∗ = a r g m a x θ L \theta^{*} ={argmax}_{\theta}L θ∗=argmaxθL。
真实分布 P ( x i ) P(x_i) P(xi)对于每一个 ( i , x i , y i ) (i, x_i, y_i) (i,xi,yi)来说均是定值,在确定 x i x_i xi情况下,输出是 y i y_i yi的概率是确定的。在一般的情况下,对于每一个确定的输入,输出某个类别的概率是0或者1,所以可以将真实概率添加到上述式子中而不改变式子本身的意义:
θ ∗ = a r g m a x θ ∑ i P d a t a ( y i ; x i ) l o g ( P ( y i ; x i , θ ) ) \theta^{*} ={argmax}_{\theta}\sum_{i}P_{data}(y_i;x_i)log(P(y_i;x_i, \theta)) θ∗=argmaxθi∑Pdata(yi;xi)log(P(yi;xi,θ))
将 D K L D_{KL} DKL展开,得到,
D K L ( P ∣ ∣ Q ) = − ∑ i P ( i ) l o g ( Q ( i ) P ( i ) ) = ∑ i P ( i ) l o g ( P ( i ) ) − ∑ i P ( i ) l o g ( Q ( i ) ) D_{KL}(P || Q) =- \sum_{i}P(i)log(\frac{Q(i)}{P(i)}) = \sum_{i}P(i)log(P(i)) - \sum_{i}P(i)log(Q(i)) DKL(P∣∣Q)=−i∑P(i)log(P(i)Q(i))=i∑P(i)log(P(i))−i∑P(i)log(Q(i))
P ( i ) P(i) P(i)代表 P d a t a ( y i ; x i ) P_{data}(y_i;x_i) Pdata(yi;xi), Q ( i ) Q(i) Q(i)代表 P ( y i ; x i , θ ) P(y_i;x_i,\theta) P(yi;xi,θ)。
上述右侧式中第一项是和仅真实分布$P(i)$有关的,在最小化$D_{KL}$过程中是一个定值,所以最小化$D_{KL}$等价于最小化$-\sum_{i}P(i)log(Q(i))$,也就是在最大化似然函数。
-
函数形式(以二分类任务为例):
l o s s = ∑ i y ( x i ) l o g ( a ( x i ) ) + ( 1 − y ( x i ) ) l o g ( 1 − a ( x i ) ) loss = \sum_{i}y(x_i)log(a(x_i)) + (1 - y(x_i))log(1- a(x_i)) loss=i∑y(xi)log(a(xi))+(1−y(xi))log(1−a(xi))
其中, y ( x i ) y(x_i) y(xi)是真实分布, a ( x i ) a(x_i) a(xi)是神经网络输出的概率分布
-
反向传播:
∂ l o s s ∂ z = ( − y ( z ) a ( z ) + 1 − y ( z ) 1 − a ( z ) ) ∗ ∂ a ( z ) ∂ z = a ( z ) − y ( z ) a ( z ) ( 1 − y ( z ) ) ∗ ∂ a ( z ) ∂ z \frac{\partial{loss}}{\partial{z}} = (-\frac{y(z)}{a(z)} + \frac{1 - y(z)}{1 - a(z)})*\frac{\partial{a(z)}}{\partial{z}} = \frac{a(z) - y(z)}{a(z)(1-y(z))}*\frac{\partial{a(z)}}{\partial{z}} ∂z∂loss=(−a(z)y(z)+1−a(z)1−y(z))∗∂z∂a(z)=a(z)(1−y(z))a(z)−y(z)∗∂z∂a(z)
在使用sigmoid作为激活函数情况下, ∂ a ( z ) ∂ z = a ( z ) ( 1 − a ( z ) ) \frac{\partial{a(z)}}{\partial{z}} = a(z)(1-a(z)) ∂z∂a(z)=a(z)(1−a(z)),也就是说,sigmoid本身的梯度和分母相互抵消,得到,
∂ l o s s ∂ z = a ( z ) − y ( z ) y ( z ) ( 1 − a ( z ) ) ∗ ∂ a ( z ) ∂ z = a ( z ) − y ( z ) \frac{\partial{loss}}{\partial{z}} = \frac{a(z) - y(z)}{y(z)(1-a(z))}*\frac{\partial{a(z)}}{\partial{z}} = a(z) - y(z) ∂z∂loss=y(z)(1−a(z))a(z)−y(z)∗∂z∂a(z)=a(z)−y(z)
在上述反向传播公式中不再涉及到sigmoid本身的梯度,故不会受到在误差很大时候函数饱和导致的梯度消失的影响。
总的说来,在使用sigmoid作为激活函数时,使用交叉熵计算损失往往比使用均方误差的结果要好上一些。但是,这个也并不是绝对的,需要具体问题具体分析,针对具体应用,有时需要自行设计损失函数来达成目标。
参考资料:
https://www.cnblogs.com/alexanderkun/p/8098781.html
https://www.zhihu.com/question/20447622/answer/161722019
《信息论基础》
点击这里提交问题与建议
联系我们: [email protected]
学习了这么多,还没过瘾怎么办?欢迎加入“微软 AI 应用开发实战交流群”,跟大家一起畅谈AI,答疑解惑。扫描下方二维码,回复“申请入群”,即刻邀请你入群。